Статья опубликована в рамках: XXI Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 17 июня 2014 г.)
Наука: Информационные технологии
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
РЕАЛИЗАЦИЯ АЛГОРИТМА ХАФФМАНА НА ЯЗЫКЕ С++ С ПОМОЩЬЮ БИНАРНЫХ ДЕРЕВЬЕВ
Горяинов Сергей Игоревич
студент 3 курса, кафедра прикладной математики Миасского филиала ЧелГУ, РФ, г. Миасс
E -mail: goryainovsergey@gmail.com
Гудков Владимир Юльевич
научный руководитель, д-р физ.-мат. наук, доцент кафедры прикладной математики Миасского филиала ЧелГУ, РФ, г. Миасс
Иванова Марина Кронидовна
научный руководитель, старший преподаватель кафедры прикладной математики Миасского филиала ЧелГУ, РФ, г. Миасс
Проблема экономного кодирования информации возникла в начале 70-х годов прошлого века, но остаётся актуальной и сегодня. В настоящее время используется ряд алгоритмов сжатия текстовых данных, таких как арифметическое кодирование, методы Зива-Лемпела, дифференциальное кодирование и др. Алгоритм Хаффмана — классический вариант адаптивного алгоритма оптимального префиксного кодирования информации с минимальной избыточностью. Как метод сжатия данных без потерь, он основан на устранении избыточности представления информации. Экономное кодирование достигается за счет представления маловероятных событий более длинными словами, чем событий с высокой вероятностью наступления. Популярность данного метода в программах сжатия данных обусловлена простотой и скоростью декодирования, а также несложной аппаратной реализацией.
В данной статье представлена реализация алгоритма Хаффмана на языке С++ с помощью полной перестройки бинарного дерева на некоторых этапах работы. В ряде источников утверждается, что подход, использующий полную перестройку бинарного дерева неэффективен, так как действия, связанные с разбором дерева, его сортировкой и новым построением, занимают большое количество времени, однако это утверждение не подкреплено соответствующими фактами. С помощью анализа текстов различной длины и количеством уникальных символов, представленных в настоящей работе, делается попытка показать, что перестройка бинарного дерева незначительно влияет на время работы программы.
Перейдём к описанию алгоритма.
На вход программы подаётся файл, содержащий текст. Затем осуществляется анализ данного текста, выполняется подсчёт частот находящихся в нём различных символов, заполнение массивов данных и их сортировка.
Следующий шаг — построение бинарного дерева. Элементы, имеющие большие частоты, располагаются справа, а элементы с меньшими частотами — слева.
При построении кода для каждого символа программа проходит по левым ссылкам узлов дерева до первого встреченного листа и обнаруживает первый элемент для объединения. После этого лист удаляется из дерева, и начинается аналогичный проход для поиска второго элемента, который после обнаружения также удаляется из дерева.
К коду всех символов первого из найденных листов добавляется единица, к коду всех символов второго листа добавляется ноль. Так, например, если символ «а» имел код 01, то, если он окажется в первом из найденных листов, код примет вид 101, если же во втором, то 001.
После нахождения двух элементов происходит их объединение в один новый элемент, причем частоты обоих суммируются, и получившееся значение присваивается новому элементу. Для нахождения места расположения образованного элемента в дереве сравниваются частоты слева и справа от текущей позиции, начиная с корневого узла. На основании этих сравнений выполняется передвижение по дереву либо влево, либо вправо. Если находится узел, частота которого равна частоте образованного элемента, происходит его вставка в текущую позицию, а найденный узел прикрепляется к вставленному слева.
Возможен случай, когда частота образованного элемента больше, чем частота узла, стоящего справа относительно текущей позиции. Если при этом выполнить действия, аналогичные действиям выше, и вставить новый элемент в дерево на место текущего, то возможна ошибка обхода дерева, в результате чего образованные коды символов будут некорректны. Для того чтобы это исправить запускается алгоритм, перестраивающий бинарное дерево. После подобной перестройки алгоритм образования новых узлов повторяется.
Программа продолжает свою работу до тех пор, пока в дереве не останется один элемент. Это означает, что все элементы были обработаны и для всех символов, которые располагались в исходном файле, были построены коды.
После этого выводится исходная строка и количество бит, занимаемых этой строкой, закодированная строка и количество бит, которые требуются для ее кодирования.
В качестве входных использовались тексты, содержащие символы русского и английского алфавитов, фрагменты кода программ и другие символы.
В таблице 1 приведены зависимости времени работы программы от длины строки и степень сжатия от числа уникальных элементов. Для анализа выбраны тексты длиной около 3000, 10000, 30000 и 50000 символов.
Таблица 1.
Зависимость времени работы программы от длины строки и степени сжатия от числа уникальных элементов
|
№ |
Длина строки (количество символов) |
Время работы программы, мс |
Количество уникальных символов |
Степень сжатия |
|
|
Тексты длиной около 3000 символов |
|||
|
1 |
3007 |
41 |
59 |
1,59 |
|
2 |
3062 |
42 |
118 |
1,49 |
|
3 |
3172 |
47 |
126 |
1,39 |
|
4 |
3039 |
42 |
118 |
1,49 |
|
5 |
2798 |
47 |
114 |
1,41 |
|
Среднее значение |
3016 |
43.8 |
|
1,5 |
|
Тексты длиной около 10000 символов |
||||
|
1 |
9498 |
103 |
150 |
1,36 |
|
2 |
9184 |
90 |
99 |
1,58 |
|
3 |
9944 |
105 |
139 |
1,44 |
|
4 |
9754 |
103 |
136 |
1,47 |
|
5 |
9867 |
98 |
95 |
1,6 |
|
Среднее значение |
9649 |
99.8 |
|
1,5 |
|
|
Тексты длиной около 30000 символов |
|||
|
1 |
28093 |
550 |
153 |
1,36 |
|
2 |
30007 |
653 |
151 |
1,5 |
|
3 |
30010 |
633 |
133 |
1,64 |
|
4 |
28469 |
563 |
140 |
1,55 |
|
5 |
28518 |
566 |
90 |
1,6 |
|
Среднее значение |
29019 |
593 |
|
1,5 |
|
Тексты длиной около 50000 символов |
||||
|
1 |
50007 |
1662 |
162 |
1,38 |
|
2 |
49100 |
1618 |
144 |
1,57 |
|
3 |
49713 |
1631 |
159 |
1,33 |
|
4 |
48669 |
1566 |
147 |
1,45 |
|
5 |
49117 |
1615 |
151 |
1,41 |
|
Среднее значение |
49321 |
1618 |
|
1,4 |
Средний коэффициент сжатия для таких текстов равен 1,5.
В таблице 2 приведена зависимость времени работы программы от длины входной строки при фиксированном количестве уникальных символов. Для анализа взяты шесть уникальных символов.
Таблица 2.
Зависимость времени работы программы от длины входной строки при фиксированном количестве уникальных символов
|
Длина строки |
Время работы, мс |
Длина строки |
Время работы, мс |
Длина строки |
Время работы, мс |
|
1125 |
33 |
6100 |
66 |
16050 |
200 |
|
1325 |
39 |
7075 |
67 |
17600 |
232 |
|
1750 |
34 |
7225 |
77 |
18825 |
263 |
|
2100 |
37 |
9000 |
84 |
20375 |
352 |
|
2375 |
38 |
9850 |
98 |
22350 |
351 |
|
2675 |
37 |
11250 |
120 |
24550 |
413 |
|
3800 |
48 |
12150 |
132 |
26525 |
477 |
|
4850 |
47 |
13225 |
150 |
28500 |
557 |
|
5375 |
62 |
14525 |
169 |
30650 |
626 |
Зависимость времени работы от длины входной строки символов представлена графически (рисунок 1), и на указанном участке соответствует функции, заданной уравнением
![]()
со средней ошибкой аппроксимации 1 %.

Рисунок 1. Зависимость времени работы программы от длины строки символов
В таблице 3 представлены результаты обработки текстов, в которых частоты символов и их общая длина постоянны, изменяется только количество уникальных символов.
Таблица 3.
Зависимость времени работы программы и степени сжатия от числа уникальных символов
|
№ |
Число уникальных символов |
Время работы, мс |
Степень сжатия |
|
1 |
10 |
50 |
2,28 |
|
2 |
15 |
58 |
2,00 |
|
3 |
20 |
54 |
1,79 |
|
4 |
25 |
49 |
1,68 |
|
5 |
30 |
50 |
1,60 |
|
6 |
35 |
55 |
1,53 |
|
7 |
40 |
50 |
1,47 |
|
8 |
45 |
59 |
1,42 |
|
9 |
50 |
62 |
1,38 |
|
10 |
55 |
57 |
1,36 |
|
11 |
60 |
49 |
1,34 |
|
12 |
65 |
57 |
1,31 |
|
13 |
70 |
50 |
1,28 |
|
14 |
75 |
55 |
1,26 |
|
15 |
80 |
52 |
1,24 |
|
16 |
85 |
62 |
1,22 |
|
17 |
90 |
55 |
1,21 |
|
18 |
95 |
63 |
1,19 |
|
19 |
100 |
58 |
1,18 |
|
20 |
105 |
58 |
1,17 |
|
21 |
110 |
63 |
1,16 |
|
22 |
115 |
61 |
1,15 |
|
23 |
120 |
54 |
1,14 |
|
24 |
125 |
65 |
1,14 |
|
25 |
130 |
64 |
1,13 |
|
26 |
135 |
57 |
1,12 |
|
27 |
140 |
68 |
1,11 |
|
28 |
145 |
64 |
1,10 |
|
29 |
150 |
74 |
1,09 |
|
30 |
155 |
64 |
1,08 |
На рисунке 2 представлена зависимость времени работы от числа уникальных символов. Изменения во времени работы программы незначительны. Данные изменения выражаются линейной функцией, которая описывается формулой ![]() . При этом средняя ошибка аппроксимации составляет 6,3 %.
. При этом средняя ошибка аппроксимации составляет 6,3 %.

Рисунок 2. Зависимость времени работы программы от числа уникальных символов
График зависимости степени сжатия от числа уникальных символов при одинаковых частотах всех символов представлен на рис. 3. Полученная линия близка к логарифмической функции
![]() ,
,
средняя ошибка аппроксимации которой составляет 3,4 %.
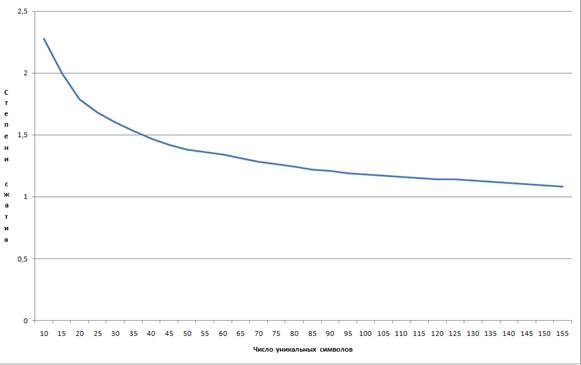
Рисунок 3.Зависимость степени сжатия от числа уникальных символов
Приблизительно аналогичные значения времени работы и степени сжатия получаются для случая, когда частоты символов взяты случайным образом при фиксированном общем количестве символов файла.
Анализируя зависимости, представленные на рисунке 1 и на рисунке 2, можно сделать вывод о том, что время, требуемое на перестройку бинарного дерева, составляет малую часть общего времени работы программы, затрачиваемого на анализ строки, на последующее ее кодирование и на вычисление степени сжатия.
График, представленный на рисунке 1, описывается уравнением ![]() . На этом графике представлена зависимость времени работы программы от длины строки входных символов. При этом число уникальных символов является константой. Это означает, что время, затрачиваемое программой на работу с бинарным деревом, приблизительно является константой, так как на него влияют и другие процессы, выполняемые операционной системой в данный момент времени. Следовательно, основная часть времени тратится на анализ входной строки и ее последующее кодирование, а время, затрачиваемое на работу с бинарным деревом, включая его перестройки, не оказывает значительное влияние.
. На этом графике представлена зависимость времени работы программы от длины строки входных символов. При этом число уникальных символов является константой. Это означает, что время, затрачиваемое программой на работу с бинарным деревом, приблизительно является константой, так как на него влияют и другие процессы, выполняемые операционной системой в данный момент времени. Следовательно, основная часть времени тратится на анализ входной строки и ее последующее кодирование, а время, затрачиваемое на работу с бинарным деревом, включая его перестройки, не оказывает значительное влияние.
График зависимости, представленные на рисунке 2, описывается линейным законом. На данном графике описывается зависимость времени работы программы от количества уникальных символов. Это означает, что время, затрачиваемое на анализ входной строки и ее кодирование, приблизительно является константой или меняется незначительно, а основная часть времени работы программы зависит от работы с бинарным деревом. Исходя из того, что время работы в этом случае подчиняется линейному закону, можно сделать вывод о том, что наличие полной перестройки бинарного дерева в ходе работы программы хоть и оказывает влияние на время работы, но, всё же, не слишком значительное. Этап работы с бинарным деревом может оказывать большое влияние на время работы программы только при очень больших количествах уникальных символов.
Список литературы:
1.Александров О.Е. Компрессия данных или измерение и избыточность информации. Метод Хаффмана: Методические указания к лабораторной работе / О.Е. Александров Екатеринбург: УГТУ–УПИ, 2000. — 36 с.
2.Кудряшов Б.Д. Теория информации: Учебник для вузов. СПб.: Питер, 2009. — 320 с.: ил. — (Серия «Учебник для вузов»).
3.Колмогоров А.Н. Теория информации и теория алгоритмов. М.: Наука, 1987. — 304 с.
4.Свирид Ю.В. Основы теории информации: Курс лекций. Мн.: БГУ, 2003. — 139 с.
5.Смирнов М.А. Обзор применения методов безущербного сжатия данных в СУБД: Рукопись. СПб.: ГУАП, 2004. — 58 с.
6.Шеннон К. Работы по теории информации и кибернетике. М.: Издательство иностранной литературы, 1963. — 825 с.
дипломов


Оставить комментарий