К  ВОПРОСУ  ОБ  ЭЛАСТИЧНОСТИ  МНОГОФАКТОРНЫХ  ЭКОНОМИЧЕСКИХ  ПОКАЗАТЕЛЕЙ

Олькин  Михаил  Артурович

студент  4  курса,  инженерный  факультет,  филиал  СКФУ,  РФ,  г.  Пятигорск

E -mail:  gorbachenkotim@mail.ru;

Тимченко  Андрей  Борисович

научный  руководитель,  канд.  экон.  наук,  кафедра  ИСиТ,  филиал  СКФУ,  РФ,  г.  Пятигорск

Известно,  что  в  экономической  теории  зависимость  между  экономическими  показателями  принято  описывать  как  функциональную,  а  для  оценки  чувствительности  функции    к  изменению    вводят  понятие  эластичности  функции  по  аргументу  [1;  2].  Обозначают  ее    или    и,  следуя  подходу  А.Маршалла,  определяют  следующим  образом

                             (1)

Смысл    следует  из  рассуждения

,  если 

·     эластичность  функции  по  аргументу  численно  равна  процентному  изменению  функции,  если  ее  аргумент  увеличить  на  1%. 

Переходя  в  (1)  к  пределу  при    вводят  точечную  эластичность

                                            (2)

и  именно  ее  используют  в  экономико  –  математических  моделях,  в  которых    задана  аналитически. 

Для  функции  многих  переменных 

,                     (3)

вводят  понятие  частных  эластичностей  показателя    по  факторам    соответственно,  т.  е.  имеют  дело  с  величинами

                                   (4)

Если  (3)  производственная  функция  (ПФ),  то  (4)  —  это  эластичности  выпуска    по  факторам  .  Так  для  классической  двухфакторной  ПФ,  описывающей  национальную  экономику  как  неструктурированное  целое 

,                                     (5)

где:  выпуск    —  ВВП, 

  —  ОПФ, 

  —  число  занятых.

Частные  эластичности  выпуска  по  фондам    и  труду    будут  равны  соответственно

,  ,                                   (6)

При  исследовании  различных  вопросов  экономической  теории,  в  частности,  при  исследовании  экономической  динамики  в  моделях  использующих  ПФ  (5)  при  произвольных  значениях  суммы  ,  возникает,  естественно,  необходимость  рассматривать  случай,  когда  все  аргументы  функции  изменяются.  В  этом  случае  полезно  ввести  понятие  полной  эластичности  функции  многих  переменных  (3),  которую  можно  считать  аналогом  полного  дифференциала  первого  порядка  этой  функции.  Непосредственно  формулу  (1)  обобщить  на  этот  случай  затруднительно,  поэтому  понятие  полной  эластичности  функции  многих  переменных  введем  следующим  образом. 

Назовем  эластичностью  (полной)  функции  многих  переменных  величину  численно  равную  процентному  изменению  этой  функции  при  увеличении  всех  ее  аргументов  на  1  %.  Обозначая  эту  величину  через    (или  ),  для  функции  (3)  запишем  на  основе  этого  определения

,

если 

                    (7)

или 

       (7а)

Теорема  1.   В  линейном  по  приращениям  аргументов  приближении  полная  эластичность  функции  многих  переменных  равна  сумме  всех  ее  частных  эластичностей

                                          (8)

Теорема  2.   Если  аргументы  функции  (3)  увеличить  соответственно  на    процентов,  то  в  линейном  приближении  процентное  изменение  функции  составит 

                        (9)

Следствие  1 .  Для  функции    и    эластичность    функции    по    в  точке    в  линейном  приближении  находится  по  формуле

,                                 (10)

где:    —  частная  эластичность    по  ,  при  , 

  —  эластичность    по    в  точке  ,  .

Следствие  2 .  Для  функций    и  ,  ,…,    полная  эластичность    функции    по  переменным  в  точке    в  линейном  приближении  находится  по  формуле 

,                                   (11)

где:      —  полная  эластичность  функции    в  точке  , 

а      —  частные  эластичности    по    при  .

Введение  понятия  полной  эластичности    функции  многих  переменных  и  утверждения  (8)  и  (9)  надеемся  сделают  многие  рассуждения  в  экономической  теории  более  простыми  и  стандартизованными. 

Естественно,  что  подобным  образом  можно  ввести  понятие  эластичности  и  для  функции  одной  переменной  ,    и  которое  в  линейном  приближении  переходит  в  (2):

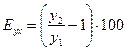,  где 

или 

,  где                                  (12)

В  линейном  приближении  получаем

  ,  тогда  ,  как  и  при  определении  (1).

Удобство  определения  (12)  проявляется  в  том,  что  оно  позволяет  обобщение  на  случай  функции  многих  переменных  при  введении  ,  тогда  как  при  определении  (1)  такого  обобщения  не  проведешь.

Кроме  указанного  обобщения  определение  (12)  позволяет  ввести  полезное  понятие  неполных  эластичностей  функции  многих  переменных,  когда  только  часть  ее  аргументов  возросла  на  1  %.

Назовем  -частичной  эластичностью  функции  (3)  многих  переменных  процентное  изменение  этой  функции  когда  ее  аргументов  ,    увеличивается  на  1%.  Обозначая  ее  ,  как  и  для  (9)  так  и  для  (12)  получим

                     (13)

Если  аргументы  меняются  на    процентов  соответственно,  то  процентное  изменение  функции  в  том  же  приближении  находится  по  формуле

  (14)

Для  полной  эластичности    легко  доказываются  следующие  ее  свойства.

Если    и  ,  то 

1)  для    ,

2)  для                                           (15)

Эти  же  свойства  справедливы  и  для    -  частичных  эластичностей.

Если  (3)  —  -факторная  производственная  функция,  то  полную  эластичность    этой  функции  естественно  называть  эластичностью  хозяйственного  механизма  (производства),  а  -частичную  эластичность  —  -факторной  эластичностью  -факторного  производства.  Для  классической  двухфакторной  ПФ  (5)  с  учетом  (8)  и  (6)  для  эластичности  хозяйственного  механизма,  получаем 

                                    (16)

Этот  результат  можно  получить  непосредственно,  используя  биномиальное  разложение  в  линейном  приближении

Учитывая,  что    можно  сказать,  что  для  ПФ  (5)  линейное  приближение,  приводящее  к  результату  (14)  дает  практически  точный  результат.

Соответственно,  если    и  ,  где    —  процент  изменения  факторов    соответственно,  то  для  (5)  аналогично  можно  получить  для  процентного  изменения  выпуска  формулу  (9):

.

Если  ,  то  имеем  экономику  с  единичной  эластичностью  производства,  в  которой  увеличение  фондов  и  труда  на  1  %  вызывает  рост  выпуска  тоже  на  1  %.  В  этом  случае  ПФ  записывают  в  виде

                                                    (17)

и  называют  функцией  Кобба-Дугласа  (ПФКД).  Именно  динамику  такой  экономики  описывает  классическая  модель  экономической  динамики  Нобелевского  лауреата  Р.  Солоу  [3]. 

Список  литературы:

1.Замков  О.О.,  Толстопятенко  А.А.,  Черемных  Ю.Н.  Математические  методы  в  экономике:  Учебник.  М.:МГУ  им.  М.В.Ломоносова,  ДНС,  1998.

2.Колемаев  В.А.  Математическая  экономика:  Учебник  для  вузов.  3-е  стереотипное  изд.  М.:  ЮНИТИ-ДАНА,  2005.

3.Solow  R.M.  Contribution  to  the  theory  of  economic  growth  //  Quarterly  Journal  of  Economics,  —  1956,  —  v.  70,  —  p.  65—94.