ПРЕДВАРИТЕЛЬНАЯ  ОБРАБОТКА  ИЗОБРАЖЕНИЙ  НА  ОСНОВЕ  ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЯ

Мифтахутдинов  Динар  Ильдусович

магистрант  2  курса,  кафедра  АСОИУ  КНИТУ-КАИ, 
РФ,  г.  Казань

E-mail:  mdi_55@mail.ru

Ризаев  Ильдус  Султанович

научный  руководитель,  канд.  техн.  наук,  профессор  каф.  АСОиУ  КНИТУ-КАИ, 
РФ,  г.  Казань

К  задачам  предварительной  обработки  можно  отнести  удаление  шумов,  сглаживание,  повышение  резкости,  подчеркивание  границ,  пороговое  преобразование  и  т.  д.

Вейвлет-преобразование  обладает  свойством  локализации  анализируемых  характеристик,  что  позволило  его  с  успехом  применять  для  фильтрации  одномерных  и  двумерных  сигналов.

Одномерное  дискретное  вейвлет-преобразование  функции  f(x)  заключается  в  ее  разложении  по  определенному  базису.  Для  формирования  вейвлет-базиса  используются  масштабирующая  функция  φ(x)  и  вейвлет-функция  ψ(x),  обладающие  специальными  свойствами.  Элементы  базиса  определяются  следующим  образом:

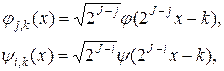      (1)

где  J  –  некоторый  фиксированный  номер,  а  j  Π [0,  J].

Функцию  f(x)  можно  представить  в  виде  ряда:

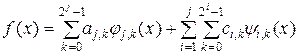,  (2)

где:  a_j,k  –  коэффициент  аппроксимации, 

c_i,k  –  коэффициент  детализации,  j  называют  уровнем  разложения  функции,  j  Π [0,  J], 

J  –  максимальный  уровень  разложения.  Причем  будем  считать,  что  уровень  0  соответствует  наиболее  детальному  приближению  с  нулевыми  коэффициентами  детализации  и  значениями  коэффициентов  аппроксимации,  равными  значениям  исходной  функции,  а  уровень  J  –  наиболее  грубому  приближению  с  единственным  коэффициентом  аппроксимации,  равным  среднему  значению  функции.  На  практике  обычно  рассматривают  J  =  log₂N,  где  N  –  число  дискретных  значений  исходной  функции  [1].

В  общем  случае  в  процедурах  вейвлет-фильтрации  функция  f(x)  представляет  собой  последовательность  дискретных  значений:

  f(x)  =  {f(0),  f(1),…,  f(N  –  1)},  (3)

где  N  –  четное  число  отсчетов.  Множество  значений  аргумента  x,  на  котором  функция  f(x)  может  принимать  отличные  от  нуля  значения,  называется  носителем  этой  функции.  Очевидно,  что  носителем  функции  является  полуинтервал  [0,  N).  Функции  φ(t)  и  ψ(t),  определяющие  вейвлет-базис,  могут  иметь  носитель  [a,  b),  отличающийся  от  носителя  функции  f(t).  В  этом  случае  необходимо  формировать  новую  функцию  =  f(x),  где  q(x)  –  функция  с  областью  определения  [0,  N)  и  областью  значений  [a,  b).  Тогда  разложение  в  ряд  будет  иметь  вид:

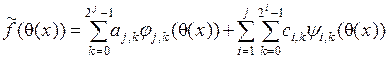  (4)

Например,  для  обработки  сигналов  часто  используют  вейвлет-базис  Хаара  с  носителем  [0,  1):

    (5)

Функция  q(x)  в  этом  случае  имеет  вид  q(x)  =  x/N.  В  дальнейшем  будем  считать,  что  носитель  функции  f(x)  совпадает  с  носителями  φ(x)  и  ψ(x).

В  результате  разложения  функции  f(x)  в  вейвлет-ряд  будет  получено  множество  коэффициентов  аппроксимации  и  детализации.  С  их  помощью  можно  представить  исходную  функцию  на  каждом  уровне  разложения  в  виде  суммы  аппроксимирующей 

  (6)

и  детализирующей 

  (7)

частей.  Задав  способ  изменения  коэффициентов  аппроксимации  и  детализации  определяют  требуемый  фильтр. 

В  качестве  базиса  для  фильтрации  сигналов  обычно  используются  ортогональные  и  биортогональные  вейвлеты,  для  которых  имеются  быстрые  алгоритмы  разложения.  К  таким  вейвлетам  относятся  вейвлеты  Хаара,  Добеши,  симмлеты,  койфлеты,  биортогональные  вейвлеты,  реверсивные  биортогональные  вейвлеты,  дискретные  вейвлеты  Мейера.

Эффективность  фильтрации  для  конкретного  сигнала  в  значительной  степени  зависит  от  выбранного  вейвлет-базиса  и  алгоритма  обработки  детализирующих  коэффициентов.  При  выборе  оптимального  вейвлет-базиса  наиболее  часто  используется  критерий  минимума  энтропи  и  распределения  квадратов  модулей  детализирующих  коэффициентов  уровней  1,  …,  J.  Критерий  выражается  следующим  образом  [3]:

         (8)

Метод,  основанный  на  этом  критерии,  подбирает  для  сигнала  такой  базис,  в  котором  распределение  значений  квадратов  его  вейвлет-коэффициентов  максимально  отличаются  от  равномерного.  Тем  самым  максимум  информации  сосредотачивается  в  минимальном  количестве  коэффициентов  разложения  [3]. 

На  основе  критерия  минимума  энтропии  строятся  методы,  позволяющие  путем  применения  того  или  иного  базиса  выявить  как  можно  более  тонкие  различия  в  структуре  сигналов,  например,  метод  когерентного  отсечения.

Использование  вейвлетов  для  удаления  шума  позволяет  применять  более  гибкие  алгоритмы.  Например,  в  настоящее  время  активно  применяются  алгоритмы  адаптивной  вейвлет-фильтрации.  Они  основаны  на  предположении  о  том,  что  шум  в  основном  сосредоточен  на  самом  высокочастотном  уровне  детализации  (уровне  1),  за  исключением  небольшого  числа  точек,  в  котором  сконцентрированы  высокочастотные  особенности  поведения  полезного  сигнала.

Помимо  сглаживания  и  удаления  шума,  т.  е.  низкочастотных  фильтров,  на  основе  вейвлет-преобразования  строятся  высокочастотные  фильтры.  Их,  например,  можно  получить  при  обнулении  коэффициенты  аппроксимации  и  сохранении  неизменными  коэффициентов  детализации.  Для  повышения  резкости  можно  увеличить  по  абсолютному  значению  коэффициенты  детализации.

Двумерное  вейвлет-преобразование  заключается  в  последовательном  выполнении  одномерного  вейвлет-преобразования  сначала  по  строкам,  а  затем  по  столбцам.  Предположим,  что  имеем  изображение  размером  N×N.  Первоначально  каждая  из  N  строк  изображения  делится  (фильтруется)  на  низкочастотную  (НЧ)  и  высокочастотную  (ВЧ)  половины.  В  результате  получается  два  изображения  размером  N×N/2.  Далее  каждый  столбец  делится  точно  также,  в  итоге  получается  четыре  изображения  размером  N/2×N/2.  Первое  из  указанных  выше  изображений  делится  аналогичным  образом  на  следующем  шаге  (уровне)  преобразования  и  т.  д.  [1].

В  заключение  отметим,  что  описанные  процедуры  фильтрации  одномерных  функций  обобщаются  на  фильтрацию  изображений.  Данный  подход  на  основе  вейвлет-фильтрации  дает  возможность  получить  оптимальное  соотношение  между  временем  и  качеством  предварительной  обработки  изображений. 

Список  литературы: 

1. Андреев  Л.П.,  Очистка  и  улучшение  качества  изображения  пространственных  распределений  в  томографии  методом  вейвлет-преобразований  //  Технические  науки.  –  2010.  –  Т.  2,  –  №  3.  –  С.  103–112.
2. Гонсалес  Р.,  Вудс  Р.  Цифровая  обработка  изображений.  –  М.:  Техносфера,  2012.  –  1104  с. 
3. Любушин  А.А.  Разведочный  анализ  свойств  временных  рядов:  учеб.  пособие.  М.:  Новое  знание,  2006.  –  47  с.