Статья опубликована в рамках: XXXVIII Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 26 января 2016 г.)
Наука: Технические науки
Секция: Электротехника
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
РАСЧЁТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ С ИСПОЛЬЗОВАНИЕМ КОМПЛЕКСНЫХ ЧИСЕЛ
Ли Геннадий Инокентиевич
студент 2 курса, кафедра Электроэнергетики и электротехники Дальневосточного федерального университета,
РФ, г. Владивосток
E-mail: li-gena-1996@mail.ru
Дмух Галина Юрьевна
научный руководитель, канд. пед. наук, доц. кафедры алгебры, геометрии и анализа ШЕН Дальневосточного Федерального Университета,
РФ, г. Владивосток
В электротехнике для расчёта сложных электрических цепей переменного тока используют метод комплексных амплитуд или комплексный метод. Что же представляет собой этот метод расчёта?
Из названия метода можно сделать вывод, что он связан с комплексными числами. Разберёмся с понятием комплексных чисел.
Комплексным числом называется выражение вида ![]() , где
, где ![]() и
и ![]() – действительные числа, а
– действительные числа, а ![]() – так называемая мнимая единица,
– так называемая мнимая единица, ![]() . Число
. Число ![]() называется действительной частью комплексного числа и обозначается
называется действительной частью комплексного числа и обозначается ![]() , а
, а ![]() – мнимой частью ,
– мнимой частью , ![]() [3, с. 218].
[3, с. 218].
Запись числа в виде ![]() называют алгебраической формой комплексного числа,
называют алгебраической формой комплексного числа, ![]() - тригонометрическая форма,
- тригонометрическая форма, ![]() - показательная форма [3, с. 220].
- показательная форма [3, с. 220].
Впервые о «мнимых числах» заговорили ещё в XVI веке, когда итальянский ученый Джироламо Кардано в 1545 году опубликовал работу, в которой, пытался решить уравнение ![]() . Решая данное уравнение, Кардано допустил существование «несуществующего» числа
. Решая данное уравнение, Кардано допустил существование «несуществующего» числа ![]() и ввёл правило умножения
и ввёл правило умножения ![]() . Однако еще три столетия математики привыкали к этим новым «мнимым» числам, время от времени пытаясь от них избавиться. Только с XIX века, после выхода в свет работ Карла Фридриха Гаусса (1777–1855), посвященных доказательству основной теоремы алгебры, комплексные числа прижились в науке. Затем было обнаружено, что многие громоздкие задачи в математике решаются гораздо проще, если пользоваться мнимыми числами.
. Однако еще три столетия математики привыкали к этим новым «мнимым» числам, время от времени пытаясь от них избавиться. Только с XIX века, после выхода в свет работ Карла Фридриха Гаусса (1777–1855), посвященных доказательству основной теоремы алгебры, комплексные числа прижились в науке. Затем было обнаружено, что многие громоздкие задачи в математике решаются гораздо проще, если пользоваться мнимыми числами.
Аналогичная ситуация произошла и в электротехнике: расчёт сложных электрических цепей переменного сводился к решению множества интегралов, а решение их становится весьма сложными. И тогда в 1893 году А.Е. Кеннели и Ч.П. Штейнметц ввели в инженерную практику комплексный метод расчёта электрических цепей.
Что же представляет собой этот метод? Из физики мы знаем, что переменным током называют ток, который с течением времени изменяется по величине и направлению. Существует несколько форм переменного тока, но более распространённым является переменный синусоидальный ток, так как в промышленных масштабах электрическая энергия производится, передается и расходуется потребителями в виде синусоидальных токов.
Синусоидальным током называется периодический переменный ток, который с течением времени изменяется по закону синуса (рисунок 1).

Рисунок 1. Кривая синусоидального тока
Напряжение и ток изменяются по гармоническому закону:
![]() [2, с. 119]
[2, с. 119]
, ![]() [2, с. 120].
[2, с. 120].
где: ![]() и
и ![]() – мгновенные значения,
– мгновенные значения,
![]() и
и ![]() – амплитудные(максимальные) значения силы тока и напряжения соответственно,
– амплитудные(максимальные) значения силы тока и напряжения соответственно,
![]() и
и ![]() – начальные фазы.
– начальные фазы.
Действующее значение силы тока и напряжения равны:

Суть комплексного метода заключается в том, что значения силы тока и напряжения записывают в комплексной форме.
Комплексное действующее значение силы тока и напряжения:
![]() ,
, ![]() [3, c. 121].
[3, c. 121].
![]() -мнимая еденица (в электротехнике не пользуются обозначением
-мнимая еденица (в электротехнике не пользуются обозначением ![]() так как буква
так как буква ![]() обозначает ток) [1, с. 77].
обозначает ток) [1, с. 77].
А комплексное значение сопротивления определяется по закону Ома:
![]() ,
,
где – модуль комплексного сопротивления, а ![]() [3, c. 123] сдвиг фаз между напряжением и током.
[3, c. 123] сдвиг фаз между напряжением и током.
Сумма и разность комплексных значений производится в алгебраической форме, а произведение и отношение в показательной форме.
Разберём данный метод на конкретном примере.
Дана схема электрической цепи (рисунок 2.) а также исходные данные (таблица 1.), определить показания Амперметра, Вольтметра и Ваттметра.
Таблица 2.
Исходные данные
|
|
|
|
|
|
|
64,25 |
100 |
880 |
19 |
40 |
50 |
![]() напряжение на активно-индуктивном элементе,
напряжение на активно-индуктивном элементе, ![]() сопротивление на резистивном элементе, L – индуктивность, С – емкость,
сопротивление на резистивном элементе, L – индуктивность, С – емкость, ![]() – сопротивление на активно-индуктивном элементе, f – частота
– сопротивление на активно-индуктивном элементе, f – частота

Рисунок 2. Последовательное соединение цепи.
РЕШЕНИЕ:
Для решения данной задачи нам необходимо знать формулу для нахождения комплексного сопротивления в цепях с последовательным соединением элементов: ![]() , где
, где ![]() [3, c. 123].
[3, c. 123].
Комплексное сопротивление на активно-индуктивном элементе ![]() :
: ![]() =
=![]() +j
+j![]() , где
, где 
Реактивное сопротивление катушки: ![]() = ω
= ω![]() , где
, где ![]() циклическая частота.
циклическая частота.
ω=![]() ,
, ![]() = ω
= ω![]() = 314·880·
= 314·880·![]() .
.
Тогда комплексное сопротивление на активно-индуктивном элементе ![]() :
:
![]() Ом.
Ом.
Сила тока на активно-индуктивном элементе определяется выражением:![]()
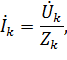
Найдем значение тока на активно-индуктивном элементе :
![]() =
=![]() A.
A.
Сила тока в последовательном соединении элементов равна:
![]() =
=![]() A.
A.
Из этого следует, что Амперметр показывает-0.23 А.
Найдем комплексное сопротивление на емкостном элементе:
![]() =
= ![]() ,
,
где ![]() реактивное сопротивление конденсатора.
реактивное сопротивление конденсатора.
Рассчитаем реактивное сопротивление конденсатора ![]() :
:
![]() =
=![]() Ом,
Ом,
отсюда ![]() Ом.
Ом.
Определим полное комплексное сопротивление:
![]() =
= Ом.
Ом.
Найдем входное напряжение цепи:
![]() В.
В.
Вольтметр показывает-40.71 В.
Найдем мощность:
![]() Вт.
Вт.
Ваттметр показывает-7.41 Вт.
По такому же принципу работают большинство современных вычислительных приборов в электротехнике. Данный пример доказывает важность комплексных чисел в электротехнике.
Список литературы:
1. Атабеков Г.И. Теоретические основы электротехники. Линейные электрические цепи: Учеб. Пособ. 7-е изд., стер. – СПб.: Издательство «Лань», 2009. – 592 с.
2. Зевеке Г.В. Основы теории цепей. Учебник для вузов. Изд. 4-е, переработанное. М., «Энергия», 1975. – 752 с. с ил.
3. Письменный Д. Конспект лекций по высшей математике, Айрис-пресс, – 2006, – 4-е изд., – 608 с.
дипломов

