МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ АВТОНОМНОГО РЕЖИМА РАБОТЫ НЕЯВНОПОЛЮСНОЙ СИНХРОННОЙ МАШИНЫ БЕЗ ДЕМПФЕРНЫХ ОБМОТОК НА ОСНОВЕ АНАЛИЗА УРАВНЕНИЙ ПАРКА - ГОРЕВА

Васильев Михаил Александрович

магистрант 1 курса, кафедра электроснабжения ВоГУ, г. Вологда

Е-mail: 

Кушнерёв Александр Андреевич

научный руководитель, канд. технических наук, доцент ВоГУ, г. Вологда

Математический анализ переходных процессов, возникающих при подаче единичного возмещения в первичном двигателе путём построения структурной схемы из типовых динамических звеньев.  Схема, будучи перенесена в программную среду, сможет дать графики переходных процессов отслеживаемых переменных.

Однолинейная схема и схема, применительно к которой будем строить модель, приведена на рис. 1.

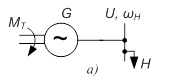
Рисунок 1 – Однолинейная схема и схема замещения генератора, работающего на автономную нагрузку

Включение в  опорную систему уравнений Парка – Горева позволяет отслеживать переходные процессы токов статора по продольной и поперечной осям.

Для облегчения задачи пренебрежём активным сопротивлением цепи статора синхронной машины (так как оно относительно мало в сравнении с остальными сопротивлениями системы), примем нагрузку в виде неизменного активного и индуктивного сопротивления.

Автономность системы обязует учитывать изменение частоты, и, как следствие реактивного сопротивления нагрузки.

С учётом вышеперечисленного получим систему уравнений:

                                   ;

                        ;

                                                              ;

                           ;

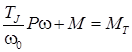  ;                   (1)

                                   ;

                                           ;

                                     ,

где: -постоянная инерции генератора; -314 рад/сек; - электромагнитный  момент на валу;  - частота вращения вала; - механический момент турбины; - синхронная ЭДС генератора по поперечной оси;  - ток ротора по поперечной оси; - КПД турбины;  - ток, напряжение и активное сопротивление обмотки возбуждения;  - напряжение на нагрузке; -постоянная времени обмотки возбуждения; - ток ротора по продольной оси; -индуктивность нагрузки;  - угол между ЭДС генератора и напряжением на нагрузке;   - определяется из выражения , где и  - синхронное и переходное сопротивления генератора по продольной оси.

Система (1) является незамкнутой. Она содержит восемь уравнений и десять неизвестных: ; ; ; ; ; ; ; ; ; . Недостающие два уравнения нужно записать для выводов машины как узловой точки с напряжением  и угловой частотой  в виде баланса активного и реактивного токов.

Построение структурной схемы для любой динамической системы по ее
уравнениям движения является задачей неоднозначной. По одним и тем же
уравнениям можно построить несколько различных по виду структурных схем.

Наиболее удобными и практичными являются схемы, раскрывающие
причинно-следственные связи.

Линеаризовав выражения по первой производной, получим выражения для приращений переменных, и заменив частные производные параметров символами  получим замкнутую систему уравнений (2), позволяющую построить искомую структурную схему, которая изображена на рис.2.

Как видно из рис. 2, синхронная машина представляет достаточно сложную систему с большим числом обратных связей, в том числе таких, которые замыкаются через нагрузку. Следует отметить, что не все связи равнозначны по своей величине. Так, связи по скоростям  и  можно считать слабыми. Однако их влияние на устойчивость может быть различной в зависимости от того, как проявляют действие другие связи. В случае автономной нагрузки генератор при отсутствии АРС эти слабые связи являются определяющими. Другое значение они имеют, если синхронная машина работает на систему бесконечной мощности. В этом случае решающее значение на устойчивость нерегулируемой машины имеет связь по углу , переходящая в связи по токам  и . Связи по скоростям тоже имеют определенное значение, особенно для машины без демпферных контуров.

                                             ;

                                                                                                                                                 ;

                            ;

                                      ;

                               ;

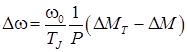;        (2)

                                                                                                                                                                                              ;

                                           ;

                                                                                                                                                    ;

                               .

Гибкая положительная связь по току  через дифференцирующее звено, отражающая влияние тока статора на ток возбуждения, представляет собой действующий в переходных режимах внутренний регулятор возбуждения машины. При увеличении продольной составляющей тока нагрузки он увеличивает возбуждение машины, оказывая существенное влияние на ее устойчивость. Следует отметить, что указанная гибкая обратная связь при определенных условиях вызывает неустойчивость, характерную для электрической части структурной схемы.

Рисунок 2 – Структурная схема неявнополюсной синхронной машины без демпферных обмоток, работающей на автономную нагрузку

Список литературы:

1. Веников, В.А. Переходные электромеханические процессы в электрических системах: учебник для электроэнергетических спец. вузов / В. А. Веников. – Москва: Высш. шк., 1985. – 536 с.

2. Жданов, П.С. Вопросы устойчивости электрических систем / П. С. Жданов. – Москва: Энергия, 1979. – 456 с.: ил.

3. Костюк, О.М. Элементы теории устойчивости энергосистем / О. М. Костюк. – Киев: Наукова думка, 1983. – 295 с.

4. Электрические системы. Математические задачи электроэнергетики: учебник для студентов вузов / под ред. В. А. Веникова. – 2-е изд., перераб. и доп. – Москва: Высш. школа, 1981.– 288 с.: ил.