Статья опубликована в рамках: XL Международной научно-практической конференции «Инновации в науке» (Россия, г. Новосибирск, 24 декабря 2014 г.)
Наука: Технические науки
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
ФРАКТАЛОПОДОБНАЯ В ВИДЕ КОВРА СЕРПИНСКОГО ОРГАНИЗАЦИЯ ПРОЦЕДУР МАЖОРИТИРОВАНИЯ ЛОГИКО-АРИФМЕТИЧЕСКИХ ОПЕРАЦИЙ В РЕКОНФИГУРИРУЕМОЙ СИСТЕМЕ КОНТРОЛЯ И ДИАГНОСТИКИ КОСМИЧЕСКОГО АППАРАТА
Савкин Леонид Васильевич
аспирант ФГУП «НПО им. С.А. Лавочкина», начальник бюро Филиала ФГУП «НПО им. С.А. Лавочкина», РФ, г. Калуга
E -mail: android4.1@mail.ru
THE MAJORITYOWNED ON THE BASIS FRAKTAL STRUCTURES OF SIERPINSKI CARPET OF LOGIC ARITHMETICAL OPERATION IN THE RECONFIGURABLE SYSTEM MONITORING AND DIAGNOSTICS OF THE SPACECRAFT
Leonid Savkin
graduate student, chief of bureau, The Branch of Federal Enterprise “Lavochkin Association”, Russia, Kaluga
АННОТАЦИЯ
Предложен способ проведения процедур мажоритирования логико-арифметических операций в реконфигурируемой системе контроля и диагностики космического аппарата. Показан пример наложения на реконфигурируемое вычислительное поле фракталоподобных структур с целью проведения процедуры мажоритирования промежуточных вычислений при формировании всех аппаратных уровней диагностической модели. Показан пример использования фракталов типа «Ковер Серпинского» в организации процедур мажоритирования вычислительных процессов.
ABSTRACT
The method majorityowned of logic arithmetical operations in the reconfigurable system monitoring and diagnostics of the spacecraft is offered. The example of superimposing fractal structures on a reconfigurable computing field is shown. The example to use fractal form «Sierpinski Carpet» in the procedures majorityowned of calculating processes is shown.
Ключевые слова: диагностическая модель; реконфигурация; мажоритирование; фрактал; реконфигурируемое вычислительное поле.
Keywords: diagnostic model; reconfiguration; majorityowned; fractal; reconfigurable computing field.
Кроме необходимого уровня контролепригодности бортовых систем космического аппарата (КА) и достаточной степени эффективности алгоритмов диагностики и контроля данных систем, существует еще целый рад факторов, определяющих то, каким будет качество бортового диагностического обеспечения КА в целом. Одними из таких факторов являются надежность функционирования системы контроля и диагностики (СКД) в процессе эксплуатации КА и достоверность информации, получаемой в ходе идентификации состояний диагностируемых бортовых систем.
С этой целью широкое распространение получили так называемые мажоритарные системы, которые реализуются сегодня во многих бортовых системах КА как программными, так и аппаратными средствами. Одним из условий, необходимых для проведения процедуры мажоритирования логико-арифметических процессов является наличие аппаратной либо программной (в зависимости от рассматриваемого типа бортовой системы) избыточности.
На рисунке 1 представлен общий пример реализации процедуры мажоритирования логико-арифметических операций, который заключается в том, что на входы идентичных по своим функциям коммутируемых логических блоков (КЛБ) поступают одинаковые сигналы ![]() .
.

Рисунок 1. Процедура мажоритирования логико-арифметических операций
Из идентичности КЛБ следует, что на их выходах должны наблюдаться также одинаковые сигналы ![]() , полученные путем одного и того же логико-арифметического преобразования сигналов, поданных на вход, при условии, что каждый из КЛБ находится в исправном состоянии. Мажоритарный орган предназначен для того, чтобы в случае возникновения сбоев и ошибок в работе КЛБ, на его выходе наблюдалась та информация, которая будет присутствовать на большинстве из выходов КЛБ.
, полученные путем одного и того же логико-арифметического преобразования сигналов, поданных на вход, при условии, что каждый из КЛБ находится в исправном состоянии. Мажоритарный орган предназначен для того, чтобы в случае возникновения сбоев и ошибок в работе КЛБ, на его выходе наблюдалась та информация, которая будет присутствовать на большинстве из выходов КЛБ.
Вероятность безотказной работы данной системы определяется тогда по формуле [4, с. 42]

где: ![]() ,
, ![]() — соответственно вероятности безотказной работы мажоритарного органа и каналов обработки информации;
— соответственно вероятности безотказной работы мажоритарного органа и каналов обработки информации;
![]() — нечетное число.
— нечетное число.
В [8] было предложено построение диагностических моделей бортовой аппаратуры КА по принципу вложенных матричных систем с многоуровневой аппаратной реконфигурацией, которую, в свою очередь, предлагалось реализовать с помощью программируемых логических интегральных схем (ПЛИС) типа FPGA, число КЛБ в которых сегодня может достигать значения нескольких миллионов единиц. Данный принцип предлагалось использовать в построении СКД на базе реконфигурируемых вычислительных систем (РВС) с целью получения максимальной гибкости алгоритмов диагностики в процессе их адаптации к сложным типам неисправностей и отказов. Кроме того, было отмечено, что возможности многоуровневой реконфигурации в СКД позволят осуществлять глубокое перестроении диагностической модели, что не всегда может быть реализовано посредством программных СКД.
Развивая идею построения реконфигурируемой СКД КА не только в отношении гибкости алгоритмов диагностики и контроля, но и в отношении надежности ее функционирования, здесь предлагается рассмотреть возможность проведения процедур мажоритирования логико-арифметических операций при формировании аппаратных уровней диагностической модели непосредственно в реконфигурируемом вычислительном поле (РВП) СКД.
Учитывая сам процесс формирования аппаратных уровней СКД, который носит чисто фрактальный характер (рисунок 2), данное свойство предлагается использовать и в процедурах мажоритирования логико-арифметических операций на всех (либо на необходимых) аппаратных уровнях диагностической модели.

Рисунок 2. Принцип формирования аппаратных уровней в реконфигурируемой СКД КА
Из данного рисунка видно, что каждая последующая аппаратная конфигурация ![]() формируемой диагностической модели, соответствующая
формируемой диагностической модели, соответствующая
![]() -му аппаратному уровню, строится на базе матричного набора
-му аппаратному уровню, строится на базе матричного набора ![]() функциональных элементов
функциональных элементов ![]() -го аппаратного уровня, что можно выразить в виде рекуррентной зависимости
-го аппаратного уровня, что можно выразить в виде рекуррентной зависимости
![]() ,
,
где: ![]() — конфигурационная функция
— конфигурационная функция ![]() -го аппаратного уровня диагностической модели;
-го аппаратного уровня диагностической модели;
![]() — матрица логико-арифметических функций КЛБ, не учитывающая топологию их параллельно-последовательных связей внутри РВП;
— матрица логико-арифметических функций КЛБ, не учитывающая топологию их параллельно-последовательных связей внутри РВП;
![]() — орграф параллельно-последовательных логико-арифметических связей между функциональными элементами
— орграф параллельно-последовательных логико-арифметических связей между функциональными элементами ![]() -го аппаратного уровня диагностической модели, которые образуют элемент
-го аппаратного уровня диагностической модели, которые образуют элемент ![]() -го аппаратного уровня.
-го аппаратного уровня.
Матрица ![]() представляет собой набор логико-арифметических функций
представляет собой набор логико-арифметических функций ![]() реализуемых посредством КЛБ, которые расположены в строке матрицы РВП
реализуемых посредством КЛБ, которые расположены в строке матрицы РВП ![]() и в столбце матрицы РВП
и в столбце матрицы РВП ![]() . Ее можно представить в следующем виде:
. Ее можно представить в следующем виде:
 ,
,
где коэффициент ![]() есть функция включения (задействования) КЛБ в образовании элемента второго аппаратного уровня, т. е.
есть функция включения (задействования) КЛБ в образовании элемента второго аппаратного уровня, т. е.

Конфигурационная функция аппаратного уровня ![]() также представляет собой матрицу вида
также представляет собой матрицу вида
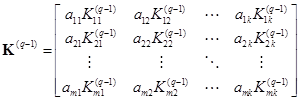 ,
,
где: элемент ![]() является уже логико-арифметической функцией элемента
является уже логико-арифметической функцией элемента ![]() -го аппаратного уровня диагностической модели;
-го аппаратного уровня диагностической модели;
коэффициент ![]() — функция включения функционального элемента
— функция включения функционального элемента ![]() -го аппаратного уровня.
-го аппаратного уровня.
На рисунке 2 представлена упрощенная структурная организация ПЛИС типа FPGA.

Рисунок 3. Структурная организация ПЛИС типа FPGA
Из данного рисунка видно, что внутренняя структура ПЛИС образована на базе двух типов матриц, топология логических и коммутационных связей между элементами которых предусматривает возможность как задействования логического блока (ЛБ) в логико-арифметическом процессе, так и возможность его отключения посредством программируемых электронных ключей (ПЭК). Поэтому не зависимо от того, сколько ПЛИС будет задействовано для реализации РВП, все РВП на первом аппаратном уровне будет представлять собой однородную структуру, совмещаемую как матрицу КЛБ, так и матрицу ПЭК.
Процесс формирования аппаратного уровня диагностической модели заключается в выделении необходимой (в функциональном отношении) области РВП, как это представлено на рисунке 4.

Рисунок 4. Выделение из РВП функционального элемента второго аппаратного уровня
Число КЛБ, включаемых в выделяемую область, может изменяться лишь при реконфигурации диагностической модели на втором аппаратном уровне ![]() , поскольку конфигурационные функции остальных аппаратных уровней носят независимый характер:
, поскольку конфигурационные функции остальных аппаратных уровней носят независимый характер:
· конфигурационная функция первого аппаратного уровня ![]() не учитывает топологию логико-арифметических связей между КЛБ вообще;
не учитывает топологию логико-арифметических связей между КЛБ вообще;
· конфигурационные функции, начиная с третьего аппаратного уровня, описывают лишь топологию связей между элементами, которые образуют данные уровни.
Таким образом, расчет вычислительного ресурса на каждом из аппаратных уровней диагностической модели носит сложный характер, как в функциональном смысле, так и в топологическом.
Вернемся к организации процедур мажоритирования логико-арифметических операций на всех аппаратных уровнях диагностической модели.
Как отмечалось, выше, ввиду того, что сам принцип образования аппаратных уровней носит фрактальный характер, то и для организации процедуры мажоритирования мы можем использовать фракталоподобные структуры, близкие по геометрическим параметрам к структуре аппаратных уровней диагностической модели.
Для данной цели из наиболее известных простых фрактальных фигур предлагается использовать «Ковер Серпинского», принцип формирования которого показан на рисунке 5.

Рисунок 5. Фрактальная фигура «Ковер Серпинского» (n — число итераций)
Итеративный метод получения фрактальной фигуры довольно прост. Базовый квадрат ![]() делится параллельными его сторонам прямыми на 9 равных по площади квадратов. Из квадрата
делится параллельными его сторонам прямыми на 9 равных по площади квадратов. Из квадрата ![]() удаляется центральный квадрат, получая при этом 8 квадратов «первого ранга». Далее аналогичная процедура проводится с каждым из квадратов «первого ранга», получая при этом множество
удаляется центральный квадрат, получая при этом 8 квадратов «первого ранга». Далее аналогичная процедура проводится с каждым из квадратов «первого ранга», получая при этом множество ![]() , которое будет состоять из 64 квадратов «второго ранга».
, которое будет состоять из 64 квадратов «второго ранга».
Пересечение членов бесконечной последовательности
![]()
и будет представлять собой фрактал типа «Ковер Серпинского».
Теперь рассмотрим рисунок 6, на котором показано, что при выделении из РВП функционального элемента второго аппаратного уровня, можно выделить средний квадрат (по вышеописанному принципу) для того, чтобы на нем была реализована функция мажоритарного органа.

Рисунок 6. Образование мажоритарной системы внутри функционального элемента второго аппаратного уровня в РВП
Оставшиеся 8 квадратов «второго ранга» мы разобьём на три изолированные друг от друга группы ![]() , которые будут выполнять роль системы с тройным мажоритированием. Таким образом, функциональный элемент второго аппаратного уровня будет представлять собой тройную мажоритарную систему, что можно записать в виде
, которые будут выполнять роль системы с тройным мажоритированием. Таким образом, функциональный элемент второго аппаратного уровня будет представлять собой тройную мажоритарную систему, что можно записать в виде
![]() , (1)
, (1)
где ![]() — процедура мажоритирования логико-арифметических операций, проводимая над набором функциональных элементов
— процедура мажоритирования логико-арифметических операций, проводимая над набором функциональных элементов ![]() .
.
Процедуру мажоритирования не обязательно проводить на каждом из аппаратных уровней ![]() диагностической модели. На рисунке 7 показан пример, когда функциональный элемент третьего аппаратного уровня
диагностической модели. На рисунке 7 показан пример, когда функциональный элемент третьего аппаратного уровня ![]() диагностической модели образован лишь матрицей элементов второго аппаратного уровня
диагностической модели образован лишь матрицей элементов второго аппаратного уровня ![]() , т. е.
, т. е.
![]() , (2)
, (2)
и
 .
.

Рисунок 7. Пример проведения неполной процедуры мажоритирования аппаратных уровней диагностической модели
В тоже время мы можем организовать проведение процедур мажоритирования логико-арифметических операций в образовании каждого аппаратного уровня диагностической модели, при этом число мажоритарных подсистем на каждом из аппаратных уровней может быть различным.
В зависимости от степени сложности диагностической модели, некоторые ее аппаратные уровне могут не проходить процедуру мажоритирования логико-арифметических операций. Параллельно с этим другие аппаратные уровни диагностической модели могут дублироваться многократно с целью прохождения процедур мажоритирования логико-арифметических операций, к примеру, для увеличения степени достоверности результатов диагностики бортовой цифровой вычислительной системы (БЦВС) при разнообразных нештатных ситуациях.
На рисунке 8 приведен пример организации процедуры мажоритирования в момент образования элемента высокого аппаратного уровня ![]() .
.
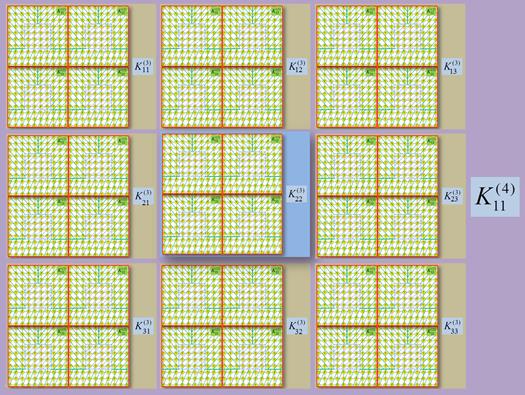
Рисунок 8. Организация процедуры мажоритирования при образовании элемента высокого аппаратного уровня (q =4)
Если на данном уровне каждая из 8 подсистем функционирует независимо, а на базе элемента ![]() реализован мажоритарный орган, то с учетом (1) и (2) конфигурационную функцию элемента четвертого аппаратного уровня можно представить в виде
реализован мажоритарный орган, то с учетом (1) и (2) конфигурационную функцию элемента четвертого аппаратного уровня можно представить в виде
![]() ,
,
причем
 .
.
Таким образом, фракталоподобную в виде ковра Серпинского организацию процедур мажоритирования логико-арифметических операций в реконфигурируемой СКД КА вполне возможно реализовать как на всех аппаратных уровнях диагностической модели, так и на выборочных.
Выводы:
1. При организации процедур мажоритирования логико-арифметических операций в СКД КА необходимо учитывать сам процесс формирования аппаратных уровней диагностической модели;
2. В зависимости от степени сложности диагностической модели операции мажоритирования можно производить как на всех аппаратных уровнях, так и на отдельных. Данное обстоятельство должно учитываться исходя как из общего вычислительного ресурса РВП, так и из его возможностей по многоуровневой реконфигурации элементов диагностической модели;
3. Максимальной эффективности от процедуры мажоритирования логико-арифметических операций можно достичь при условии обеспечения возможности реконфигурации диагностической модели на всех аппаратных уровнях, которые ее образуют.
Список литературы:
1.Алексеев А.А., Кораблев Ю.А., Шестопалов М.Ю. Идентификация и диагностика систем. М.: Издательский центр «Академия», 2009. — 352 с.
2.Евреинов Э.В. Однородные вычислительные системы, структуры и среды. М.: Радио и связь, 1981. — 208 с.
3.Евреинов Э.В., Хорошевский В.Г. Однородные вычислительные системы. Новосибирск: Наука, 1978. — 319 с.
4.Иыуду К.А. Надежность, контроль и диагностика вычислительных машин и систем: Учеб. Пособие для вузов по спец. «Вычислительные машины, комплексы, системы и сети». М.: Высш. Шк., 1989. — 216 с.
5.Каляев А.В. Многопроцессорные системы с программируемой архитектурой. М.: Радио и связь, 1984. — 240 с.
6.Каляев И.А., Левин И.И., Семерников Е.А., Шмойлов В.И. Реконфигурируемые мультиконвейерные вычислительные структуры. Ростов-н/Д.: ЮНЦ РАН, 2008. — 397 с.
7.Савкин Л.В., Новичков В.М., Ширшаков А.Е. Многоуровневая реконфигурация моделей диагностических систем как средство повышения гибкости алгоритмов диагностики и контроля бортовых систем космических аппаратов. Наукоемкие технологии в приборо- и машиностроении и развитие инновационной деятельности в вузе: материалы Всероссийской научно-технической конференции, 25—27 ноября 2014 г. Т. 2. М.: Издательство МГТУ им. Н.Э. Баумана, 2014. — С. 296—299.
дипломов


Оставить комментарий