СМЕШАННАЯ  ЗАДАЧА  ДЛЯ  УРАВНЕНИЯ  КОЛЕБАНИЯ  БАЛКИ

Рассказова  Анна  Анатольевна

студент  4  курса  Стерлитамакского  филиала  Башкирского  Государственного  Университета,  РФ,  г.  Стерлитамак

E -mail:  sunrise1008@mail.ru

Сабитова  Юлия  Камилевна

канд.  физ.-мат.х  наук,  доцент  Стерлитамакского  филиала  Башкирского  Государственного  Университета,  РФ,  г.  Стерлитамак

E-mail: 

MIXED  PROBLEM  FOR  THE  VIBRATIONS  OF  THE  BEAM

Anna  Rasskazova

4th  year  student  of  Sterlitamak  Branch  the  Bashkir  State  University,  Russia,  Sterlitamak

Julia  Sabitova

candidate  of  physico-mathematical  sciences,  associate  professor  of  Sterlitamak  Branch  the  Bashkir  State  University,  Russia,  Sterlitamak

АННОТАЦИЯ

В  данной  работе  решена  смешанная  задача  для  однородного  уравнения  поперечных  колебаний  тонкой  балки  методом  разделения  переменных.  Найдены  собственные  значения  соответствующей  спектральной  задачи  и  построены  собственные  функции.  Решение  задачи  получено  в  виде  ряда.

ABSTRACT

In  this  paper  we  solved  the  mixed  problem  for  the  homogeneous  equation  of  transverse  vibrations  of  thin  beams  by  separation  of  variables.  Found  eigenvalues  of  the  corresponding  spectral  problem  and  constructed  their  own  functions.  Solution  of  the  problem  is  obtained  in  the  form  of  a  number.

Ключевые  слова:  колебания  балки;  граничные  условия;  метод  разделения  переменных,  собственные  значения,  собственные  функции.

Keywords:  vibrations  of  the  beam;  boundary  conditions;  method  of  separation  of  variables,  eigenvalues,  eigenfunctions.

Рассмотрим  поперечные  колебания  тонкой  балки.  Главное  отличие  колебаний  балки  от  поперечных  колебаний  струны  состоит  в  том,  что  балка  оказывает  сопротивление  изгибу.  Можно  показать,  применяя  законы  механики,  что  колебания  балки,  зажатой  на  одном  конце,  описываются  уравнением 

Граничными  условиями  для  заданного  конца    является  неподвижность  балки  и  горизонтальность  касательной    а  на  свободном  концедолжны  равняться  нулю  изгибающий  момент  модуль  упругости  материала  балки,    момент  инерции  сечения  балки  относительно  своей  горизонтальной  оси  и  тангенциальная  сила    (см.  рис.  1). 

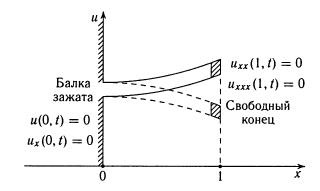
Рисунок  1.  Колебания  балки

В  уравнении  (1)  коэффициент  вычисляется  по  формуле    плотность  материала  балки,    площадь  поперечного  сечения  балки).

Для  того  чтобы  полностью  определить  движение  балки,  зажатой  на  одном  конце,  нужно  задать  начальные  условия:  начальное  отклонение  и  начальную  скорость  в  каждом  сечении  балки,  т.е.  определить

Рассмотрим  следующую  смешанную  задачу:

Будем  решать  эту  задачу  методом  разделения  переменных  в  предположении,  что  ищутся  периодические  по  времени    колебания  балки.  Полагая    и  подставляя  предполагаемую  форму  решения  в  уравнение  (2),  получим

Для  существования  периодических  по  решений  примем  .

Для  функции    получаем  задачу  о  собственных  колебаниях

при  граничных  условиях

Общее  решение  уравнения  (5)  представляется  в  виде

Из  условий    находим,  что    Отсюда  следует 

Рисунок  2.  Определение  корней  уравнения 

Граничные  условия  (6)  на  правом  конце  балки  дают  систему

Однородная  система  (относительно  неизвестных  A  и  B)  (7)  имеет  нетривиальные  решения  тогда  и  только  тогда,  когда  ее  определитель  равен  нулю:

Из  уравнения  (8)  получаем  алгебраическое  уравнение  для  вычисления  собственных  значений  задачи

Обозначив    и  воспользовавшись  равенством  ,  из  уравнения  (9)  найдем

Это  уравнение  можно  решить  графически  (рис.  2).

Корнями  уравнения  (10)  являются

Для  функции  имеем  уравнение 

Его  общее  решение  записывается  в  виде

где    и    произвольные  постоянные.

Следовательно,  «атомы»  решения  задачи  (2),  (3)  образуются  функциями 

где 

Согласно  общей  теории  задачи  Штурма  –  Лиувилля  собственные  функции    образуют  полную  ортогональную  систему  функций  на  отрезке    Тогда  решение  задачи  (2)—(4)  дается  рядом

где  коэффициенты    и  определяются  из  начальных  условий  по  формулам

Список  литературы:

1.Пикулин  В.П.,  Похожаев  С.И.  Практический  курс  по  уравнениям  математической  физики.  2-е  изд.,  стереотип.  М.:  МЦНМО,  2004.  —  208  с.

2.Сабитов  К.Б.  Уравнения  математической  физики.  М.:  ФИЗМАТЛИТ,  2013.  —  352  с.