ПРОСТРАНСТВЕННО-ДВУМЕРНЫЕ  МАТЕМАТИЧЕСКИЕ  МОДЕЛИ  ФИЛЬТРАЦИИ  ДВУХФАЗНОЙ  ЖИДКОСТИ

Григорян  Лусине  Арсеновна

старший  преподаватель  кафедры  высшей  алгебры  и  геометрии

Северо-Кавказского  федерального  университета,

РФ,  г.  Ставрополь

E -mail:  honey.lusine@mail.ru

Тимофеева  Елена  Федоровна

канд.  физ.-мат.  наук,  доцент  кафедры  высшей  алгебры  и  геометрии

Северо-Кавказского  федерального  университета,

РФ,  г.  Ставрополь

E -mail:  teflena@mail.ru

SPATIALLY  BIDIMENSIONAL  MATHEMATICAL  MODELS  OF  TWO-PHASE  LIQUID  FILTRATION

Lusine  Grigoryan

senior  Lecturer  of  Higher  Algebra  and  Geometry  Chair,

North-Caucasus  Federal  University,

Russia,  Stavropol

Elena  Timofeeva

candidate  of  Physical  and  Mathematical  Sciences,  Associate  Professor  of  Higher  Algebra  and  Geometry  Chair,  North-Caucasus  Federal  University,

Russia ,  Stavropol

АННОТАЦИЯ

Для  расчета  нефтяных  месторождений  в  терминах  «давление-водонасыщенность»  предлагается  эффективный  алгоритм  решения  задачи  фильтрации.  Численная  реализация  построенной  математической  модели  показала,  что  модифицированный  попеременно-треугольный  метод  по  числу  итераций  и  по  временным  затратам  превосходит  метод  верхней  релаксации  и  другие. 

ABSTRACT

To  calculate  the  oil  fields  in  terms  of  “pressure-water  saturation”  an  effective  algorithm  for  solving  the  problem  of  filtration  is  offered.  Numerical  realization  of  the  formed  mathematical  model  has  showed  that  a  modified  alternate-triangular  method  prevails  the  method  of  over-relaxation  and  others  according  to  the  number  of  iterations  and  time  consumption. 

Ключевые  слова:  «давление-водонасыщенность»;  модифицированный  попеременно-треугольный  метод;  математической  модели  фильтрации.

Keywords:  “pressure-water  saturation”;  modified  alternate-triangular  method;  mathematical  filtration  model. 

Ведение

Добыча  нефти  в  большинстве  случаев  происходит  при  ее  вытеснении  ее  водой  или  газом.  Этот  процесс  используется  при  естественных  режимах  эксплуатации  и  при  искусственных  методах  поддержания  пластового  давления  заводнением  или  нагнетанием  газа.  Теория  многофазной  многокомпонентной  фильтрации  служит  основой  для  расчета  таких  процессов.  Данная  работа  посвящена  одному  из  подходов  численного  моделирования  процессов  фильтрации  двухфазной  несжимаемой  жидкости  [1],  [2].

Построение  математической  модели  фильтрации  двухфазной  несжимаемой  жидкости  без  учета  капиллярных  и  гравитационных  сил.  Рассмотрим  фильтрацию  двухфазной  жидкости,  состоящей  из  нефти  (1)  и  воды  (2)  в  пористой  недеформируемой  среде,  предполагается,  что  отношение  капиллярного  давления  к  полному  гидродинамическому  падению  давления  мало.  Получим  задачу  без  учета  капиллярных  и  гравитационных  сил,  тогда  течение  двух  фаз  подчиняется  классической  модели  Баклея-Леверетта  [1].

  Как  известно,  уравнения  фильтрации  двухфазной  несжимаемой  жидкости  в  отсутствие  капиллярных  и  гравитационных  сил  имеют  вид  [4]

,                   (1)

,              (2)

водонасыщенность;    давление;относительные  фазовые  проницаемости  для  нефти  и  воды  соответственно;  мощность  пласта;  пористость  пласта;  вязкость  нефти  и  воды  соответственно;  проницаемость  пласта;    функция  Баклея-Леверетта

                                 (3)

для  задания    будем  использовать  полиномы  второго  порядка 

,                              (4)

где    предельные  значения  водонасыщенности  [2].

В  области  G  с  границей  Г  рассмотрим  граничные  условия.  Если  граница  непроницаемая,  поток  по  нормали  должен  быть  равен  нулю,  то  есть    Если  граница  проницаемая,  рассмотрим  граничные  условия  1  и  2  рода.  При  совместном  движении  фаз  ,  где    потоки  нефти  и  воды,  удовлетворяющие  условиям:    Граничные  условия  2  рода  реализуются,  когда  заданный  поток,  закачивается  на  границе  жидкости 

и  для  заданного  отбора  или  давления

Для  суммарного  потока  вытекающего  через  границу,  граничное  условие  для  насыщенности  имеет  вид

  где    водонасыщенность  на  границе  области  в  данный  момент  времени.

  —  начальное  условие.  (5)

Аппроксимация  задачи  фильтрации.  В  прямоугольной  области    рассмотрим  решение  задачи  (1)—(5).

Построим  равномерную  пространственную  сетку

неравномерную  временную  сетку

  величина  временного  шага.

Построим  консервативную  разностную  схему  неявную  по  давлению  и  явную  по  насыщенности.

  (6)

(7)

где 

определяются  из  условий

  (8)

Для  уменьшения  до  минимума  размазывания  фронта  скачка  водонасыщенности  используем  систему  разностных  уравнений  (7),  аппроксимирующих  уравнения  (2).  Система  разностных  уравнений  для  задачи  (1)—(2),  В  случае,  когда  скважина  находится  в  узле  сетки;  на  скважине  задано  забойное  давление  система  уравнений  задачи  (1)—(2),  принимает  вид  (6)—(7),  где 

              (9)

  где    —  постоянная  Эйлера,  ―радиус  скважины,  .

Погрешность  аппроксимации  схемы  (6)—(7)  имеет  вид  [4]  .  Для  произвольно  ориентированных  потоков  условия  устойчивости

    (10)

сохраняется,  если  шаг    выбирать  из  условия

  (11)

до  момента  достижения  фронта  скачка  водонасыщенности  последнего  ряда  эксплуатационных  скважин  и  по  формуле  (9)  —  после  этого  момента  [3],  [5].

Если  сетка  неравномерная    системы  разностных  уравнений  (6),  (7)  принимают  вид

  (12)

  (13)

Где    определяются  как  и  ранее,  а  по  формулам  (15)  и  (16)  соответственно.  Модифицированный  попеременно-треугольный  метод  решения  разностной  задачи  для  уравнения  давления.  Рассмотрим  модифицированный  попеременно-треугольный  метод  (МПТМ),  который  превосходит  метод  верхней  релаксации  и  другие.

Представим  систему  разностных  уравнений  (6)  в  стандартном  виде:

                 (14)

  ,  ,              (15)

,,    —  граница  прямоугольника  .

  —  равномерная  сетка,    —  множество  граничных  узлов  сетки.

Установим  связь  между  коэффициентами  уравнений  (14)  и  (6):

где    сетка  ω  —  равномерная,  покрывающая  область  G.  Установим  соответствия  между  сеточными  функциями  в  равенствах  (6)  и  (14)

или,  в  стандартных  обозначениях

Нам  потребуются  также  так  называемые  смещенные  сетки

и  скалярные  произведения

Справедливы  равенства,  которые  будут  использоваться  далее

,,, 

Запишем  сеточную  задачу  (14),  (15)  в  операторном  виде

           (16)

Схема  итерационного  двухслойного  модифицированного  попеременно-треугольного  метода  имеет  вид:

       (17)

где 

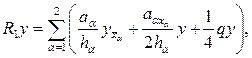                                      (18)

                             (19)

Очевидно,  что

Функция  источника  q  отлична  от  нуля  узлах  сетки,  совпадаютщих  со  скважинами.  для  реальных  сеточных  аппроксимаций  они  составляют  незначительную  долю  от  общего  числа  узлов  сетки.  Оценка  для  постоянных  входящих  в  неравенства:

,  .

При  δ=1,  параметр  ω₀  :

Поскольку  при  использовании  чебышевского  ускорения  [6]  для  числа  итераций  справедлива  оценка:

,  .

Аналогично  «стандартному»  варианту  МПТМ  имеем  оценку

.

Результаты  численных  экспериментов.

Для  проверки  качества  построенного  алгоритма  МПТМ  была  рассмотрена  модельная  задача.  Для  ее  численной  реализации  использовались  методы:  Зейделя  (МЗ),  верхней  релаксации  с  шахматным  упорядочением  (МВРШУ),  модифицированный  попеременно-треугольный  метод  (МПТМ).  Данные,  о  необходимом  числе  итераций  для  переходе  с  предыдущего  временного  на  новый  слой  по  времени  для  первых  5  временных  слоев  приведены  в  таблице  1. 

Таблица  1. 

Количество  итераций,  требуемое  для  перехода  с  предыдущего  слоя  на  новый  слой  по  времени  (сетка  400Х400  шагов)

Таблица  2. 

Количество  итераций,  требуемое  для  перехода  с  предыдущего  слоя  на  новый  слой  по  времени  (сетка  800Х800  шагов)

Результаты  численных  экспериментов  демонстрируют  преимущество  построенного  варианта  МПТМ. 

Заключение.  Построенная  разностная  схема  математической  модели  фильтрации  двухфазной  жидкости  в  относительно  тонких  однородных  по  вертикальному  направлению  пластах  позволяет  получить  корректную  оценку  в  уравнении  для  расчета  давления,  что  позволяет  использовать  минимальное  число  итераций.

Список  литературы:

1. Баренблатт  Г.И.,  Ентов  В.М.,  Зыжик  В.М.  Движение  жидкостей  и  газов  в  природных  пластах.  М.:  Недра,  1984.
2. Басниев  К.М.  Подземная  гидродинамика  /  К.М.  Басниев,  А.М.  Власов,  И.Н.  Кочина.  М.:  Наука,1986.
3. Григорян  Л.А.  Моделирование  фильтрации  двухфазной  жидкости  методом  конечных  элементов.  Вестник.  Северо-Кавказский  федеральный  университет.  Ставрополь:  СКФУ,  —  2013.  —  №  2  —  С.  13—16.
4. Григорян  Л.А.  Математическое  моделирование  задачи  разработки  нефтяных  месторождений.  /  Л.А.  Григорян,  Е.Ф.  Тимофеева//Естественные  и  математические  науки  в  современном  мире  /  Сборник  статей  по  материалам  ХVIII  международной  научно-практической  конференции.  Новосибирск:  Изд.  «СибАК»,  2014.  —  218  с.
5. 5.Коновалов  А.Н.  Задачи  фильтрации  многофазной  несжимаемой  жидкости.  Новосибирск:  Наука,1988. 
6. 6.Самарский  А.А.  Теория  разностных  схем.  М:  Наука,  1989.