РЕФРАКЦИОННЫЙ  МЕТОД  ИССЛЕДОВАНИЯ  СВЕТОВОДОВ  ТИПА  «ПАНДА» С  ЭЛЛИПТИЧНЫМИ  СЕРДЦЕВИНАМИ

Андросик  Андрей  Борисович

канд.  техн.  наук,  доцент  МГОУ,  г.  Москва

Мировицкая  Светлана  Дмитриевна

канд.  техн.  наук,  доцент  МГОУ,  г.  Москва

E-mail:  scotchwood@yandex.ru

 

REFRACTION METHOD OF INVESTIGATION OF OPTICAL FIBERS «PANDA» WITH ELLIPTICAL CORES

Andrey  Androsik

Candidate  of  Technical  Sciences,  Associate  Professor  of  MSOU,  Moscow

Svetlana  Mirovitskaya

Candidate  of  Technical  Sciences,  Associate  Professor  of  MSOU,  Moscow

 

АННОТАЦИЯ

В  работе  рассмотрен  рефракционный  метод  расчета  геометри­ческих  и  оптических  характеристик  волоконных  световодов  типа  «Панда»  с  двумя  световедущими  каналами  эллиптичной  формы.  Приведены  результаты  модельных  исследований.

ABSTRACT

This  work  proposes  a  modified  refraction  method  of  calculation  of  geometric  and  optical  characteristics  of  optical  fibers  «Panda»  with  two  waveguide  channels  of  ellipsoidal  shape.  The  results  of  the  formula  of  calculation  of  the  main  geometric  and  optical  characteristics  of  optical  fibers  are  given.  The  results  of  modelling  are  represented.

 

Ключевые  слова:  волоконный  световод;  рефракция;  геометро-оптические  характеристики.

Keywords:  optical  fiber;  refraction;  geometric  and  optical  characteristics.

В  последние  десятилетия  были  предприняты  большие  усилия  для  создания  специального  вида  одномодовых  волоконных  световодов  (ВС),  которые  проводили  только  одно  состояние  поляризации  фунда­ментальной  моды.  Подобного  рода  световоды  крайне  необходимы  как  в  когерентных  линиях  оптической  связи,  так  и  во  всевозможных  датчиках  физических  величин,  имеющих  интерферометрический  прин­цип  действия.  Для  получения  поляризующего  эффекта  в  волоконных  световодах  было  реализовано  множество  схем.  Одной  из  них  является  шлифовка  оболочки  обычного  одномодового  световода  почти  до  световедущей  жилы,  и  приведение  сошлифованной  плоской  грани  световода  в  контакт  с  двулучепреломляющим  кристаллом.  Другим  способом  является  нанесение  на  сошлифованную  грань  световода  слоя  металла.  В  [1,  с.  165]  была  предложена  математическая  модель  принципиально  однополяризационного  световода,  имеющего  большое  двулучепреломление.  Однако  такого  рода  однополяризационные  световоды  действуют  в  области  очень  малых  нормализованных  частот.  Поэтому  здесь  неизбежны  большие  потери  на  микро-  и  макроизгибах.  Также  предлагалось  использовать  обычные  анизотропные  световоды,  намотанные  в  кольца.  Существует  еще  один  способ  получения  волоконного  поляризатора  на  основе  биконической  перетяжки  свето­вода  с  высоким  двулучепреломлением.  Действие  такого  поляризатора  основано  на  механизме  взаимодействия  локальных  мод  перетянутых  световодов.  В  однополяризационных  волоконных  световодах  с  линей­ным  двулучепреломлением  разность  постоянных  распространения  двух  поляризаций  моды  можно  увеличить  либо  изменением  формы  поперечного  сечения  сердцевины  (или  оболочки)  ВС  (геометрическое  двулучепреломление),  либо  созданием  анизотропно  индуцированного  напряжения  (индуцированное  двулучепреломление).  Примером  световодов  с  большим  двулучепреломлением  являются  световоды  типа  PANDA  -polarization  maintaining  and  absorption-reducing  fiber  (ВС  с  сохранением  поляризации  и  уменьшенными  потерями  на  затухание).  Ниже  рассмотрено  решение  задачи  рефракции  узкого  пучка  на  световодах  типа  PANDA,  имеющих  не  круговые,  а  эллиптические  световедущие  сердцевины.  Проведен  анализ  и  разработка  математи­ческих  методов  расчета  картин  рассеяния  для  определения  геомет­рических  параметров  таких  BC.

Решение  задачи  рефракции  узкого  зондирующего  луча  сводится  к  следующему.  На  BC  перпендикулярно  его  оси  падает  монохрома­тическая  волна  длиной  λ.  На  расстоянии  L  от  волоконного  световода,  перпендикулярно  падающей  волне  находится  плоскость,  в  которой  осуществляется  регистрация  картины  рассеяния.

Ось  ОY1  лежит  в  плоскости  регистрации,  а  в  качестве  оси  О₁Y  выбрана  прямая,  параллельная  оси  ОY1,  проходящая  через  центр  волоконного  световода.  Ось  О₁X  проходит  через  центр  ВС,  перпендикулярно  оси  О₁Y.  Примем  точку  О₁  за  начало  координат.

Рассмотрим  путь  светового  луча,  проходящую  через  точку  с  координатами  МO(R1;YO)  .  R1  —  радиус  оболочки  ВС.  R2  —  радиус  полусфер,  которые  образуют  линзы  второго  слоя.  N1,  N2  —  показатели  преломления  слоев.  N0  —  показатель  преломления  окружающей  среды.

Проекции  луча  на  горизонтальную  ось  О₁X  обозначим  через  А_i;  проекции  луча  на  вертикальную  ось  О₁Y  обозначим  через  L_i;  отрезок  луча,  заключенный  между  границами  слоев  ВС  обозначим  через  В_i.

Луч  1  отразился  от  внешней  поверхности  BC.  Рассмотрим  путь  светового  луча,  проходящего  через  точку  AO(-R1;YO)  (рис.  1)

Данные:  О1  (0,0)  центр  окружности  (О1,  R1),  О2  (с,d)  центр  окружности  (О2,  R2),  О3  (-c,d)  центр  окружности  (О3,  R2),  О4  (c,-d)  центр  окружности  (О4,  R2),  О5  (-c,-d)  центр  окружности  (О5,  R2).  Определим  координаты  точки  М1,  как  точки  пересечения  прямой  (МО,М1)  с  окружностью  (О1,  R1).  Уравнение  прямой  (МO,М1):  y=YO.  Уравнение  окружности  (O1,R1):  x²+y²=R1²

Выразим  абсциссу  точки  М1  —  а₁:

 

 

Ордината  точки  М1  —  b₁:  b₁=YO.  Координаты  точки  М1(а₁,  b₁)

A_i  —  проекция  луча  на  горизонтальную  ось,  L_i  —  проекция  луча  на  вертикальную  ось,B_i  —  длина  луча

 

 

Исходя  из  рис.  1,  вытекают  формулы  для  определения  углов: 

 

 

уравнение  прямой  (М1,  М2):  y=k₂  x+N_{2  ,}  где  k₂  —  угловой  коэффициент  прямой,  определяющий  угол  наклона  прямой  к  оси  абсцисс;

N₂  —начальная  ордината  прямой 

 

Рисунок  1.  Траектория  луча  1

 

 

 

 

 

 

Y1  —  ордината  точки  L  точки  падения  светового  луча  на  плоскость  регистрации:  Y1=YO+L_{2  .}  Интенсивность  определяем  по  следующей  формуле: 

 

 

  —  коэффициент  отражения. 

Луч  2,  луч,  проходящий  через  однородный  BC  без  отражений  (рис.  2).

Точка  М1  получается  аналогично  точке  М1  луча  1.  Координаты  М1(a₁  ,  b₁):

 

По  закону  Снелля: 

 

 

 

Точка  М2  —  точка  выхода  светового  луча  из  ВС  через  переднюю  полусферу.

Уравнение  прямой  (М1М2):

 

 

М2  —  точка  пересечения  (М1М2)  с  окружностью  (O1,  R1).  Выведем  формулы  для  определения  координат  точки  (a,  b)  пересечения  прямой,  уравнение  которой  y=kx+N  и  окружности  с  центром  в  точке  O_i  (c,d)  и  радиусом  R; 

Уравнение  окружности  (x-c)²+(y-d)²  =  R²  .  Подставив  ординату  прямой  в  уравнение  окружности:  (x-c)²+(kx+N-d)²  =  R²,  и  преобразовав

 

 

можно  получить  квадратное  уравнение  вида 

Решаем  данное  уравнение: 

Корни  уравнения  можно  найти  по  формуле:

 

 

Получаем

 

 

 

Преобразуем  (т.  к.  a=x)

 

 

Отсюда  видно,  что  абсцисса  точки  пересечения  прямой  y=kx+N  и  окружности    функционально  зависит  от  k,  N,  c,  d,  R

 

 

Рисунок  2.  Траектория  луча  2

Подставляя  абсциссу  точки  в  уравнение  прямой  y=kx+N,  получим  ординату  b=ka+N  , 

Величина  b  функционально  зависит  от  k,  N,  а: 

Координаты  точки  М2  (a₂,  b₂):      

 

 

горизонтальная  проекция  луча 

вертикальная  проекция  луча 

длина  луча  (М1М2) 

Определим  угол  падения  луча  в  точке  .    —  угол  между  прямыми  (М1М2)  и  (О1М2).  Уравнение  прямой  (О1М2)  получим  как  уравнение  прямой,  проходящей  через  две  точки  с  координатами  О1  (0,0);  М2  (а₂,  b₂)

 

 

 

Приведем  полученное  уравнение  к  уравнению  с  угловым  коэффициентом: 

  ;  угловой  коэффициент  прямой  (О1  М2):  ,  угловой  коэффициент  прямой  (М1М2):    .  Угол  между  двумя  прямыми  определим  по  формуле: 

 

 

 

По  закону  Снелля: 

Определим  ординату  точки  М3  падения  луча  на  плоскость  регистрации,  т.  е.  точку  пересечения  луча  с  прямой  x=R1+L.  Уравнение  прямой  (М2М3):  y=k₃x+N₃ 

 

 

 

горизонтальная  проекция  луча  ,  вертикальная  проекция  луча      

 

  .

 

Луч  3,  прошедший  в  однослойный  ВС,  отразившийся  от  внутренней  поверхности  и  вышедший  наружу  (рис.3). 

До  точки  М2  прохождение  луча  совпадает  с  прохождением  луча  2.

 

 

В  точке  М2  луч  отражается  от  внутренней  поверхности. 

 

 

H  —  точка  выхода  луча  из  ВС  через  заднюю  полусферу.

Уравнение  (М2М3):

 

 

Определим  угол  падения  луча  в  точке  М3(a₃,  b₃)    —  угол  между  прямыми  (М2М3)  и  (O1М3).

Уравнение  прямой  (O1М3)  получим,  как  уравнение  прямой,  проходящей  через  две  точки  О1  (0,0)  и  М3(a₃,  b₃) 

 

 

 

Угол  преломления  луча  при  выходе  из  BC  определим  по  закону  Снелля: 

 

 

Уравнение  (М3М4):

 

 

М4  точка  пересечения  (М3М4)  с  прямой

 

 

 

 

 

 

Рисунок  3.  Траектория  луча  3

 

Луч  4,  проходящий  в  ВС,  и,  отразившийся  снаружи  от  поверх­ности  второго  слоя,  образованного  сферой  с  центром  О₂  (с,d)  и  радиусом  R2  и  вышедший  наружу  (рис.  4).  До  точки  М1  прохождение  луча  совпадает  с  лучом  2. 

 

 

 

Точка  М2  —  точка  пересечения  прямой  (М1М2)  с  окружностью  (О₂,  R₂):  М2  (а₂,  b₂).  Уравнение  прямой  (М1М2): 

 

 

 

 

Рисунок  4.  Траектория  луча  4

 

В  точке  М2  луч  отразился  от  наружной  поверхности  и  вышел  из  ВС  в  точке  М3.

  —  угол  падения  в  точке  М2.    —  угол  между  прямыми  (М1М2)  и  (О2,М2)

Уравнение  прямой  (О2,М2): 

угловой  коэффициент  (О2,М2): 

 

  ,    (рис.  4)

 

Уравнение  прямой  (М2М3):

 

 

М3  —  точка  пересечения  прямой  (М2М3)  с  окружностью  (О₁,R₁):  М3(a₃,b₃)

 

 

 

Определение  угла  падения  в  точке  М3  —  (угол  между  прямыми  (М2М3)  и  (О1,М3)). 

 

 

 

 

 

 

 

По  закону  Снелля:

 

 

Уравнение  прямой  (М3М4)

 

 

Координаты  М4(a₄,b₄):

 

 

Луч  5,  прошедший  в  ВС,  прошедший  без  отражений  линзу  второго  слоя  и  вышедший  наружу  (рис.  5).  До  точки  М2  прохождение  луча  совпадает  с  прохождением  луча  4.

 

По  закону  Снелля:

 

 

Уравнение  прямой  (М2М3)

 

 

 

Точка  М3  —  точка  пересечения  (М2М3)  с  окружностью  (O₃,R₂):  М3(a₃,  b₃)

 

 

 

Определение  угла  падения  в  точки  М3  —  .    —  угол  между  прямыми  (М2М3)  и  (О3  М3)

 

По  закону  Снелля:

 

 

Уравнение  прямой  (М3М4):

 

 

Координаты  точки  М4  (a₄,  b₄):

 

 

 

 

Рисунок  5.  Траектория  луча  5

Вычислим  угол  падения  в  точке  М4  — 

  —  угол  между  прямыми  (М3М4)  и  (O1М4)

 

 

 

  .

 

Луч  5  попадает  на  плоскость  регистрации  в  точке  М5.  Уравнение  прямой  (М4М5):

 

 

Координаты  М5  (a₅,b₅):

 

 

 

 

Ниже  приведены  результаты  модельных  исследований  при  изме­нении  линейного  и  углового  отклонения  зондирующего  пучка  в  зависимости  от  изменения  геометрических  и  оптических  параметров  световода  и  наличия  иммерсионной  жидкости,  сглаживающей  переход  пучка  из  внешней  среды  в  оболочку  [2,  с.  59].

Результаты  расчета  координаты  YL  и  угла  F  зондирующего  пучка  для  базового  варианта  представлены  на  рис.  6.

 

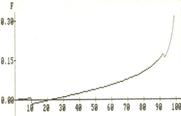
Рисунок  6.  Базовый  вариант  расчета:  R1=100  мкм,  R2=80  мкм,  N0=1,3999,  N1=1,4500,  N2=1,4800,  A2=10,  B2=10

 

При  изменении  параметра  В2  от  10  до  90  с  шагом  10  наблюдается  трансформация  пика,  обусловленная  особенностями  прохождения  пучка  в  линзу  второго  слоя  (рис.  7).  С  увеличением  В2  уменьшается  расстояние  между  характерными  пиками,  что  свидетельствует  об  уменьшении  размеров  линзы  второго  слоя.  Вычисления  проводи­лись  при  N0=1,3999,  N1=1,4500,  N2=1,4800,  R1=100  мкм,  A2=10.  При  показателя  преломления  N1<N2  линза  является  фокусирующей.  Чем  меньше  размеры  линзы,  тем  ярче  заметны  ее  фокусирующие  свойства  на  графике  углового  положения  зондирующего  пучка.

 

R2=70  мкм,  B2=20

 

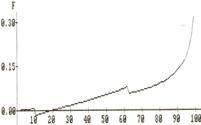
R2=50  мкм,  B2=40

R2=30  мкм,  B2=60

 

R2=10  мкм,  B2=80

Рисунок  7.  Результаты  моделирования  при  изменении  параметра  В2

 

Список  литературы:

1. Андросик  А.Б.,  Мировицкая  С.Д.  Особенности  рефракции  пучка  на  слоистых  световодах  //  Сб.научных  трудов.  —  Ставрополь,  2012.—  С.  161—171.

2. Лазарев  Л.П.,  Мировицкая  С.Д.  Контроль  геометрических  и  оптических  параметров  волокон.  —  М.:  Радио  и  связь,  1988.  —  280  с.