Статья опубликована в рамках: XXIX Международной научно-практической конференции «Инновации в науке» (Россия, г. Новосибирск, 29 января 2014 г.)
Наука: Математика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
СТРУКТУРА РЕШЕНИЙ НЕЛИНЕЙНОЙ СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ОТКЛОНЕНИЕМ И ПАРАМЕТРОМ
Свирилина Татьяна Викторовна
канд. физ.-мат. наук, доцент кафедры «Высшая математика и физика» ФГБОУ ВПО «Московский государственный университет пищевых производств», РФ, г. Москва
STRUCTURE OF DECISIONS OF NONLINEAR SYSTEM OF THE DIFFERENTIAL EQUATIONS WITH THE DEVIATION AND PARAMETER
Tatyana Svirilina
candidate of Science, associate professor "The higher mathematics and physics" FGBOU VPO "Moscow State University food productions", Russia Moscow
АННОТАЦИЯ
Доказана теорема об условии представления решения системы дифференциальных уравнений с отклонением и параметром в виде суммы двух слагаемых, одно из которых линейно относительно начального значения решения, другое — бесконечно малая величина более высокого порядка относительно начального значения и параметра.
ABSTRACT
The theorem of a condition of submission of the decision of system of the differential equations with a deviation and parameter in the form of the sum of two composed, one of which linearly rather initial value of the decision, another — the infinitesimal size of higher order of rather initial value and parameter is proved.
Ключевые слова: система дифференциальных уравнений; отклонение; параметр; двухточечная краевая задача.
Keywords: system of the differential equations; deviation; parameter; point-to-point regional task.
Рассмотрим нелинейную систему дифференциальных уравнений с отклонением ![]() и параметром
и параметром ![]() .
.
![]() . (1)
. (1)
Введем следующие обозначения: ![]() ,
, ![]() ,
, ![]() ,
, ![]() , где
, где ![]() —
— ![]() -мерный вектор,
-мерный вектор, ![]() — вектор-функция,
— вектор-функция, ![]() — матрица, зависящая от
— матрица, зависящая от ![]() .
.
Теорема. Пусть выполнены следующие условия: 1) ![]() на множестве
на множестве ![]() , 2)
, 2) ![]() ,
, 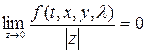 равномерно относительно
равномерно относительно ![]() , где
, где ![]() , 3) функция
, 3) функция ![]() допускает только конечное число выходов за пределы сегмента
допускает только конечное число выходов за пределы сегмента ![]() (определение в статье [1, с. 71]). Тогда решение
(определение в статье [1, с. 71]). Тогда решение ![]() ,
, ![]() , системы (1) представимо в виде
, системы (1) представимо в виде ![]() , где
, где ![]() — фундаментальная матрица решений системы
— фундаментальная матрица решений системы ![]() ,
, ![]() .
.
Доказательство. Рассмотрим линейную неоднородную систему дифференциальных уравнений
![]() . (2)
. (2)
Решение ![]() системы (1) с начальным условием
системы (1) с начальным условием ![]() является решением системы (2). А решение
является решением системы (2). А решение ![]() системы (2) с начальным условием
системы (2) с начальным условием ![]() является решением системы (1), и справедливо равенство
является решением системы (1), и справедливо равенство ![]() для любого
для любого ![]() . Тогда решение системы (1) можно представить в виде
. Тогда решение системы (1) можно представить в виде
 (3)
(3)
Так как матрица ![]() непрерывная, то матрица
непрерывная, то матрица ![]() также непрерывная, следовательно, матрицы
также непрерывная, следовательно, матрицы ![]() ,
, ![]() ограничены на сегменте
ограничены на сегменте ![]() , т. е. существуют
, т. е. существуют ![]() и
и ![]() . Пусть
. Пусть ![]() . Докажем, что второе слагаемое в правой части равенства (3) есть
. Докажем, что второе слагаемое в правой части равенства (3) есть ![]() , где
, где ![]() .
.
Так как функция ![]() является решением системы (1), то справедливо равенство
является решением системы (1), то справедливо равенство
![]() .
.
Представим вектор-функцию ![]() в следующем виде:
в следующем виде: ![]() , где
, где ![]() ,
, ![]() — непрерывная на
— непрерывная на ![]()
![]() –матрица. Интегрируя предыдущее равенство, получим
–матрица. Интегрируя предыдущее равенство, получим
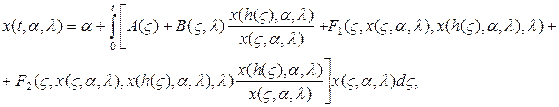
откуда

Обозначим

Тогда по неравенству Гронуолла-Беллмана имеем ![]() , откуда
, откуда  . Следовательно, величина
. Следовательно, величина  ограничена, то есть существует число
ограничена, то есть существует число ![]() такое, что
такое, что  . Величина
. Величина  тоже ограничена. Действительно, поскольку функция
тоже ограничена. Действительно, поскольку функция  непрерывна на сегменте
непрерывна на сегменте ![]() , следовательно, она ограничена на нем, то есть существует число
, следовательно, она ограничена на нем, то есть существует число ![]() такое, что выполняется неравенство
такое, что выполняется неравенство 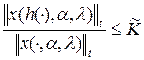 . Тогда получим
. Тогда получим
 .
.
Поскольку  , то для любого
, то для любого ![]() существует число
существует число ![]()
![]() , такое, что при условии
, такое, что при условии ![]() выполняется
выполняется  . Тогда
. Тогда  . Заметим, что
. Заметим, что ![]() при любом
при любом ![]() . Тогда величина
. Тогда величина  ограничена, то есть существует число
ограничена, то есть существует число ![]() такое, что
такое, что  . Возьмем
. Возьмем ![]() , где
, где ![]() – произвольное число. Тогда
– произвольное число. Тогда  . Следовательно, для любого
. Следовательно, для любого ![]() ,
, ![]() , имеем
, имеем

По условию ![]() и матрица
и матрица ![]() непрерывна на
непрерывна на ![]() , тогда
, тогда ![]() , то есть существует число
, то есть существует число ![]() такое, что при
такое, что при ![]() выполняется
выполняется  .
.
Тогда
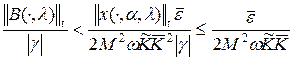 .
.
Следовательно, для любого ![]() ,
, ![]() , для любого
, для любого ![]() ,
, ![]() , имеем
, имеем 
Таким образом,
 , и решение системы (1)
, и решение системы (1) ![]() , удовлетворяющее начальному условию
, удовлетворяющее начальному условию ![]() , представимо в виде
, представимо в виде ![]() .
.
Теорема доказана.
Список литературы:
1.Свирилина Т.В. Теорема о существовании, единственности и непрерывной зависимости решения от начальных данных и параметра системы дифференциальных уравнений с отклонением // Известия РАЕН. Дифференциальные уравнения. — 2005. — № 9. — С. 70—75.
дипломов


Оставить комментарий