АНАЛИЗ  ТОЧНОСТИ  ИНТЕГРИРОВАНИЯ  ФУНКЦИЙ  ОТКЛОНЕНИЯ  ПРИ  ЭРМИТОВОЙ  ИНТЕРПОЛЯЦИИ

Андросик  Андрей  Борисович

канд.  техн.  наук,  доцент  МГОУ,  г.  Москва

Воробьев  Сергей  Андреевич

канд.  техн.  наук,  профессор  МГОУ,  г.  Москва

Мировицкая  Светлана  Дмитриевна

Канд.  техн.  наук,  доцент  МГОУ,  г.  Москва

E-mail: 

ACCURACY  OF  INTEGRATION  ANALYSIS  OF  DEVIATION  FUNCTIONS  WHEN  HERMITIAN  INTERPOLATION

Andrey  Androsik

candidate  of  Science,  associate  professor  of  Moscow  State  Open  University,  Moscow

Sergey  Vorobyev

candidate  of  Science,  professor  of  Moscow  State  Open  University,  Moscow

Svetlana  Mirovitskaya

candidate  of  Science,  associate  professor  of  Moscow  State  Open  University,  Moscow

АННОТАЦИЯ

Решена  задача  интегрирования  функции  отклонения  светового  пучка,  зондирующего  волоконный  световод  с  использованием  эрмитовой  интерполяции.  Решение  получено  с  использованием  аппарата  сплайн-функций.  Приведены  оценки  точности  интерполяции. 

ABSTRACT

The  integration  problem  of  a  deviation  function  of  a  light  beam  probing  a  fiber-light  guide  using  Hermitian  interpolation  has  been  solved.  The  solution  has  been  made  with  a  help  of  spline  function  means.  Estimations  about  interpolation  accuracy  are  given. 

Ключевые  слова:  эрмитова  интерполяция,  волоконный  световод,  функции  отклонения,  рефракция.

Keywords:  Hermitian  interpolation;  fiber-light  guide;  deviation  functions;  refraction.

В  ряде  работ  [1,  с.  14,  2,  с.  227]  показано,  что  по  сравнению  с  другими  математическими  конструкциями  сплайны  обладают  важными  преимуществами:  лучшими  аппроксимативными  свойствами,  что  при  равных  информационных  затратах  дает  большую  или  равную  точность  при  менее  информативных  исходных  данных;  простотой  реализации  полученных  на  их  основе  алгоритмов  на  ЭВМ;  универсальностью,  позволяющей  использовать  одни  и  те  же  аппроксимирующие  конструкции  для  различных  математических  объектов.

Сплайн-функция  —  это  определенная  в  области    кусочно-полиномиальная  функция,  т.  е.  функция,  для  которой  существует  разбиение    на  подобласти  такое,  что  внутри  каждого  элемента  разбиения  функция  представляет  собой  многочлен  некоторой  степени  . 

Кубические  сплайны.  Пусть  на    задана  непрерывная  функция    и  сетка  узлов  ,  тогда  ,  .

Интерполяционным  кубическим  сплайном,  соответствующим  данной  функции    и  данной  сетке  узлов  ,  называется  функция  ,  удовлетворяющая  следующим  условиям:  на  каждом  сегменте    функция    является  многочленом  третьей  степени;  функция    является  многочленом  третьей  степени;  функция  ,  а  также  ее  первая  и  вторая  производные  непрерывны  на  ;  .

Сплайн    на  каждом  из  отрезков    определяется  четырьмя  коэффициентами,  а  на  всем  отрезке    –    коэффициентами.  Условие  его  непрерывности  и  непрерывности  его  первой  и  второй  производных  в  узлах  ,    сетки  дает    уравнения  для  неизвестных  коэффициентов.

Два  дополнительных  соотношения  задают  в  виде  граничных  условий,  наиболее  употребительными  из  которых  являются:

Построение  сплайна.  На  каждом  из  отрезков    кубический  сплайн  имеет  вид:

где:  —  неизвестные  коэффициенты,  подлежащие  определению.

Первая,  вторая,  третья  производные    имеют  вид:

Отсюда  при 

Условие  интерполирования  дает

Выражение  (5)  доопределяется  условием  при  .  Требование  непрерывности  функции    приводит  к  условиям

Отсюда  с  учетом  (1)  получается

Обозначим    —  шаг  интерполяции,  и  полученное  выражение  переписывается  в  виде:

Требование  непрерывности  первой  производной  сплайна  дает  уравнение

Из  условия  непрерывности  второй  производной    получается

Уравнения  (6)—(9)  составляют  систему    уравнений  относительно  коэффициентов  .  Два  недостающих  уравнения  задают  граничными  условиями  для    или  производных 

Интеграл  эрмитова  сплайна  на  отрезке  интерполяции  для  непрерывной  конечной  функции  имеет  вид:

  (10)

Эрмитов  сплайн  на  участке  между  узлами  интерполяции    представляет  собой  кубическую  параболу.  Коэффициенты  ,    определяются  по  формулам    и    ,  где  .

Звено  эрмитова  сплайна  имеет  вид:

.

Интегрируя  это  выражение,  получается:

Полный  интеграл    интерполянта  на  отрезке    получается  путем  суммирования  (11):

выражение  (12)  принимает  вид

Подставляя  в  (13)  значения    и    ,  получается:

Таким  образом,  интеграл  эрмитова  сплайна  непрерывной  конечной  функции    на  отрезке    определяется  шагом  интерполяции  ,  значениями  функции    в  узлах  интерполяции  ,    и  значением  производной  функции    в  точках  ,  .

Оценка  точности  интегрирования  при  интерполяции  сплайнами.  На  рис.1  показаны  графики  характерной  функции  ,  определяющей  прохождение  луча  через  световод,  эрмитова  сплайна    для  функции    и  ошибки  интерполяции  .  Кривые  построены  для  функции

Рисунок  1.  Графики  функции  ,  определяющей  прохождение  луча  через  световод,  эрмитова  сплайна    для  функции    и  ошибки  интерполяции 

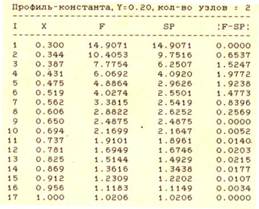
В  табл.  1  приведены  значения  ,    и    на    Ошибка  интерполяции  сплайна  оцениваются  формулой 

,  h  —  шаг  интерполяции,  которая  используется  для  вычисления  количества  секторов  интерполяции  ,  если  задана  точность  интерполяции

Таблица  1.

Результаты  расчета  погрешности  интерполяции

Естественно,  что  с  увеличением  числа    повышается  точность  интегрирования    В  табл.2  показана  зависимость  ошибки  интегрирования  функции    на    от  количества  узлов   

Таблица  2.

Результаты  расчета  зависимости  погрешности  интегрирования  от  количества  узлов

Ошибка    равна

где    вычисляется  по  формуле  (14),  а  интеграл 

Если  один  из  пределов  интегрирования  является  особой  точкой,  то  построения  сплайна  одновременно  на  всем  интервале  затруднительно.  В  случае,  когда    быстро  изменяется,  вычисление    по  формуле  (16)  не  рационально.  Порядок  четвертой  производной  функции,  определяемый  показателем  преломления  световода,  изменяется  от  двух  до  50  и  более.  Очевидно,  что  разбиение  интервала  на  подинтервалы,  внутри  которых  шаг  интерполяции  постоянен,  следует  выполнять  в  зависимости  от  характера  поведения  .

Исследование  зависимости  точности  интеграла  типа  (15)  с  особой  точкой  в  одном  из  пределов  интегрирования  от  коэффициента  деления  на  подинтервалы    показало,  что  особая  точка  .  Интеграл  интегрирования  ]  разбивался  на  подинтервалы  где  , 

Таким  образом,  с  увеличением    (при  ),  а  значит  и    уменьшается  подинтервал  примерно  в    раз.  Количество  зон  интерполяции    на  каждом  из  подинтервалов    определяется  по  (16).  Если  интеграл  сплайна  на  очередном  подинтервале  отвечает  условию

где:    —  точность  интегрирования,  то  определяются  границы  следующего  подинтервала  и  процесс  продолжается.  Вычисления  прекращаются  при

При  вычислении    используются  формулы  производных  (15)—(17),  а  также

И

Поскольку  в  модельной  функции  ,  то

Результаты  модельных  исследований  зависимости  точности  интегрирования  от  ,  ,    приведены  в  таблицах  3  и  4,  из  которых  видно,  что  для  получения  точности  0,0001  оптимальными  параметрами  являются

Описанная  методика  может  быть  использована  при  решении  прямой  задачи  рефракции  световода  с  произвольным  профилем  его  показателя  преломления,  например,  с  обобщенно-параболическим

Таблица  3.

Результаты  модельных  исследований  зависимости  точности  интегрирования  от  ,  , 

Таблица  4.

Результаты  модельных  исследований  зависимости  точности  интегрирования  от  ,  , 

Параметры  ,    аналогичны  (20).  Полученные  значения  угла  рефракции  для  точек  входа    и    полностью  совпадают  с  теми  значениями  угла  рефракции,  которые  получены  с  использованием  метода  Симпсона.  Однако  время  счета  увеличивается  примерно  в  1,5  раза.

Список  литературы:

1. Андросик  А.Б.,  Воробьев  С.А.,  Мировицкая  С.Д.  Рефракционный  метод  исследования  волоконных  световодов.  Lambert  Acamic  Publisting  2012  —  183  с.
2. Лазарев  Л.П.,  Мировицкая  С.Д.  Контроль  геометрических  и  оптических  параметров  волокон.  М.:  Радио  и  связь,  1988.  —  280  с.