Статья опубликована в рамках: V Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 28 апреля 2013 г.)
Наука: Математика
Секция: Вещественный, комплексный и функциональный анализ
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
РАЗЛОЖЕНИЕ ДВОЙНЫХ ФУНКЦИОНАЛЬНЫХ РЯДОВ КОМПЛЕКСНОГО И ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО ПО БЕСКОНЕЧНЫМ ДИАГОНАЛЯМ
Корнеев Антон Александрович
студент 3 курса, факультет точных наук и инновационных технологий МГГУ им. Шолохова, г. Москва
E-mail: predsedatel_2012@mail.ru
Дорошкевич Ольга Александровна
канд. физ.-мат. наук, доцент МГГУ им. Шолохова, г. Москва
Разложение двойных рядов по бесконечным диагоналям [3, с. 61] справедливо и для двойного функционального ряда.
Теорема 4. Если двойной функциональный ряд

сходится равномерно по ![]() и
и![]() для всех действительных значений
для всех действительных значений ![]() (или комплексных чисел
(или комплексных чисел ![]() ), лежащих внутри интервала
), лежащих внутри интервала ![]() (или принадлежащих некоторому открытому множеству комплексных чисел
(или принадлежащих некоторому открытому множеству комплексных чисел ![]() ), где
), где ![]() (
(![]() ),то имеет место разложение данного ряда по бесконечным диагоналям
),то имеет место разложение данного ряда по бесконечным диагоналям


Доказательство. Учитывая то, что подобное разложение имеет место для числовых рядов [4]и, используя возможность предельного перехода под знаком суммы для равномерно сходящихся рядов, можно обобщить его на случай функциональных рядов действительного и комплексного переменного. Необходимость условия равномерной сходимости очевидна, ибо в противном случае был бы недопустим предельный переход к некоторому ![]() , лежащему внутри интервала
, лежащему внутри интервала ![]() (или к некоторому
(или к некоторому ![]() , принадлежащему некоторому открытому множеству комплексных чисел
, принадлежащему некоторому открытому множеству комплексных чисел ![]() ).
).
Заметим, что если ряд разделим по индексам, нам достаточна равномерная сходимость каждого ряда в отдельности [4].
![]() Вычислим сумму двойного функционального ряда действительного переменного, разложив его по бесконечным диагоналям,
Вычислим сумму двойного функционального ряда действительного переменного, разложив его по бесконечным диагоналям, ![]()

Т. к. двойной ряд разделим по индексам

И в заданных интервалах ряды сходятся равномерно, то допустимо разложение




Приведение разложения двойных функциональных комплексных рядов по бесконечным диагоналям к рядам лорановского типа
Нами доказана справедливость данного разложения

Приведем формулу разложения двойных функциональных рядов комплексного переменного по бесконечным диагоналям к другому виду
Во второй сумме

заменим ![]() на
на![]()

и![]() на
на ![]()
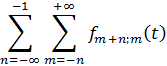
Окончательно получаем разложение в следующем виде

![]() при
при ![]() и
и ![]() при
при ![]()
Если для разложения двойных функциональных рядов комплексного переменного по бесконечным диагоналям выполняется условие:
![]() или
или
![]() , где
, где![]() ;
; ![]() ;
;![]() и
и ![]() — комплексные числа, то данное разложение есть разложение в ряд Лорана
— комплексные числа, то данное разложение есть разложение в ряд Лорана

где коэффициент ![]() определяется следующим образом
определяется следующим образом

Заметим, что если ![]() для всех
для всех ![]() и
и ![]() , то
, то

Когда в разложении данное равенство будет иметь место, то будем полагать ![]() , ибо в таких случаяхкоэффициент
, ибо в таких случаяхкоэффициент![]() однозначно определяется для
однозначно определяется для![]() и
и ![]() .
.
Если положить ![]() , то будем иметь
, то будем иметь

Далее будем рассматривать аналитически продолженные функции [2, с. 74].
![]() Рассмотрим производящую функцию
Рассмотрим производящую функцию ![]() для бесселевых функций [1, с. 14], где
для бесселевых функций [1, с. 14], где ![]() и
и ![]() — независимые комплексные переменные,
— независимые комплексные переменные,![]()

Первый ряд в произведении сходится равномерно для всех конечных![]() и
и ![]() по признаку Вейерштрасса [2, с. 21], ибо найдутся такие
по признаку Вейерштрасса [2, с. 21], ибо найдутся такие ![]() и
и![]() , при которых будет выполняться неравенство
, при которых будет выполняться неравенство

Второй ряд сходится равномерно для всех![]() и
и ![]() , за исключением
, за исключением ![]() , по признаку Вейерштрасса, ибо найдутся такие
, по признаку Вейерштрасса, ибо найдутся такие![]() и
и![]() , при которых будет выполняться неравенство
, при которых будет выполняться неравенство
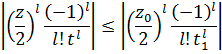
Т. к. двойной ряд сходится равномерно и условие приведения разложения к ряду лорановского типа выполнено, то получаем



для целых ![]() имеем
имеем

а для целых ![]()

![]() Найдем сумму ряда, где
Найдем сумму ряда, где ![]() — независимая комплексная переменная
— независимая комплексная переменная
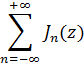
Данный ряд можно представить в форме повторных рядов

Они сходятся равномерно по признаку Вейерштрасса в силу того, что найдется такое ![]() , при котором будут выполняться неравенства
, при котором будут выполняться неравенства


В силу равномерной сходимости получаем
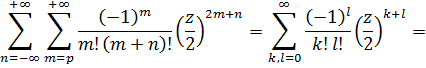

Или, используя свойство
![]()
Имеем
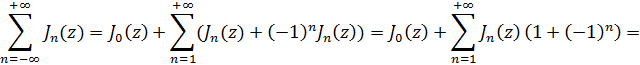



Где ряды, полученные разделением четных и нечетных индексов ![]() , очевидно, есть разложения
, очевидно, есть разложения



Хотя, мы могли бы найти эту сумму из примера 6) путем предельного перехода под знаком суммы при ![]() , что, очевидно, правомерно в силу его равномерной сходимости.
, что, очевидно, правомерно в силу его равномерной сходимости.
![]() Представим функции
Представим функции ![]() и
и ![]() в форме произведения двух рядов и разложим полученные двойные ряды по бесконечным диагоналям,
в форме произведения двух рядов и разложим полученные двойные ряды по бесконечным диагоналям, ![]() — независимые комплексные переменные,
— независимые комплексные переменные, ![]() ,
, ![]()
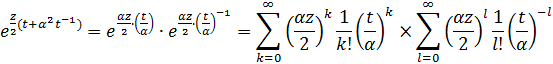
Первый ряд в произведении сходится равномерно для всех ![]() по признаку Вейерштрасса, ибо найдутся такие
по признаку Вейерштрасса, ибо найдутся такие![]() и
и![]() , при которых будет выполняться неравенство
, при которых будет выполняться неравенство

Второй ряд сходится равномерно для всех ![]() , за исключением
, за исключением ![]() , по признаку Вейерштрасса, ибо найдутся такие
, по признаку Вейерштрасса, ибо найдутся такие![]() и
и![]() , при которых будет выполняться неравенство
, при которых будет выполняться неравенство

Т. к. двойной ряд сходится равномерно и условие приведения разложения к ряду лорановского типа выполнено, то получаем


И для другой функции

Оба ряда сходятся равномерно для всех конечных ![]() по признаку Вейерштрасса, ибо найдется такое
по признаку Вейерштрасса, ибо найдется такое ![]() , при котором будет выполняться неравенство
, при котором будет выполняться неравенство
![]()
Получаем

Хотя данное разложение можно было получить, из первого, перейдя в нем к пределу под знаком суммы при ![]() и
и ![]() , что правомерно, в силу установленной выше равномерной сходимости.
, что правомерно, в силу установленной выше равномерной сходимости.
Получили разложения

Первая функция есть производящая функция для функций Инфельда [1, с. 17]. Условие приведения разложения двойного ряда по бесконечным диагоналям к ряду лорановского типа, очевидно, выполнено.
Второе разложение — есть разложение комплексной экспоненциальной функции по функциям Инфельда. Заметим, что разложение верно и для экспоненциальной функции действительной переменной.
![]() Выполним для производящей функции для функций Инфельда некоторые преобразования
Выполним для производящей функции для функций Инфельда некоторые преобразования

При ![]() и
и ![]() получаем формулу
получаем формулу

При ![]() получаем
получаем





При ![]()





Отсюда следует, что первые три слагаемые четны, а два последующие — нечетны.
Список литературы:
1.Бейтмен Г., А. Эрдейн Высшие трансцендентные функции. Функции Бесселя, функции параболического цилиндра, ортогональные многочлены. — М.: наука, 1966. —296 с.: ил. — (серия: «справочная математическая литература»).
2.Евграфов М.А. Аналитические функции: учеб.пособие. 4-е изд., стер. — СПб.: Лань, 2008. — 448 с. — (Учебники для вузов. Специальная книга).
3.Корнеев А.А. Разложение S-кратных рядов по бесконечным диагоналям для двух и трех индексов // Теория и практика современной науки: мат-лы V Междунар. науч.-практ.конф.: в 2 т. Т. 1. — М.: Спецкнига, 2012.
4.Корнеев А.А. Обобщение теории двойных рядов Прингсгейма // Тенденции развития естественных и математических наук: мат-лымеждунар. науч.-практ. конф., 2013.
дипломов


Оставить комментарий