Статья опубликована в рамках: VIII Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 22 июля 2013 г.)
Наука: Математика
Секция: Вещественный, комплексный и функциональный анализ
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
КРАЕВАЯ ЗАДАЧА ГАЗЕМАНА В ДРОБНЫХ ПРОСТРАНСТВАХ БЕСОВА
Альсейтов Амангельды Гумарович
учитель математики, гимназия «Умит», г. Уральск, Казахстан
E-mail:
HASEMAN BOUNDARU VALUE PROBLEM IN BESSOVʼS FRACTIONAL SPACES
Аlseitov Аmangeldy
teacher of mathematics, gymnasium «Umit», Uralsk city, Каzakhstan
АННОТАЦИЯ
Настоящая работа посвящена исследованию краевой задачи Газемана в дробных пространствах Бесова. Решение поставленной задачи явно выражено через интеграл типа Коши. Доказана полная непрерывность одного интегрального оператора в дробных пространствах Бесова.
ABSTRACT
This work is devoted to the research of Haseman boundary value problem in Bessovʼs fractional spaces. Solution of given task is clearly expressed through Cauchy-type integral. Is was completely proven continuity of a certain integral operator in Bessovʼs fractional spaces.
Ключевые слова: краевая задача cо сдвигом; сингулярное интегральное уравнение; интеграл типа Коши; вполне непрерывный оператор; краевая задача Газемана; дробное пространство.
Keywords: boundary value problem with shift; singular integral equation; Cauchy-type integral; completely continuous operator; Haseman boundary value problem; fractional space.
Применение дробных пространств к изучению разрешимости краевых задач началось в начале 50-х годов прошлого столетия.
В настоящей работе изучается одна краевая задача со сдвигом в дробных пространствах Бесова, а именно задача Газемана. Краевыми задачами со сдвигами называются задачи, краевые условия которых представляют собой линейные соотношения между предельными значениями искомых аналитических функций, вычисленными в различных точках границы. С такими краевыми задачами тесно связаны сингулярные уравнения, линии особенностей которых задаются гомеоморфными отображениями контура интегрирования на себя.
Впервые краевую задачу со сдвигом предложил рассматривать С. Газеман в работе [13], опубликованной в 1907 г. Поставленная им задача обобщала задачу Римана [6, с. 106] в том смысле, что предельное значение внутренней компоненты искомой кусочно-аналитической функции вычислялось в точке α(t), полученной из t сохраняющим ориентацию гомеоморфизмом простого замкнутого гладкого контура Г на себя. В 1932 г. в докладе [14], прочитанном II Международному математическому съезду, Т. Карлеман поставил носящую ныне его имя краевую задачу об отыскании аналитической внутри Г функции по условию линейного сопряжения её граничных значений в точках t и a(t), где a(t) — изменяющий ориентацию на Г гомеоморфизм, удовлетворяющий условию ![]() .
.
Дальнейшее развитие теории обеспечивалось исключительно трудами математиков бывшего СССР. Прежде всего, следует отметить основополагающие работы Д.А. Квеселава [7—10], опубликованные в 1946—1948 гг. Используя метод интегральных уравнений, Д.А. Квеселава дал для случая односвязной области полное решение задач Газемана и Карлемана для ограниченной односвязной области и ещё двух аналогичных задач.
К настоящему времени исследование основных краевых задач со сдвигом в классической постановке приняло почти законченный вид. Но до сих пор остается открытым вопрос, поставленный Ф.Д. Гаховым: с какого максимально широкого класса можно взять коэффициенты задачи, чтобы решение задачи Римана оставалось в классе непрерывных функций [6, с. 146].
Эллиптические системы дифференциальных уравнений первого порядка на плоскости и краевые задачи, а также основы общей теории обобщенных аналитических функций в дробных пространствах Никольского-Бесова изучены Н.К. Блиевым, и основные результаты исследований изложены в монографиях [5], [12]. Полученные Н.К. Блиевым результаты вполне применимы к изучению в дробных пространствах Бесова многих краевых задач теории функций. Некоторые результаты в этом направлении получены И.А. Абитбековым [1], [2]. Изучение дифференциальных уравнений и краевых задач к ним в дробных пространствах без предположения достаточной гладкости коэффициентов начато, по-видимому, в работах Н.К. Блиева.
Рассмотрим следующий интегральный оператор:
, (1)
где: Г — простой замкнутый контур класса Ляпунова , , ограничивающий конечную область точек
комплексной плоскости, а a(t) обозначает некоторую непрерывную функцию, заданную на Г и переводящую взаимно однозначно контур Г в самого себя с сохранением направления. Будем считать, что функция сдвига a(t) имеет производную
отличную от нуля всюду на Г и принадлежащую классу Бесова
![]() .
.
Известно, что если a'(t) из класса Гельдера, то оператор K вполне непрерывен [6], [11]. Это тем более верно, когда a'(t) из класса бесконечно дифференцируемых в Г функций. Ниже рассмотрим оператор K в пространствах
![]() .
.
Рассмотрим ядро оператора (1)
 (2)
(2)
и оценим её.
Совершив над ядром ![]() преобразование и учитывая очевидные равенства
преобразование и учитывая очевидные равенства
 ,
,
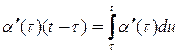 ,
,
Получим
 . (3)
. (3)
По условию задачи существует производная  . Как известно,
. Как известно, ![]() [3], т.е. функция
[3], т.е. функция ![]() является непрерывной на
является непрерывной на ![]() . Применяя формулу Лагранжа о конечных приращениях, имеем
. Применяя формулу Лагранжа о конечных приращениях, имеем
![]() (4)
(4)
где: ![]() и
и ![]() на контуре
на контуре ![]() . Заметим, что
. Заметим, что ![]() . Действительно, по условию
. Действительно, по условию ![]() непрерывная и нигде
непрерывная и нигде ![]() на
на ![]() , поэтому можно подобрать такое число
, поэтому можно подобрать такое число ![]() , что
, что ![]() . Отсюда в свою очередь следует, что
. Отсюда в свою очередь следует, что ![]() .
.
Оценим числитель правой части (3)

где: ![]() — независимая постоянная.
— независимая постоянная.
Далее, обозначив, ![]() будем иметь
будем иметь

 (5)
(5)
Для получения второго неравенства в (5) использовалось неравенство Гельдера. Отметим, что оценку (5) можно было бы получить, рассматривая, так называемую стандартную дугу контура ![]() [11, с. 16].
[11, с. 16].
Объединив (4) и (5) получим оценку ядра

 (6)
(6)
где: ![]() , а
, а ![]() как и выше минимум функции
как и выше минимум функции ![]() на контуре
на контуре ![]() .
.
Теперь нетрудно показать ограниченность оператора
 , (1)
, (1)
точнее, верна следующая лемма.
Лемма 1. В пространстве  справедлива следующая оценка нормы оператора
справедлива следующая оценка нормы оператора ![]() :
:
![]() , (7)
, (7)
где: ![]() ‒ независимая постоянная.
‒ независимая постоянная.
Доказательство. Используя оценку (6) имеем

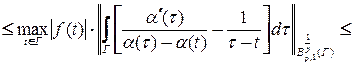
 ,
,
где: ![]() — полунорма в пространстве
— полунорма в пространстве  [5, с. 16]. Отсюда следует справедливость оценки (7).
[5, с. 16]. Отсюда следует справедливость оценки (7).
Теперь перейдем к доказательству основной леммы.
Лемма 2 (основная лемма). Пусть  . Тогда оператор
. Тогда оператор ![]() вполне непрерывен в пространствах
вполне непрерывен в пространствах  .
.
Доказательство. Множество бесконечно дифференцируемых на контуре ![]() функций
функций ![]() плотно в пространствах
плотно в пространствах  [4]. В силу этого существует такая последовательность функций
[4]. В силу этого существует такая последовательность функций ![]() из пространства
из пространства ![]() , что
, что
 . (8)
. (8)
Очевидно, что при каждом ![]() оператор
оператор
 (9)
(9)
есть вполне непрерывный оператор, переводящий  в себя.
в себя.
Поступая так же, как и выше приведем ядро
 (10)
(10)
оператора ![]() к виду (3)
к виду (3)
 (11)
(11)
и рассмотрим разность ядер (2) и (10)
![]()

 =
=
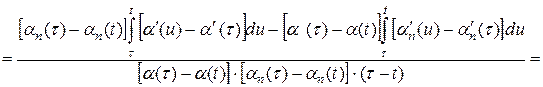
![]()



 +
+
 . (12)
. (12)
В силу того, что ![]() и
и ![]() ,
, ![]() 1, 2, … , непрерывно дифференцируемые функции, применяя теорему о конечных приращениях, имеем оценку
1, 2, … , непрерывно дифференцируемые функции, применяя теорему о конечных приращениях, имеем оценку

![]() , (13)
, (13)
где: ![]() ,
, ![]() — положительная постоянная. В силу
— положительная постоянная. В силу ![]() на
на ![]() и
и ![]() при
при ![]() можем считать, что, начиная с некоторого номера все
можем считать, что, начиная с некоторого номера все ![]() .
.
Выше (лемма 1) было доказано нами, что оператор ![]() ограничен в
ограничен в ![]() . В силу этого и формул (7)—(13) будем иметь
. В силу этого и формул (7)—(13) будем иметь

![]()
 +
+
+
![]()


![]()
![]() ,
,
где: ![]() и как отмечено выше все
и как отмечено выше все ![]() на
на ![]() .
.
Откуда в силу (8) следует, что
![]() при
при ![]() .
.
Следовательно, оператор ![]() вполне непрерывен в пространстве
вполне непрерывен в пространстве  ,
, ![]() как равномерный предел вполне непрерывных операторов
как равномерный предел вполне непрерывных операторов ![]() по норме этого пространства. Основная лемма доказана.
по норме этого пространства. Основная лемма доказана.
Перейдем теперь к основному вопросу нашей работы, к следующей задаче линейного сопряжения со сдвигом, называемой также краевой задачей Газемана.
Дан замкнутый простой контур класса Ляпунова ![]() ,
, ![]() , делящий комплексную плоскость на две части: внутреннюю область
, делящий комплексную плоскость на две части: внутреннюю область ![]() , содержащую начало координат и внешнюю область
, содержащую начало координат и внешнюю область ![]() , содержащую бесконечно удаленную точку. Положительным направлением на контуре
, содержащую бесконечно удаленную точку. Положительным направлением на контуре ![]() будем считать то направление, которое область
будем считать то направление, которое область ![]() оставляет слева. На контуре
оставляет слева. На контуре ![]() заданы функции
заданы функции ![]() и
и ![]() из класса Бесова
из класса Бесова  ,
, ![]() , причем,
, причем, ![]() не обращается в нуль нигде на
не обращается в нуль нигде на ![]() . Считаем, что
. Считаем, что ![]() удовлетворяет условию
удовлетворяет условию  . Пусть функция
. Пусть функция ![]() , заданная на контуре
, заданная на контуре ![]() и имеющая отличную от нуля производную
и имеющая отличную от нуля производную  ,
, ![]() , взаимно однозначно отображает контур
, взаимно однозначно отображает контур ![]() на себя с сохранением направления.
на себя с сохранением направления. ![]() будем называть функцией сдвига. Через
будем называть функцией сдвига. Через ![]() обозначим функцию, обратную
обозначим функцию, обратную ![]() . Легко убедиться, что свойства
. Легко убедиться, что свойства ![]() такие же, как и у функции
такие же, как и у функции ![]() .
.
Постановка задачи:
Найти кусочно-аналитическую функцию ![]() , имеющую конечный порядок на бесконечности, удовлетворяющую на
, имеющую конечный порядок на бесконечности, удовлетворяющую на ![]() краевому условию
краевому условию
![]() . (14)
. (14)
![]() и
и ![]() обозначают пределы
обозначают пределы ![]() , когда
, когда ![]() стремится к точке
стремится к точке ![]() , соответственно, из
, соответственно, из ![]() и
и ![]() .
.
Эта задача представляет естественное обобщение краевой задачи Римана в дробных пространствах Бесова, рассмотренной И.А. Абитбековым [1], которая соответствует случаю ![]() .
.
Законченное решение задачи в классическом случае впервые было дано Д.А. Квеселава [7]. Позже Ф.Д. Гахов решил ее несколько иным путем, комбинируя для решения задачи метод интегральных уравнений с методом конформного склеивания [6]. Мы будем следовать методу интегральных уравнений, предложенному Д.А. Квеселава [7].
В настоящей работе рассмотрим задачу Газемана с коэффициентом ![]() и свободным членом
и свободным членом ![]() , принадлежащими классу непрерывных функций из пространства Бесова
, принадлежащими классу непрерывных функций из пространства Бесова  Ì®
Ì®![]() ,
, ![]() , но
, но 
![]() ®
®![]() при любом
при любом ![]() , т.е. в нашем случае
, т.е. в нашем случае ![]() и
и ![]() являются непрерывными на
являются непрерывными на ![]() , но не являются непрерывными по Гельдеру. Производная функции сдвига
, но не являются непрерывными по Гельдеру. Производная функции сдвига  ,
, ![]() . Как увидим ниже, краевые значения
. Как увидим ниже, краевые значения ![]() и
и ![]() искомой кусочно-аналитической функций являются непрерывными (не гельдеровыми) функциями на
искомой кусочно-аналитической функций являются непрерывными (не гельдеровыми) функциями на ![]() .
.
Имеет место следующая лемма [7].
Лемма 3. Если кусочно-аналитическая функция ![]() , ограниченная на бесконечности, удовлетворяет на
, ограниченная на бесконечности, удовлетворяет на ![]() краевому условию
краевому условию
![]() ,
,
то ![]() тождественно равна постоянному.
тождественно равна постоянному.
Если ![]() , то решением задачи, как легко видеть, будет функция тождественно равная нулю.
, то решением задачи, как легко видеть, будет функция тождественно равная нулю.
Пусть ![]() . В этом случае краевое условие (14) примет вид
. В этом случае краевое условие (14) примет вид
![]() . (15)
. (15)
Будем искать решение этой задачи в виде

 (16)
(16)
где ![]() – искомая функция точек контура
– искомая функция точек контура ![]() , принадлежащая
, принадлежащая  ,
, ![]() ,
, ![]() — произвольный полином.
— произвольный полином.
В силу леммы [5, с. 59], ![]()
 ,
, ![]() . Любой полином
. Любой полином ![]() есть функция класса
есть функция класса  ,
, ![]() ,
, ![]() . Отсюда и из леммы [5, с. 61], следует, что
. Отсюда и из леммы [5, с. 61], следует, что ![]()
 Ì®
Ì®![]() , а краевые значения
, а краевые значения ![]() и
и ![]() принадлежат пространству
принадлежат пространству  Ì®
Ì®![]() ,
, ![]() .
.
Из формул (16), пользуясь формулами Сохоцкого, справедливость которых в классах Бесова доказана Н.К. Блиевым [5, с. 64], получим


Подставляя эти выражения в краевое условие (15), имеем:
 . (17)
. (17)
По основной лемме это интегральное уравнение Фредгольма. На основании леммы 3 однородное уравнение ![]() не имеет (нетривиального) решения. Следовательно, неоднородное уравнение (17) разрешимо для любой правой части. Любой полином
не имеет (нетривиального) решения. Следовательно, неоднородное уравнение (17) разрешимо для любой правой части. Любой полином ![]() есть функция класса
есть функция класса  ,
, ![]() . Нетрудно доказать, что для
. Нетрудно доказать, что для ![]()
 и
и  ,
, ![]() , решение уравнения (17) также будет из этого класса. Согласно следствия 1.4.2 [5, с. 62], особый интеграл с ядром Коши переводит функции класса
, решение уравнения (17) также будет из этого класса. Согласно следствия 1.4.2 [5, с. 62], особый интеграл с ядром Коши переводит функции класса  ,
, ![]() в себя. Это тем более справедливо для интеграла с более слабой особенностью. Любому решению уравнения (17) формула (16) приводит в соответствие кусочно-аналитическую функцию
в себя. Это тем более справедливо для интеграла с более слабой особенностью. Любому решению уравнения (17) формула (16) приводит в соответствие кусочно-аналитическую функцию ![]() , являющуюся некоторым решением задачи сопряжения (15).
, являющуюся некоторым решением задачи сопряжения (15).
Пользуясь леммой 3, получим:
Теорема 1. Любое кусочно-аналитическое решение задачи сопряжения (16), имеющее конечный порядок на бесконечности, дается формулами (16), где ![]() — произвольный полином, а
— произвольный полином, а ![]() — решение интегрального уравнения (17).
— решение интегрального уравнения (17).
Легко заметить, что задача сопряжения (15) имеет единственное решение, исчезающее на бесконечности. Это решение дается формулой (16), где нужно положить ![]() , а под
, а под ![]() подразумевается решение уравнения (17) при
подразумевается решение уравнения (17) при ![]() .
.
Рассмотрим теперь задачу сопряжения с однородным краевым условием
![]() . (18)
. (18)
Число ![]() , определяемое формулой
, определяемое формулой
![]() ,
,
где символ [ ]Г обозначает приращение выражения, заключенного в скобки, при обходе контура ![]() один раз в положительном направлении, назовем как обычно, индексом заданной на
один раз в положительном направлении, назовем как обычно, индексом заданной на ![]() функции
функции ![]() , или индексом задачи сопряжения.
, или индексом задачи сопряжения.
Предполагая, что точка ![]() расположена в области D+, рассмотрим функцию
расположена в области D+, рассмотрим функцию
G0(t)= t-χ × G(t),
где χ индекс функции ![]() . Очевидно, что индекс функции
. Очевидно, что индекс функции ![]() равен нулю, поэтому под
равен нулю, поэтому под ![]() на контуре
на контуре ![]() будем понимать одну определенную произвольно выбранную ветвь, непрерывно меняющуюся на
будем понимать одну определенную произвольно выбранную ветвь, непрерывно меняющуюся на ![]() . Функция
. Функция ![]() принадлежит классу
принадлежит классу  ,
, ![]() [1].
[1].
Функция, определяемая формулами
![]()
![]() (19)
(19)
 (20)
(20)
где: ![]() — решение уравнения
— решение уравнения ![]() , является некоторым (частным) решением однородной задачи сопряжения (18). Действительно, из формул (20), пользуясь формулами Сохоцкого, получим
, является некоторым (частным) решением однородной задачи сопряжения (18). Действительно, из формул (20), пользуясь формулами Сохоцкого, получим


Подставляя эти выражения в (19), имеем
 (21)
(21)

Рассмотрим, далее, задачу сопряжения
![]() (22)
(22)
Запишем ее в виде
![]() (23)
(23)
Функция ![]() имеет нулевой индекс. Логарифмируя (23), получим
имеет нулевой индекс. Логарифмируя (23), получим
![]()
Учитывая (21), будем иметь
 (24)
(24)
Определив отсюда ![]() , затем по формулам (19) и (20) найдем
, затем по формулам (19) и (20) найдем ![]() . Из самого хода рассуждения видно, что найденная функция
. Из самого хода рассуждения видно, что найденная функция ![]() является решением задачи сопряжения (22). Эта функция
является решением задачи сопряжения (22). Эта функция ![]() , называемая каноническим решением однородной задачи (18), как видно из (19), нигде на конечном расстоянии в нуль не обращается. Порядок канонического решения на бесконечности равен (-χ).
, называемая каноническим решением однородной задачи (18), как видно из (19), нигде на конечном расстоянии в нуль не обращается. Порядок канонического решения на бесконечности равен (-χ).
Переписав краевое условие (18) в виде

и используя теорему 1, получим:
Теорема 2. Любое кусочно-аналитическое решение однородной задачи сопряжения (18), имеющее конечный порядок на бесконечности, дается формулами


где: ![]() — произвольный полином,
— произвольный полином,
![]() — каноническое решение задачи (18) и
— каноническое решение задачи (18) и
![]() — решение интегрального уравнения
— решение интегрального уравнения ![]() .
.
Если χ£0, то однородная задача сопряжения (18) не имеет (нетривиального) решения, исчезающего на бесконечности; если χ > 0, то она имеет ровно χ линейно независимых решений, исчезающих на бесконечности.
Перейдем теперь к неоднородной задаче (14). Пусть ![]() — каноническое решение однородной задачи, получаемой из (14) при
— каноническое решение однородной задачи, получаемой из (14) при ![]() . Тогда краевое условие (14) можно записать в виде
. Тогда краевое условие (14) можно записать в виде

и на основании теоремы 1 получается
Теорема 3. Любое кусочно-аналитическое решение неоднородной задачи сопряжения (14), имеющее конечный порядок на бесконечности, дается формулами

где: ![]() — произвольный полином,
— произвольный полином,
![]() — каноническое решение соответствующей однородной задачи и
— каноническое решение соответствующей однородной задачи и
![]() — решение интегрального уравнения
— решение интегрального уравнения 
Список литературы:
1.Абитбеков И.А. О задаче линейного сопряжения для многосвязной области в дробных пространствах // Функциональный анализ, дифференциальные уравнения и их приложения // Сб. научн. тр. — Алматы, — 1982. — С. 3—9.
2.Абитбеков И.А., Блиев Н.К. О разрешимости обобщенной задачи Римана-Гильберта для многосвязной области в дробных пространствах // Изв. АН Каз ССР. — Сер. физ. -мат. — 1983. № 1. — С. 1—4.
3.Бесов О.В. Об условиях существования классического решения волнового уравнения // Сиб. матем. журн. — 1967. — Т. 8. № 2. — С. 243—256.
4.Бесов О.В., Ильин В.П., Никольский С.М. Интегральные представления функций и теоремы вложения. М.: Наука, 1975. — 480 с.
5.Блиев Н.К. Обобщенные аналитические функции в дробных пространствах. Алма-Ата: Наука, 1985. — 160 с.
6.Гахов Ф.Д. Краевые задачи. — М.: Наука, 1977. — 640 с.
7.Квеселава Д.А. Решение одной граничной задачи теории функций // Докл. АН СССР. — 1946. — Т. 53. — № 8. — С. 683—686.
8.Квеселава Д.А. Об одной граничной задачи теории функций // Сообщ. АН. Груз. ССР. — 1946. — Т. 7. — № 9—10. — С. 609—614.
9.Квеселава Д.А. Решение одной граничной задачи теории функций Т. Карлемана // Докл. АН СССР. —– 1947. — Т. 55. — № 8. — С. 683—686.
10.Квеселава Д.А. Некоторые граничные задачи теории функций // Труды Матем. ин-та. Груз. ССР. — 1948. — Т. 16. — С. 39—80.
11.Мусхелишвили Н.И. Сингулярные интегральные уравнения. М.: Физматгиз, 1968. — 512 с.
12.Bliev N. Generalized analytic functions in fractional Spaces. — Addison Wesley Longman inc., 1997.
13.Haseman C. Anwendung der Theorie der Integralgleichungen auf einige Randwertaufgaben. — Göttingen, 1907. — 192 p.
14.Karleman T. Sur la théorie des equations intégrales et ses applications // Verhandl. des Internat. Mathem. Kongr. I. — Zürich, — 1932. — P. 138—151.
дипломов


Оставить комментарий