Статья опубликована в рамках: XI Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 14 октября 2013 г.)
Наука: Математика
Секция: Дифференциальные уравнения, динамические системы и оптимальное управление
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ОБ ОДНОЙ МНОГОТОЧЕЧНОЙ КРАЕВОЙ ЗАДАЧЕ ВЫСОКОГО ПОРЯДКА
Митрохин Сергей Иванович
канд. физ.-мат. наук, доцент, старший научный сотрудник НИВЦ МГУ им. М.В. Ломоносова, г. Москва
ABOUT ONE MULTIPOINT BOUNDARY VALUE PROBLEM OF HIGH-ORDER
Sergey Mitrohin
candidate of Physical and Mathematical Sciences, associate professor, senior research scientist of Research Computing Center of M.V. Lomonosov Moscow State University, Moscow
АННОТАЦИЯ
В работе изучена краевая задача для дифференциального оператора нечётного порядка с суммируемым потенциалом с нерегулярными граничными условиями. Получено уравнение на собственные значения, изучена индикаторная диаграмма, выведена асимптотика собственных значений изучаемой краевой задачи.
ABSTRACT
The article studies a boundary value problem for a differential operator of odd order with summable potential with irregular boundary conditions. An equation on eigenvalues was established; an indicator diagram was studied; asymptotics of eigenvalues of the boundary value problem in question was found.
Ключевые слова: Дифференциальный оператор, краевая задача, индикаторная диаграмма, собственные значения, асимптотика решений.
Keywords: differential operator; boundary value problem; indicator diagram; eigenvalues; asymptotics of solutions.
Изучим следующую краевую задачу для дифференциального оператора седьмого порядка:
![]() (1)
(1)
с многоточечными граничными условиями
![]() (2)
(2)
в предположении, что потенциал ![]() является суммируемой функцией на отрезке
является суммируемой функцией на отрезке ![]() :
:  почти всюду на отрезке
почти всюду на отрезке ![]() . (3)
. (3)
Пусть ![]() , причём зафиксируем ту ветвь арифметического корня, дл я которой
, причём зафиксируем ту ветвь арифметического корня, дл я которой ![]() . Пусть
. Пусть ![]() , т.е.
, т.е. ![]() — различные корни седьмой степени из единицы:
— различные корни седьмой степени из единицы:
 (4)
(4)
Впервые дифференциальные операторы (второго порядка) с суммируемым потенциалом изучались в работах [1], [2].
Методами работ [3—5] доказывается следующее утверждение.
Теорема 1. Общее решение дифференциального уравнения (1) имеет следующий вид:
![]() (5)
(5)
где: ![]() — произвольные постоянные, причём при
— произвольные постоянные, причём при ![]() справедливы следующие асимптотические формулы:
справедливы следующие асимптотические формулы:
 (6)
(6)
 (7)
(7)
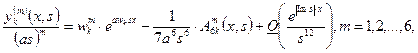 (8)
(8)
 (9)
(9)
Из формул (7)—(9) видно, что
![]() (10)
(10)
Из формул (5) – (10), используя граничные условия (2), получаем:
![]() (11)
(11)
Система (11) — однородная система из семи линейных уравнений с семью неизвестными ![]() . Из метода Крамера следует, что такая система имеет ненулевое решение
. Из метода Крамера следует, что такая система имеет ненулевое решение ![]() только в том случае, когда её определитель равен нулю. Поэтому справедлива следующая теорема.
только в том случае, когда её определитель равен нулю. Поэтому справедлива следующая теорема.
Теорема 2. Уравнение на собственные значения краевой задачи (1)—(2) с условием суммируемости потенциала (3) имеет следующий вид:
 (12)
(12)
причём асимптотики функций ![]() определены формулами (6)—(10).
определены формулами (6)—(10).
Подставляя формулы (6)—(7) в уравнение (12), разлагаем определитель ![]() на сумму определителей по столбцам, находим:
на сумму определителей по столбцам, находим:
![]() (13)
(13)
где
 (14)
(14)
![]() , где
, где ![]() получается из определителя
получается из определителя ![]() из (14) заменой
из (14) заменой ![]() -го столбца на столбец
-го столбца на столбец 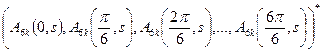 , при этом в (14) введено обозначение
, при этом в (14) введено обозначение
![]() . (15)
. (15)
Основное приближение уравнения (13)—(15) имеет вид ![]() . (16)
. (16)
По правилам вычисления определителей имеем:
![]() (17)
(17)
при этом коэффициент ![]() , т. к. перестановка чисел
, т. к. перестановка чисел ![]() четная, коэффициент
четная, коэффициент ![]() в силу того, что перестановка чисел
в силу того, что перестановка чисел ![]() нечётная.
нечётная.
В общем виде уравнение (14)—(17) можно выписать в следующем виде:
![]() (18)
(18)
где: ![]() ,
, ![]() — знак перестановки чисел
— знак перестановки чисел ![]() , при этом
, при этом ![]() при
при ![]() .
.
Из общей теории нахождения асимптотики корней уравнений вида (12)—(13) (см. [6, глава 12]) следует, что необходимо изучить индикаторную диаграмму уравнения (14) (или, что то же самое, уравнения (18)).
Для изучения индикаторной диаграммы необходимо ответить на два вспомогательных вопроса: 1) когда достигается ![]() и 2) когда достигается
и 2) когда достигается ![]() ? Имеем:
? Имеем:
 (19)
(19)
при этом в силу формулы (4) получаем:
 (20)
(20)
 (21)
(21)
причём ![]()
Из формул (19)—(21) нетрудно сообразить, что ![]() достигается, если
достигается, если ![]() (всего 8 комбинаций) и равен он
(всего 8 комбинаций) и равен он ![]()
![]() , а
, а ![]() будет в случае
будет в случае ![]()
![]() и равен он
и равен он ![]() (всего одна точка). Изучая эти восемь комбинаций, получаем вертикальный отрезок индикаторной диаграммы уравнения (18): точки
(всего одна точка). Изучая эти восемь комбинаций, получаем вертикальный отрезок индикаторной диаграммы уравнения (18): точки ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , где
, где ![]()
![]()
![]() , при этом эти точки соответствуют таким перестановкам чисел
, при этом эти точки соответствуют таким перестановкам чисел ![]() :
: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Понятно, что вторые координаты этих точек вычисляются в точном виде:
![]() ;
;![]() , и т. д.
, и т. д.
Точка ![]() , которой соответствует
, которой соответствует ![]() , имеет координаты
, имеет координаты ![]() , получается при перестановке
, получается при перестановке ![]() .
.
Изучая более подробно индикаторную диаграмму, выясняем, что она представляет собой 14-ти-угольник (правильный!!!) ![]() ,
, ![]() совпадает с точкой
совпадает с точкой ![]() ,
, ![]() совпадает с точкой
совпадает с точкой ![]() ,
, ![]() совпадает с точкой
совпадает с точкой ![]() , причём все эти точки расположены на окружности с центром
, причём все эти точки расположены на окружности с центром ![]() и радиусом
и радиусом ![]() .
.
Из общей теории (см. [6, глава 12]) следует, что корни уравнения на собственные значения (т. е. корни уравнения (13)—(15)) находятся в 14-ти секторах бесконечно малого раствора, биссектрисы которых являются серединными перпендикулярами к сторонам индикаторной диаграммы.
Изучим асимптотику собственных значений в секторе ![]() , который соответствует вертикальному отрезку индикаторной диаграммы. Из общей теории следует, что справедлива следующая теорема.
, который соответствует вертикальному отрезку индикаторной диаграммы. Из общей теории следует, что справедлива следующая теорема.
Теорема 3. Уравнение на собственные значения в секторе ![]() записывается в следующем виде:
записывается в следующем виде:
 (22)
(22)
Если элементы определителя ![]() из (12) обозначить
из (12) обозначить ![]() , где
, где ![]() , то с помощью формулы (14) обнаруживается следующее соответствие:
, то с помощью формулы (14) обнаруживается следующее соответствие: ![]() . Поэтому уравнение (22) можно переписать в следующем виде:
. Поэтому уравнение (22) можно переписать в следующем виде:
![]() (23)
(23)
Перегруппировывая слагаемые, уравнение (23) можно записать в следующем, более удобном виде:
 (24)
(24)
Таким образом, уравнение (22) на собственные значения в секторе ![]() имеет следующие решения:
имеет следующие решения:
 (25)
(25)
Например, первые из уравнений в (25) можно выписать более подробно:
 (26)
(26)
Более подробно уравнение (26) в силу формул (6) – (7) выглядит так:
 (27)
(27)
Изучая уравнение (27) методами работ [3] - [5], доказываем утверждение.
Теорема 4. Асимптотика собственных значений краевой задачи (1)—(2)—(3) в секторе ![]() (серия 1) имеет следующий вид:
(серия 1) имеет следующий вид:
![]() (28)
(28)
причём
 (29)
(29)
Формулы, аналогичные формулам (28) и (29), справедливы и для остальных секторов и серий.
В работе [7] изучалась аналогичная задача для оператора четвёртого порядка с гладким потенциалом.
Список литературы:
1.Винокуров В.А., Садовничий В.А. Асимптотика любого порядка собственных значений и собственных функций краевой задачи Штурма-Лиувилля на отрезке с суммируемым потенциалом // Дифференциальные уравнения. — 1998. — Т. 34, — № 10. — С. 1423—1426.
2.Винокуров В.А., Садовничий В.А. Асимптотика любого порядка собственных значений и собственных функций краевой задачи Штурма-Лиувилля на отрезке с суммируемым потенциалом // Известия РАН. Серия: матем. — 2000. — Т. 64, — № 4. — С. 47—108.
3.Митрохин С.И. Асимптотика собственных значений дифференциального оператора четвёртого порядка с суммируемыми коэффициентами. Вестник Московского университета. Сер.1, математика, механика. — 2009. — № 3. — С. 14—17.
4.Митрохин С.И. Спектральные свойства краевых задач для функционально-дифференциальных уравнений с интегрируемыми коэффициентами. Дифференциальные уравнения, — 2010. — Т. 46, — № 8. — С. 1085—1093.
5.Митрохин С.И. О спектральных свойствах дифференциальных операторов нечётного порядка с суммируемым потенциалом // Дифференциальные уравнения, — 2011. — Т. 47, — № 12. — С. 1808—1811.
6.Беллман Р., Кук К.Л. Дифференциально-разностные уравнения. М.: Мир, 1967. — 548 с.
7.Белабасси Ю. Регуляризованный след многоточечной задачи // Вестник Московского университета. Серия: математика. — 1981. — № 2. — С. 35—41.
дипломов


Оставить комментарий