Статья опубликована в рамках: XV Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 05 февраля 2014 г.)
Наука: Информационные технологии
Секция: Математическое моделирование, численные методы и комплексы программ
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ПРИМЕНЕНИЕ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ ПРИ РЕШЕНИЕ ПОЛУКОЭРЦИТИВНОЙ ЗАДАЧИ НЕЙМАНА
Хабибулина Татьяна Васильевна
студент ПГУ имени Ш.-Алейхема, РФ, г. Биробиджан
Е-mail: habik_tania@mail.ru
Бабинер Елена Станиславовна
старший преподаватель ПГУ имени Ш.-Алейхема, РФ, г. Биробиджан
Е-mail: mineeva_elena18@mail.ru
APPLICATION OF A FINITE ELEMENT METHOD AT THE SOLUTION OF THE SEMI-COERCIVE TASK NEUMANN
Habibulina Tatiana
student of Sholom-Aleykhema Priamursky state university Russia, Birobidgan
Babiner Еlena
senior teacher of Sholom-Aleykhema Priamursky state university Russia, Birobidgan
АННОТАЦИЯ
В статье рассмотрены краевые полукоэрцитивные задачи Неймана для одномерного и двумерного случаев и переход к их вариационным постановкам. Описываются алгоритмы аппроксимации рассматриваемых задач методом конечных элементов, представлены результаты численных расчетов.
ABSTRACT
Semi-coercive task Neiman for one-dimensional and two-dimensional cases and transition to their variation formulation are considered in the article. Algorithms of approximation tasks by finite element method are describe there and the numerical result are presented.
Ключевые слова: вторая краевая задача; метод конечных элементов.
Keywords: second boundary value problem; finite element method.
Процесс моделирования стационарных процессов (не зависящих от времени) различной физической природы (колебания, теплопроводность, диффузия и др.) обычно приводит к уравнениям эллиптического типа, на искомое решение которых накладываются дополнительные условия, вытекающие из физической (или другой) постановки задачи. Примером такой задачи является вторая краевая задача или задача Неймана, имеющая широкий спектр физических интерпретаций. В качестве ее приложения в пространстве ![]() возьмем процесс колебания струны, а в
возьмем процесс колебания струны, а в ![]() — колебания мембраны.
— колебания мембраны.
Краевая постановка полукоэрцитивной задачи Неймана в операторном виде представлена уравнением Пуассона (1) и краевым условием (2):
![]() , на
, на ![]() (1)
(1)
![]() , (2)
, (2)
где оператор  . Это математическая модель колебания струны со свободными концами.
. Это математическая модель колебания струны со свободными концами.
Классическое решение задачи (1), (2) — это дважды непрерывно дифференцируемая функция на ![]() . Если взять в качестве области определения оператора множество таких функций, то оператор
. Если взять в качестве области определения оператора множество таких функций, то оператор ![]() не будет положительным, а это значит — задача не имеет решения [6, с. 126]. В силу своей полукоэрцитивности задача (1), (2) разрешима при условии, что
не будет положительным, а это значит — задача не имеет решения [6, с. 126]. В силу своей полукоэрцитивности задача (1), (2) разрешима при условии, что  . Единственность обеспечивается выполнением требования к решению:
. Единственность обеспечивается выполнением требования к решению:
 . (3)
. (3)
Область определения оператора задачи (1), (2), усиленная требованием (3) гарантирует его положительность, следовательно, можно осуществить переход к задаче минимизации функционала:
 ,
,
где скалярное произведение определяется по формуле:  .
.
После интегрирования по частям получаем окончательный вид функционала:
 (4)
(4)
В [1, с. 9] показана справедливость утверждения о том, что если функция ![]() минимум для функционала (4), то она является решением задачи (1), (2). Обратное также имеет место: если
минимум для функционала (4), то она является решением задачи (1), (2). Обратное также имеет место: если ![]() решение задачи (1), (2), то она сообщает минимальное значение функционалу (4).
решение задачи (1), (2), то она сообщает минимальное значение функционалу (4).
Вариационная постановка этой задачи имеет преимущество, которое заключается в том, что можно ограничиться только требованием наличия у искомой функции кусочно непрерывных первых производных. Функция, доставляющая минимум функционалу (4) является обобщенным (слабым) решением краевой задачи (1), (2) [4, с. 171].
Для численного решения задачи (1), (2) методом конечных элементов переходим от непрерывной задачи к конечномерной. Произведем разбиение ![]() на
на ![]() частей:
частей: ![]() ,
, ![]() . Приближенное решение будем искать в виде линейной комбинации:
. Приближенное решение будем искать в виде линейной комбинации:

![]() (5)
(5)
где: ![]() базисные (пробные) функции заданные на разбиениях
базисные (пробные) функции заданные на разбиениях ![]() , а коэффициенты
, а коэффициенты ![]() это значения искомой функции в узлах сетки
это значения искомой функции в узлах сетки ![]() . Вид базисных функций представлен в [1, с. 100].
. Вид базисных функций представлен в [1, с. 100].
После подстановки (5) в функционал (4), получаем:
 ,
, ![]() , (6)
, (6)
где 
Принимая во внимание необходимое и достаточное условие для существования минимума выпуклого функционала, находим вариацию (6), приравниваем ее к нулю и сводим задачу к решению системы вида:
 . (7)
. (7)
![]() трехдиагональная матрица жесткости:
трехдиагональная матрица жесткости:

Вектор правых частей системы определяется по формулам:
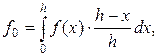


Развернутый вид системы (7) для ![]() уравнений [7, с. 8]:
уравнений [7, с. 8]:

Решение системы находим методом прогонки.
В случае если к концам ![]() приложена вертикальная сила, то краевые условия принимают вид:
приложена вертикальная сила, то краевые условия принимают вид:
 . (8)
. (8)
Условием разрешимости задачи (1), (8) является [2, с. 180]:
 .
.
Вид функционала в соответствующей задаче минимизации:


Окончательно получаем:
 . (9)
. (9)
После подстановки в (9) линейной комбинации (5) получим:
 .
.
Далее, приравнивая вариацию функционала к нулю,
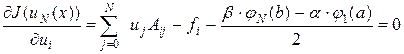 ,
,
получаем систему уравнений [7, с. 8]:
 . (10)
. (10)
При решении системы применяется методом прогонки.
Результаты численных расчетов.
В результате реализации описанного алгоритма для задачи Неймана с однородными краевыми условиями на ![]() с правой частью
с правой частью ![]() получено приближенное решение, график которого изображен на рисунке 1.
получено приближенное решение, график которого изображен на рисунке 1.

Рисунок 1. График решения задачи (1), (2).
Задача Неймана на ![]() с правой частью
с правой частью ![]() и краевыми условиями
и краевыми условиями  имеет приближенное решение, график которого имеет вид:
имеет приближенное решение, график которого имеет вид:
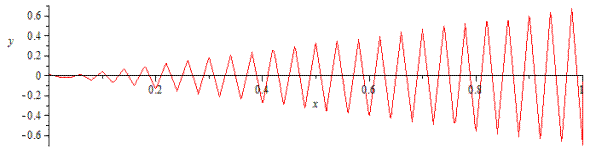
Рисунок 2. График решения задачи (1), (8).
Теперь рассмотрим физическую интерпретацию задачи Неймана для случая ![]() . Пусть на мембрану оказывает действие внешняя сила, плотность которой в каждой точке равна
. Пусть на мембрану оказывает действие внешняя сила, плотность которой в каждой точке равна ![]() и ее направление перпендикулярно плоскости
и ее направление перпендикулярно плоскости ![]() . В состоянии покоя мембрана имеет форму плоской области
. В состоянии покоя мембрана имеет форму плоской области ![]() с границей
с границей ![]() , которая расположена в
, которая расположена в ![]() .
.
Под действием этой силы мембрана прогнется в виде поверхности, уравнение которой ![]() . В положении равновесия функция
. В положении равновесия функция ![]() в каждой внутренней точке
в каждой внутренней точке ![]() удовлетворяет уравнению Пуассона:
удовлетворяет уравнению Пуассона:
![]() , (11)
, (11)
где оператор  .
.
Рассмотрим следующие варианты граничных условий, то есть связей, допускающих перемещение мембраны и относящиеся обычно к краю мембраны [3, с. 36]:
1. Кривая ![]() свободно перемещается вертикально по боковой поверхности цилиндра с основанием
свободно перемещается вертикально по боковой поверхности цилиндра с основанием ![]() , то есть условия на границе имеют вид:
, то есть условия на границе имеют вид:
![]() , (12)
, (12)
где ![]() единичный вектор внешней нормали к
единичный вектор внешней нормали к ![]() . Условия (12) относятся к естественными краевыми условиями [1, с. 10].
. Условия (12) относятся к естественными краевыми условиями [1, с. 10].
2. Помимо внешней силы, к границе приложена вертикальная сила ![]() , тогда получаем граничные условия вида:
, тогда получаем граничные условия вида:
![]() . (13)
. (13)
Классическое решение задачи Неймана из пространства функций ![]() [4, c. 170].
[4, c. 170].
Аналогично одномерному случаю задачи Неймана, в задаче с однородными краевыми условиями (11), (12) на правую часть накладывается условие ![]() и для обеспечения положительной определенности оператора
и для обеспечения положительной определенности оператора ![]() должно выполняться условие для решения:
должно выполняться условие для решения:
![]() .
.
Положительная определенность оператора позволяет перейти от краевой задачи (11), (12) к задаче минимизации функционала:
 . (14)
. (14)
Функция ![]() , реализующая минимум функционала (14) — есть обобщенное решение задачи (11),(12) [4, c. 172]. Пространство
, реализующая минимум функционала (14) — есть обобщенное решение задачи (11),(12) [4, c. 172]. Пространство ![]() это пространство функций, таких, что
это пространство функций, таких, что
 ,
,
где ![]() и
и  обобщенные производные [5, с. 34].
обобщенные производные [5, с. 34].
Слабое решение задачи (11), (13) реализует минимум функционала:
 . (15)
. (15)
где ![]() .
.
Рассмотрим аппроксимацию этих задач методом конечных элементов на прямоугольной области ![]() . Для перехода от непрерывной задачи к конечномерной проведем триангуляцию области (рис. 3) с шагами
. Для перехода от непрерывной задачи к конечномерной проведем триангуляцию области (рис. 3) с шагами  и
и  , а
, а ![]() и
и ![]() — количество разбиений по переменным
— количество разбиений по переменным ![]() и
и ![]() соответственно.
соответственно.

Рисунок 3. Триангуляция прямоугольной области с выделенным носителем ![]() базисной функции
базисной функции ![]() .
.
Приближенное решение ![]() ищем в виде линейной комбинации:
ищем в виде линейной комбинации:
 (16)
(16)
где: ![]() — кусочно-линейные финитные функции, заданные в узлах триангуляции с носителями
— кусочно-линейные финитные функции, заданные в узлах триангуляции с носителями ![]() (рис. 3) [1, с. 184]. После подстановки (16) в (15) получаем:
(рис. 3) [1, с. 184]. После подстановки (16) в (15) получаем:
 , (17)
, (17)
где  ,
,  и
и  ,
,
![]() .
.
Аппроксимация функционала (14) имеет вид:
 . (18)
. (18)
Находим вариацию функционала (17) и приравниваем ее к нулю:
 .
.
Получили систему линейных уравнений:
 , (19)
, (19)
где ![]() для задачи (11), (13), а для задачи (11), (12) —
для задачи (11), (13), а для задачи (11), (12) — ![]() .
.
Систему (19) решаем методом Зейделя.
Результаты численных расчетов.
Описанный алгоритм был реализованы на квадрате ![]() , где
, где ![]() . В таблице 1 приведены результаты работы программ, где
. В таблице 1 приведены результаты работы программ, где ![]() — количество итераций,
— количество итераций, ![]() — заданная точность. Для нахождения решений систем уравнений был использован метод Зейделя.
— заданная точность. Для нахождения решений систем уравнений был использован метод Зейделя.
Таблица 1.
Результаты расчетов задачи Неймана
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Рисунок 4. График решения задачи Неймана с однородными краевыми условиями
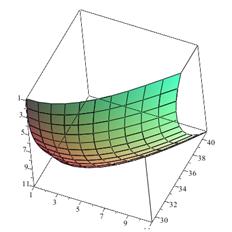
Рисунок 5. График решения задачи Неймана с неоднородными краевыми условиями
Список литературы:
1.Марчук Г.И., Агошков В.И. Введение в проекционно-сеточные методы. М.: Наука. Главная редакция физико-математической литературы, 1981. — 416 с.
2.Марчук Г.И. Методы вычислительной математики. М.: Наука. Главная редакция физико-математической литературы, 1977, — 456 с.
3.Масленникова В.Н. Дифференциальные уравнения в частных производных: Учебник. М.: Изд-во РУДН, 1997. — 447 с.
4.Михайлов В.П. Дифференциальные уравнения в частных производных. М.: Наука, Главная редакция физико-математической литературы, 1976. — 392 с.
5.Михлин С.Г. Линейные уравнения в частных производных. Учеб.пособие для вузов. М., «Высш. школа», 1977. — 431 с.
6.Михлин С.Г. Вариационные методы в математической физике. М.: Наука. Главная редакция физико-математической литературы, 1970. — 512 с.
7.Хабибулина Т.В, Бабинер Е.С. Генерация систем уравнений при решении одномерных задач Дирихле и Неймана методом конечных элементов. / Молодежный научный форум: Естественные и медицинские науки. Электронный сборник статей по материалам IV студенческой международной заочной научно-практической конференции. Москва: Изд. «МЦНО». — 2013. — 44 с. — № 4 (4) / [Электронный ресурс] — Режим доступа. — URL: http://www.nauchforum.ru/archive/MNF_nature/4(4).pdf
дипломов


Оставить комментарий