Статья опубликована в рамках: XVI Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 05 марта 2014 г.)
Наука: Математика
Секция: Дифференциальные уравнения, динамические системы и оптимальное управление
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПОПУЛЯЦИОННОЙ ВОЛНЫ
Колпак Евгений Петрович
д-р физ.-мат. наук, профессор Санкт-Петербургского государственного университета, РФ, г. Санкт-Петербург
E -mail: petrovich_pmpu@mail.ru
Горбунова Екатерина Андреевна
аспирант Санкт-Петербургского государственного университета, РФ, г. Санкт-Петербург
E -mail: katzah428@mail.ru
Жукова Ирина Валерьевна
аспирант Санкт-Петербургского государственного университета, РФ, г. Санкт- Петербург
E-mail:
MATHEMATICAL MODEL OF POPULATION WAVES
Eugeniy Kolnak
doctor of Physics and Mathematics, professor of St. Petersburg State University, Russia St. Petersburg
Catherine Gorbunova
post-graduate student of St. Petersburg State University, Russia St. Petersburg
Irina Zhukova
post-graduate student of St. Petersburg State University, Russia St. Petersburg
АННОТАЦИЯ
Для нелинейного уравнения диффузии, описывающего распространение одиночной популяции на прямой, найдены условия, при которых уравнение может иметь автоволновые решения на бесконечной и полуограниченных прямых. Разработан алгоритм численного построения таких решений, реализованный при построении численного решения конкретных задач.
ABSTRACT
For a nonlinear diffusion equation describing the propagation of a single population at the direct, conditions are found under which the equation may have autowave solution of the infinite and semi bounded direct. The algorithm of the numerical constructing of such series, implemented with the construction of the numerical solution of specific tasks.
Ключевые слова: математическое моделирование; дифференциальные уравнения
Keywords: mathematical modeling; differential equations.
Первые теоретически обоснованные подходы, используемые при разработке математических моделей взаимодействующих популяций, стали интенсивно разрабатываться в первой половине XX века. В работах Вольтера модели динамики взаимодействующих популяций, представлены задачами Коши для систем обыкновенных дифференциальных уравнений [1, 3, 5, 12, 22, 23]. Эти модели предполагают, что свойства среды и плотность популяции не зависят от пространственных координат. Реальные популяции существуют на ограниченных территориях и в ограниченных пространственных объемах с различными свойствами среды в разных ее частях. Распространение их по территории происходит, как правило, от мест с большей концентрацией особей в места с меньшей их концентрацией [6, 10, 24, 25, 35, 41]. Процесс распространения популяции на территории рассматривается, как правило, как случайное индивидуальное или групповое перемещение особей. Математические модели в этом случае разрабатываются на основе аппарата уравнений в частных производных [4, 7, 9, 19, 20, 21, 34, 36, 40, 42, 44, 47, 48—50].
Математическая модель процесса рождения и гибели особей в изолированной популяции на неограниченном трофическом ресурсе в большинстве исследовательских работ представлена начально-краевой задачей для нелинейного дифференциального уравнения в частных производных, которое может иметь неединственное решение [9]. Для случая бесконечной прямой могут существовать и решения типа «бегущая волна» (автоволна), существование которых впервые было доказано в [19]. В работе рассматривается модель одиночной обобщенной популяции, в которой учитывается нелинейность «диффузии» особей и нелинейность скорости их перемещения по территории. Найдены необходимые условия существование решения типа «бегущая волна», предлагается алгоритм построения такого решения.
Математическая модель обобщенной логистической популяции с ограниченным ростом ее численности была предложена в [36]. Динамика численности такой популяции описывается обыкновенным дифференциальным уравнением
![]()
где непрерывная и дважды дифференцируемая функция ![]() удовлетворяет следующим условиям:
удовлетворяет следующим условиям:
![]() (
(![]() ),
),
![]() и
и ![]() ,
,
![]() для
для ![]() .
.
Функция ![]() называется локальной скоростью роста популяции,
называется локальной скоростью роста популяции, ![]() — мультизианским параметром,
— мультизианским параметром, ![]() — емкостью среды [1, 3, 34, 36].
— емкостью среды [1, 3, 34, 36].
Условие ![]() естественное, поскольку в отсутствие особей популяция возникнуть не может, условие
естественное, поскольку в отсутствие особей популяция возникнуть не может, условие ![]() обеспечивает рост возникшей популяции, а условие
обеспечивает рост возникшей популяции, а условие ![]() — ограниченность численности популяции сверху. Стационарная точка
— ограниченность численности популяции сверху. Стационарная точка ![]() является неустойчивой, а точка
является неустойчивой, а точка ![]() — устойчивой. Поэтому все решения уравнения (1) при выполнении условий (2) будут монотонно возрастающими на промежутке
— устойчивой. Поэтому все решения уравнения (1) при выполнении условий (2) будут монотонно возрастающими на промежутке ![]() , выходить из точки
, выходить из точки ![]() и стремиться к значению
и стремиться к значению ![]() при
при ![]() . В дальнейшем за единицу измерения численности популяции принимается емкость среды, т. е.
. В дальнейшем за единицу измерения численности популяции принимается емкость среды, т. е. ![]() . Примерами моделей обобщенной логистической популяции являются логистическая —
. Примерами моделей обобщенной логистической популяции являются логистическая — ![]() , Розенцвейга —
, Розенцвейга — ![]() .
.
В природе в качестве примеров протяженных в одном направлении ареалов, в которых живут различные виды флоры и фауны, могут служить обочины полей и дорог, трубопроводы, реки и т. п. [6, 10, 24, 25, 35, 41]. В модели этот тип распространения популяции можно рассматривать как распространение популяции вдоль прямой. В этом случае процесс распространения особей можно описать эволюционным уравнением [34, 36, 40, 47]
![]()
где: ![]() — декартова координата,
— декартова координата,
![]() параметр, характеризующий подвижность особей, а функция
параметр, характеризующий подвижность особей, а функция ![]() соответствует локальной скорости изменения численности популяции.
соответствует локальной скорости изменения численности популяции.
Для случая отрезка конечной длины к уравнению (3) добавляются граничные условия. Для случая бесконечной прямой это уравнение может иметь автоволновое решение [19, 36, 42, 47] – ![]() (
(![]() — скорость распространения волны). Задача о существовании популяционной волны для одиночной популяции на бесконечной прямой решалась в [19, 34, 36, 40, 42, 47, 50]. В этих работах построено численное решение для уравнения Колмогорова-Пискунова [19] без описания алгоритма его построения. Оценка скорости, с которой волна может двигаться, была дана в работах [19, 36, 47]. Решение уравнения (3) на бесконечной прямой для обобщенной логистической популяции ищется в виде
— скорость распространения волны). Задача о существовании популяционной волны для одиночной популяции на бесконечной прямой решалась в [19, 34, 36, 40, 42, 47, 50]. В этих работах построено численное решение для уравнения Колмогорова-Пискунова [19] без описания алгоритма его построения. Оценка скорости, с которой волна может двигаться, была дана в работах [19, 36, 47]. Решение уравнения (3) на бесконечной прямой для обобщенной логистической популяции ищется в виде ![]() . При этом оно должно удовлетворять условиям
. При этом оно должно удовлетворять условиям
![]() .
.
Такое решение уравнения (3) может существовать, в том случае, если выполняется неравенство [36]
 .
.
Распространение особей на территории не всегда можно рассматривать как случайное блуждание, описываемого в первом приближении уравнением (3). Можно выделить такие механизмы распространения как вытеснение с территории особей низкого социального ранга и расселение особей чувствительных к росту плотности популяции и стремящих занимать участки с минимальной плотностью [6, 10, 24, 25, 35, 41]. Эти два механизма предлагается учесть в модели, представленной дифференциальным уравнением Бюргерса
![]() .
.
В этом уравнении введением функции ![]() учитывается зависимость подвижности особей от локальной плотности популяции (механизм вытеснения особей). Слагаемое
учитывается зависимость подвижности особей от локальной плотности популяции (механизм вытеснения особей). Слагаемое ![]() учитывает «нелинейность» направленного ухода особей с занимаемой территории (самостоятельный уход особей с постоянных участков обитания).
учитывает «нелинейность» направленного ухода особей с занимаемой территории (самостоятельный уход особей с постоянных участков обитания).
Как следует из экспериментальных данных [10, 25, 41, 47] подвижность особей увеличивается с ростом плотности популяции. Поэтому функция ![]() должна быть положительной и возрастающей функцией своего аргумента. В работах Д. Марри [47] предлагается считать
должна быть положительной и возрастающей функцией своего аргумента. В работах Д. Марри [47] предлагается считать ![]() , где
, где ![]() и
и ![]() — положительные параметры, характеризующие подвижность особей. Однако, как следует из анализа экспериментальных данных [10, 25, 41], процесс распространения особей на территории начинается сразу после начала размножения: трофический ресурс в одной точке пространства две особи одновременно использовать не могут. С другой стороны сами особи имеют определенные физические размеры и их нельзя поместить в одно точку пространства. Т. е., процесс случайного перемещения особей в поисках трофического ресурса и естественного «удаления» особей друг от друга начинается одновременно с зарождением популяции. Поэтому в дальнейшем считается, что
— положительные параметры, характеризующие подвижность особей. Однако, как следует из анализа экспериментальных данных [10, 25, 41], процесс распространения особей на территории начинается сразу после начала размножения: трофический ресурс в одной точке пространства две особи одновременно использовать не могут. С другой стороны сами особи имеют определенные физические размеры и их нельзя поместить в одно точку пространства. Т. е., процесс случайного перемещения особей в поисках трофического ресурса и естественного «удаления» особей друг от друга начинается одновременно с зарождением популяции. Поэтому в дальнейшем считается, что ![]() .
.
Автоволновое решение ![]() , где
, где ![]() , уравнения (5) при условиях (4) на бесконечной прямой (
, уравнения (5) при условиях (4) на бесконечной прямой (![]() ) должно удовлетворять уравнению
) должно удовлетворять уравнению
![]() .
.
Для того чтобы существовало решение «бегущая волна», удовлетворяющее условиям (4), необходимо чтобы выполнялись условия
![]() и
и ![]() .
.
При ![]() и
и ![]() уравнение (6) тождественно удовлетворяется. В окрестности точки
уравнение (6) тождественно удовлетворяется. В окрестности точки ![]() решение уравнения (6) представляется в виде
решение уравнения (6) представляется в виде ![]() , где
, где ![]() — малая по сравнению с единицей величина. С учетом этого линеаризация уравнения (6) в окрестности этой точки приводит к уравнению для
— малая по сравнению с единицей величина. С учетом этого линеаризация уравнения (6) в окрестности этой точки приводит к уравнению для ![]()
 .
.
Характеристический полином этого уравнения

имеет вещественные корни противоположных знаков. Поэтому в окрестности этой точки можно построить решение ![]() такое, что
такое, что ![]() при
при ![]() .
.
В окрестности точки ![]() из (6) следует уравнение для малых возмущений
из (6) следует уравнение для малых возмущений ![]()
 .
.
Если ![]() , то собственными значениями характеристического полинома
, то собственными значениями характеристического полинома

Будут
 .
.
Корни характеристического полинома не должны быть комплексно сопряженными, поскольку в этом случае осциллирующее в окрестности точки ![]() решение будет принимать отрицательные значения. Для построения возрастающего решения в окрестности этой точки необходимо чтобы хотя бы один из корней был положительным. Поскольку
решение будет принимать отрицательные значения. Для построения возрастающего решения в окрестности этой точки необходимо чтобы хотя бы один из корней был положительным. Поскольку ![]() положительная величина, то корни будут положительными, если выполняется условие
положительная величина, то корни будут положительными, если выполняется условие
 .
.
При ![]() этот результат согласуется с результатом, приведенным в [19, 36, 42].
этот результат согласуется с результатом, приведенным в [19, 36, 42].
Решение уравнения (6) для полубесконечной прямой ![]() вида
вида ![]() должно удовлетворять уравнению
должно удовлетворять уравнению
![]()
При ![]() функция
функция ![]() должна быть возрастающей. Поэтому решение уравнения (6) с начальными условиями
должна быть возрастающей. Поэтому решение уравнения (6) с начальными условиями
![]()
должно быть положительным и стремиться к нулю при ![]() .
.
В окрестности точки ![]() (при
(при ![]() ) в первом приближении решение можно представить в виде
) в первом приближении решение можно представить в виде ![]() , где
, где ![]() — малая по сравнению с единицей величина. Тогда уравнение (6) в окрестности этой точки с точностью до величин второго порядка малости принимает вид
— малая по сравнению с единицей величина. Тогда уравнение (6) в окрестности этой точки с точностью до величин второго порядка малости принимает вид
 .
.
Решение этого уравнения представляется в виде
![]() ,
,
где

· корни квадратного уравнения
 .
.
Оба корня будут отрицательными, если выполняется неравенство
 .
.
Это условие и является необходимым условием стремления функции ![]() к нулю на бесконечности и, соответственно необходимым условием существования автоволны.
к нулю на бесконечности и, соответственно необходимым условием существования автоволны.
Построение автоволнового решения на бесконечной прямой не представляется возможным. Для случая построения решения на отрезке конечной длины ![]() к уравнению (6) необходимо добавить граничные условия
к уравнению (6) необходимо добавить граничные условия
![]() ,
, ![]() .
.
При этих граничных условиях решениям краевой задачи будут функции ![]() и
и ![]() и, соответственно, краевая задача будет иметь неединственное решение.
и, соответственно, краевая задача будет иметь неединственное решение.
Один из вариантов построения решения — сведение решения краевой задачи (6) и (4) к решению задачи Коши методами типа Рунге-Кутты высокого порядка [11, 13, 28—33, 43] с начальными условиями
![]() ,
, ![]() ,
,
где ![]() и
и ![]() с последующим поиском значений
с последующим поиском значений ![]() и
и ![]() , которые бы обеспечивали близость функции
, которые бы обеспечивали близость функции ![]() к единице при
к единице при ![]() , не дадут результата, поскольку в окрестности точек
, не дадут результата, поскольку в окрестности точек ![]() и
и ![]() решение задачи Коши будет неустойчивым.
решение задачи Коши будет неустойчивым.
При сведении построения решения краевой задачи к решению задачи минимизации функционала

с использованием степенных рядов и методов минимизации функционалов [14—18, 26, 27, 37, 38] также не приведет к результату в силу не единственности решения краевой задачи.
В работе использовался следующий алгоритм построения решения. Численное решение строится на двух промежутка конечной длины: ![]() и
и ![]() . На промежутке
. На промежутке ![]() удовлетворяются граничные условия
удовлетворяются граничные условия
![]() ,
, ![]() (
(![]() ),
),
а на промежутке ![]() условия
условия
![]() ,
,![]() .
.
Затем эти два решения «сшиваются» таким образом, чтобы выполнялось условие:
![]() ,
,
которое рассматривается как нелинейное уравнение относительно ![]() . Поиск корня этого уравнения осуществляется методом Ньютона.
. Поиск корня этого уравнения осуществляется методом Ньютона.
Поскольку уравнение (6) является нелинейным, то для построения его решения использовался метод простой итерации [8, 9]. На каждом итерационном шаге решалось линейное уравнение (![]() — номер итерации)
— номер итерации)
 ,
,
с известной функцией ![]() , взятой с предыдущего итерационного шага. Решение считалось построенным, если выполнялось неравенство
, взятой с предыдущего итерационного шага. Решение считалось построенным, если выполнялось неравенство ![]() , где
, где ![]() — малая величина.
— малая величина.
На каждом из промежутков ![]() и
и ![]() уравнение (7) аппроксимировалось конечными разностями [4, 8, 20, 39, 45—46, 48—50] на равномерной сетке с шагом
уравнение (7) аппроксимировалось конечными разностями [4, 8, 20, 39, 45—46, 48—50] на равномерной сетке с шагом ![]() , где
, где ![]() — число отрезков разбиения интервалов интегрирования. В результате решение краевой задачи сводилось к поиску решения системы нелинейных уравнений
— число отрезков разбиения интервалов интегрирования. В результате решение краевой задачи сводилось к поиску решения системы нелинейных уравнений
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() для отрезка
для отрезка ![]()
и
![]() ,
, ![]() для отрезка
для отрезка ![]() .
.
На каждом итерационном шаге ((7)) система алгебраических уравнений является нелинейной, ее можно построить методом прогонки [8, 39]. Численная реализация осуществлялась в среде программировании пакета MatLab [2].
Некоторые из результатов численного моделирования представлены на рис. 1—3. На рис. 1 приведена зависимость ![]() , построенная на «бесконечной» прямой для случаев, когда
, построенная на «бесконечной» прямой для случаев, когда ![]() и
и ![]() (
(![]() ,
, ![]() ). На рис. 2 — форма автоволны, построенная на полубесконечной прямой для случаев
). На рис. 2 — форма автоволны, построенная на полубесконечной прямой для случаев ![]() при
при ![]() , а на рис. 3 отображена зависимость максимальной амплитуды автоволны от
, а на рис. 3 отображена зависимость максимальной амплитуды автоволны от ![]() при
при ![]() .
.
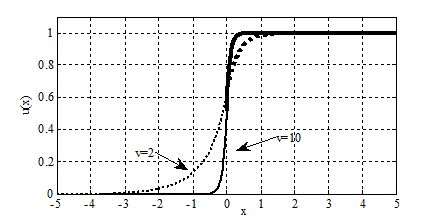
Рисунок 1. Форма автоволны логистической популяции на «бесконечной» прямой при ![]() и
и ![]()

Рисунок 2. Форма автоволны логистической популяции на полубесконечной прямой при ![]() для случая
для случая ![]()

Рисунок 3. Зависимость максимальной амплитуды автоволны на полубесконечной прямой от ![]() для случая
для случая ![]()
Как следует из полученных выше результатов из «диффузионной» модели одиночной популяции следуют результаты, не содержащиеся в «точечных» моделях. Для обобщенной логистической популяции как на бесконечной прямой, та и на полуограниченной, могут существовать автоволновые решения. Скорость движения такой волны зависит от удельной скорости роста численности популяции и от подвижности особей: чем выше удельная скорость роста численности популяции или их подвижность, тем с большей скоростью автоволна должна распространяться.
Список литературы:
1.Александров А.Ю., Платонов А.В., Старков В.Н., Степенко Н.А. Математическое моделирование и исследование устойчивости биологических сообществ. СПб.: Соло, 2006. — 186 с.
2.Андрамонов М.Ю., Тамасян Г.Ш. Реализация аналитического кодифференцирования в пакете matlab // Вычислительные методы и программирование: новые вычислительные технологии. — 2007. — Т. 8. — № 2. — С. 1—5.
3.Базыкин А.Д. Нелинейная динамика взаимодействующих популяций. Москва-Ижевск: Институт компьютерных технологий, 2003. — 368 с.
4.Балыкина Ю.Е., Колпак Е.П Математические модели функционирования фолликула щитовидной железы ./ Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2013. — № 3. — С. 20—31.
5.Вольтерра В. Математическая теория борьбы за существование. Москва-Ижевск:, Институт компьютерных технологий, 2004. — 288 с.
6.Гилев А.В. Закономерности пространственного распределения и научные основы охраны рыжих лесных муравьев // Зоологический журнал. — 2010. — Т. 89. — № 12. — С. 1413—1420.
7.Глызин С.Д. Разностная аппроксимация уравнения «реакция — диффузия» на отрезке // Моделирование и анализ информационных систем. — 2009. — Т. 16. — № 3. — С. 96—116.
8.Годунов С.К., Рябенький В.С. Разностные схемы (введение в теорию). М.: Наука, 1973. — 400 с.
9.Горбунова Е.А., Колпак Е.П. Математические модели одиночной популяции // Вест. С.-Петерб. ун-та. Сер. 10. — 2012. — Вып. 4. — С. 18—30.
10.Громов В.С. Пространственно-этологическая структура популяций грызунов. М.: Т-во научн. изданий КМК. 2008. — 581 с.
11.Еремин А.С., Олемской И.В. Вложенный метод интегрирования систем структурно разделенных обыкновенных дифференциальных уравнений // Журнал вычислительной математики и математической физики. — 2010. — Т. 50. — № 3. — С. 434—448.
12.Жукова И.В., Колпак Е.П Математическая модель солидной опухоли // Естественные и математические науки в современном мире. — 2013. — № 13. — С. 18—25.
13.Кабриц С.А. Мальков В.М., Мансурова С.Е. Математическое моделирование нелинейной деформации эластомерного слоя // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2011. — № 3. — С. 56—63.
14.Карелин В.В Один подход к задаче оценки параметров динамической системы в условиях неопределенности // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2012. — № 4. — С. 31—36.
15.Карелин В.В Точные штрафы в задаче наблюдения // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2008. — № 4. — С. 3—8.
16.Карелин В.В Точные штрафы в многоточечной задаче для обыкновенных дифференциальных уравнений // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2009. — № 4. — С. 104—109.
17.Карелин В.В. Точные штрафы в задаче оценки координат динамической системы в условиях неопределенности // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2011. — № 4. — С. 40—46.
18.Карелин В.В. Штрафные функции в задаче управления процессом наблюдения // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2010. — № 4. — С. 109—114
19.Колмогоров А.Н., Петровский И.Г., Пискунов Н.С. Исследование уравнения диффузии, соединенной с возрастанием количества вещества, и его применение к одной биологической проблеме // Бюл. МГУ. Сер. А. Матеем. и мех. — 1937. — Т. 1. — Вып. 1. — С. 1—26.
20.Колобов А.В., Полежаев А.А. Влияние случайной подвижности злокачественных клеток на устойчивость фронта опухоли // Компьютерные исследования и моделирование. — 2009. — Т. 1. — № 2. — С. 225—332.
21.Колпак Е.П., Балыкина Ю.Е., Котина Е.Д., Жукова И.В. Математическая модель нарушений функционирования щитовидной железы // Молодой Ученый. — 2014. — № 2(61). — С. 19—24.
22.Колпак Е.П., Горбунова Е.А., Балыкина Ю.Е., Гасратова Н.А. Математическая модель одиночной популяции на билокальном ареале // Молодой ученый. — 2014. — № 1 (6). — С. 28—33.
23.Колпак Е.П., Столбовая М.В. Математическая модель кинетики роста растений // Журнал научных публикаций аспирантов и докторантов. — 2013. — № 12 (90). — С. 230—232.
24.Коробченко М.А. Расширение ареала крота европейского (talpa europaea) в долине реки Северный Донец // Зоологический журнал. — 2009. — Т. 88. — № 4. — С. 465—472.
25.Лидерман Г.В., Абатуров Б.Д., Быков А.В., Лопушков В.А. Динамика населения позвоночных животных Заволжской полупустыни. М.: Наука, 2005. — 252 с.
26.Матросов А.В. Вычислительная неустойчивость алгоритма метода начальных функций // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. —2010. — № 4. — С. 30—39.
27.Матросов А.В. Сходимость степенных рядов в методе начальных функций // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2012. — № 1. — С. 41—51.
28.Олемской И.В Конструирование явных методов типа Рунге Кутта интегрирования систем специального вида // Известия высших учебных заведений. Математика. — 2005. — № 2. — С. 75—80.
29.Олемской И.В Структурный подход в задаче конструирования явных одношаговых методов // Журнал вычислительной математики и математической физики. — 2003. — Т. 43. — № 7. — С. 961—974.
30.Олемской И.В. Вложенный пятиэтапный метод пятого порядка типа Дормана-Принса // Журнал вычислительной математики и математической физики. — 2005. — Т. 45. — № 7. — С. 1181—1191
31.Олемской И.В. Метод типа Рунге — Кутты интегрирования систем и дифференциальных уравнений второго порядка специального вида // Вычислительные технологии. — 2004. — Т. 9. — № 2. — С. 67—81.
32.Олемской И.В. Четырехэтапный метод пятого порядка точности численного интегрирования систем специального вида //Журнал вычислительной математики и математической физики. — 2002. — Т. 42. — № 8. — С. 1179.
33.Олемской И.В. Явный метод типа Рунге — Кутты пятого порядка // Вычислительные технологии. — 2005. — Т. 10. — № 2. — С. 87—105.
34.Ризниченко Г.Ю., Рубин А.Б. Биофизическая динамика продукционных процессов. Москва-Ижевск: Институт компьютерных технологий, 2004. — 464 с.
35.Садыков О.Ф., Бененсон И.Е. Динамика численности мелких млекопитающих: Концепции, гипотезы, модели. М.: Наука, 1992. — 191 с.
36.Свирежев Ю.М. Нелинейные волны, диссипативные структуры и катастрофы в экологии. М: Наука, 1987. — 368 с.
37.Тамасян Г.Ш Градиентные методы в вариационной задаче со свободными концами //Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2012. — № 4. — С. 77—84
38.Тамасян Г.Ш Градиентные методы решения задачи коши // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2009. — № 4. — С. 224—230.
39.Тихонов А.Н., Самарский А.А. Уравнение математической физики. М.: Наука, 1972. — 735 с.
40.Тютюнов Ю.В. Пространственная модель развития устойчивости насекомых-вредителей к трансгенной инсектицидной сельскохозяйственной культуре // Биофизика. — Т. 52. — № 1. — С. 95—113.
41.Шиятов С.Г., Терентьев М.М., Фомин В.В., Циммерман Н.Е. Вертикальный и горизонтальный сдвиги верхней границы редколесий и сомкнутых лесов в XX столетии на полярном Урале // Экология. — 2007. — № 4. — С. 243—48.
42.Coville J., Dupaigne L. Propagation speed of travelling fronts in non local reaction–diffusion equations // Nonlinear Analysis. — 2005. — V. 60. — P. 797—819.
43.Eremin A.S., Olemskoy I.V. An embedded method for integrating systems of structurally separated ordinary differential equations // Computational Mathematics and Mathematical Physics. — 2010. — Т. 50. — № 3. — С. 414—427.
44.King J.R., Franks S.J. Mathematical analysis of some multi-dimensional tissue-growth models // Euro. J. of Applied Mathematics. — 2004. — V. 15. — P. 273—295.
45.Mickens R.E. A nonstandard finite difference scheme for a PDE modeling combustion with nonlinear advection and diffusion // Mathematics and computers in simulation. — 2005. — № 69. — P. 439—446.
46.Mickens R.E. A nonstandard finite difference scheme for the diffusionless Burgers equation with logistic reaction // Mathematics and computers in simulation. — 2003. — № 62. — P. 117—124.
47.Murray D.D. Mathematical biology. N.Y. Springer. 2002. — 551 p.
48.Needhamd D.J. On the formation of acceleration and reaction–diffusion wavefronts in autocatalytic-type reaction–diffusion systems // IMA Journal of Applied Mathematics. — 2006. — V. 71. — P. 446—458
49.Schofield P. Spatial explicit models of Turelli-Hoffmann Wolbachia invasive wave fronts // J. Theor. Biol. — 2001. — V. 212. — № 1. — P. 121—131.
50.Yongdong Jin, Jiuping Xu, Wenhua Zhang, Jiuli Luo, Qiwang Xu Simulation of biological waves in single-species bacillus system governed by birth and death-diffusion dynamical equation // Mathematics and Computers in Simulation. — 2005. — V. 68. — P. 317—327.
дипломов


Оставить комментарий