Статья опубликована в рамках: XXVI Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 12 января 2015 г.)
Наука: Математика
Секция: Математическая физика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
ВИХРЕВОЕ РЕШЕНИЕ ДВУМЕРНОГО УРАВНЕНИЯ СИНУС-ГОРДОН
Хусаинова Галина Владимировна
канд. физ.-мат. наук, доцент Уральской государственной архитектурно-художественной академии, РФ, г. Екатеринбург
E -mail: aldisa@mail.ru
Хусаинов Дамир Зиннурович.
канд. физ.-мат. наук, доцент Уральской государственной архитектурно-художественной академии, РФ, г. Екатеринбург
E-mail:
THE VORTEX SOLUTION OF TWO-DIMENSION SINE-GORDON EQUATION
Khusainova Galina
candidate of Science, associate professor of the Ural State Architecture and Art Academy, Russia, Ekaterinburg
Khusainov Damir
candidate of Science, associate professor of the Ural State Architecture and Art Academy, Russia, Ekaterinburg
АННОТАЦИЯ
Рассмотрено вихревое решение (вырожденное солитонное решение) для двумерного уравнения синус-Гордон. Показано, что для ферромагнетика с анизотропией в «легкой плоскости» XY данное решение описывает статическое распределение намагниченности с меньшей энергией, чем в невырожденном случае.
ABSTRACT
The vortex solution (degenerate soliton solution) of two-dimensional sine-Gordon equation was considered. It has been shown that the solution obtained describes for the ferromagnetic with XY “easy plane” anisotropy static magnetization distribution with lower energy then in nondegenerate case.
Ключевые слова: вихрь; солитон; ферромагнетик.
Keywords : vortex; soliton; ferromagnetic.
Энергия ферромагнетика E с любым неоднородным распределением намагниченности записывается как функционал вектора ![]() :
:
 (1)
(1)
индексы i,k принимают значения: i,k=1,2,3, w — плотность электромагнитной энергии, явная запись которой зависит от рассматриваемой модели ферромагнетика [2, с. 9].
Рассмотрим модель ферромагнетика с большой анизотропией по оси Z: ![]() и
и ![]() (
( ![]() — постоянные анизотропии). Тогда в основном состоянии вектор намагниченности
— постоянные анизотропии). Тогда в основном состоянии вектор намагниченности ![]() лежит в “легкой плоскости” XY:
лежит в “легкой плоскости” XY: ![]() . В этом случае плотность свободной энергии имеет вид:
. В этом случае плотность свободной энергии имеет вид:
 (i=1,2), (2)
(i=1,2), (2)
![]() — константа обменного взаимодействия.
— константа обменного взаимодействия.
С учетом (2) уравнение Эйлера-Лагранжа приводит к нелинейному двумерному статическому уравнению синус-Гордон:
![]() ,
, ![]() (3)
(3)
где: ![]() — характерная магнитная длина, связанная с обменным взаимодействием и постоянной анизотропии:
— характерная магнитная длина, связанная с обменным взаимодействием и постоянной анизотропии:  .
.
Запишем уравнение (3) в безразмерных единицах (за единицу длины выбрана длина ![]() ) и сделаем замену
) и сделаем замену ![]() , тогда получим двумерное эллиптическое уравнение синус-Гордон:
, тогда получим двумерное эллиптическое уравнение синус-Гордон:
![]() (4)
(4)
Простейшее вихревое (вырожденное солитонное) решение уравнения (4) имеет вид [4, с. 3; 5, с. 36]:
![]() , (5)
, (5)
![]() (6)
(6)
![]() (7)
(7)
где: ![]() ,
,
![]() — произвольные постоянные. Для удобства вычислений введена параметризация:
— произвольные постоянные. Для удобства вычислений введена параметризация: ![]() , где
, где ![]() — это угол, который образует вектор
— это угол, который образует вектор ![]() с выбранной полярной осью в плоскости XY.
с выбранной полярной осью в плоскости XY.
Решение (5) является вырожденным по параметру ![]() , так как двум магнитным солитонам (
, так как двум магнитным солитонам (![]() -градусным доменным границам) соответствуют два равных по модулю и параллельных вектора
-градусным доменным границам) соответствуют два равных по модулю и параллельных вектора ![]() [4, с. 3]. Такое взаимодействие доменных границ приводит к образованию нового магнитного возбуждения — магнитного вихря в плоскости магнетика. Решения, описывающие топологические дефекты или вихри характеризуются следующим условием:
[4, с. 3]. Такое взаимодействие доменных границ приводит к образованию нового магнитного возбуждения — магнитного вихря в плоскости магнетика. Решения, описывающие топологические дефекты или вихри характеризуются следующим условием:
![]() , (8)
, (8)
где: ![]() — произвольный контур в XY плоскости, окружающий некоторую точку (x 0,y0) — центр вихря, и с обходом, заданным против часовой стрелки,
— произвольный контур в XY плоскости, окружающий некоторую точку (x 0,y0) — центр вихря, и с обходом, заданным против часовой стрелки,
n — любое целое число (топологический заряд вихря) [1, c. 144]. Решения для n>0 называют вихрями, а с n<0 — антивихрями. Статическое распределение намагниченности, соответствующее вихревой конфигурации (9) приведено на Рис. 1. Оно показывает поле направлений вектора ![]() в плоскости XY. Видно, что поле имеет типичную антивихревую структуру.
в плоскости XY. Видно, что поле имеет типичную антивихревую структуру.
Оценим энергию ферромагнетика с таким распределением намагниченности. Пусть ![]() , тогда из (5) получаем:
, тогда из (5) получаем:
![]() . (9)
. (9)
В этом случае магнитная энергия ферромагнетика:
![]() (10)
(10)
(выражения (10) записано в безразмерных единицах). Подставляя (9) в (10) и преобразуя полученное выражение, имеем:
 , (11)
, (11)
где: ![]() — энергия основного состояния ферромагнетика.
— энергия основного состояния ферромагнетика.

Рисунок 1. Векторное поле для ![]() А — антивихрь
А — антивихрь
Выберем область интегрирования, как показано на Рис.2. Проинтегрируем по области I.
 .
.

Рисунок 2. Область интегрирования при вычислении энергии E -E0 по формуле (9)
После интегрирования по x, имеем:
 ,
, ![]() .
.
Поскольку точно проинтегрировать по y выражения не удается, оценим поведение подинтегральных функций в интегралах I1 и I2 при больших R.
В этом случае, получаем:
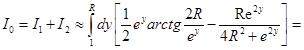
= ![]() (12)
(12)
Проинтегрируем по области II:

После интегрирования по х :

При больших R:
![]() . (13)
. (13)
Таким образом, с учетом формул (12) и (13), находим:
![]() . (14)
. (14)
Результат оценки показывает, что при больших R энергия линейно зависит от размера образца. Сравним наш результат с энергией ферромагнетика, соответствующего вихревому решению Худака, Такено и Ходенкова [6, с. 247; 7, с. 994; 3, с. 647].
 . (15)
. (15)
Аналогичными вычислениями можно показать, что в невырожденном случае энергия ферромагнетика:
![]() . (16)
. (16)
Отметим, что рассмотренный невырожденный случай с распределением намагниченности, задаваемым формулой (15) соответствует случаю, когда доменные границы характеризуются перпендикулярными векторами ![]() и
и ![]() .
.
Из вышеприведенных результатов (14) и (16) следует, что в вырожденном случае, когда вектора ![]() и
и ![]() , характеризующие доменные границы, параллельны, энергия ферромагнетика, хотя и большая (линейная по R), но меньше, чем в невырожденном случае. Таким образом, вихревая конфигурация (9) соответствует меньшему значению энергии по сравнению с вихрем (15).
, характеризующие доменные границы, параллельны, энергия ферромагнетика, хотя и большая (линейная по R), но меньше, чем в невырожденном случае. Таким образом, вихревая конфигурация (9) соответствует меньшему значению энергии по сравнению с вихрем (15).
Список литературы:
1.Борисов А.Б., Танкеев А.П., Шагалов А.Г. Новые типы вихреподобных состояний в магнетиках //ФТТ, — 1989 — Т. 31 — С. 140—147.
2.Косевич А.М., Иванов Б.А., Ковалев А.С. Нелинейные волны намагниченности. Динамические и топологические солитоны. Киев: Наук. Думка, 1983 — 192 с.
3.Ходенков Г.Е. Некоторые точные многомерные решения уравнений Ландау-Лифшица в одноосном ферромагнетике // ФММ, — 1982 — Т. 54, — № 4 — С. 644—649.
4.Хусаинова Г.В. (Безматерных Г.В.), Хусаинов Д.З. Вырожденное солитонное решение двумерного уравнения синус-Гордон //Фундаментальные и прикладные исследования в современном мире: материалы VII Междунар. научно-практической конф. СПб., — 2014 — Т. 1 — С. 32—38.
5.Bezmaternih G.V. (Khusainova G.V.), Borisov A.B. Rational – Exponential Solutions of Nonlinear Equations// Lett.Math.Physics, — 1989 — V. 18 — P. 1—8.
6.Hudak O. On vortex configurations in two — dimensional Sine — Gordon systems with applications to the phase transitions of the Kosterlits — Thoules type and to Josephson junctions // Phys.Lett., — 1982 — V. 89A, — № 5 — P. 245—248.
7.Takeno S. Multi — (Resonant — Soliton) — Solitons and Vortex — like Solutions to Two — and Three — Dimensional Sine — Gordon Equations // Progr.Theor. Phys. — 1982 — V. 68, — № 3 — P. 992—995.
дипломов


Оставить комментарий