Статья опубликована в рамках: XXVII Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 04 февраля 2015 г.)
Наука: Информационные технологии
Секция: Математическое моделирование, численные методы и комплексы программ
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
ОБ ОДНОЙ ЗАДАЧИ МАРШРУТИЗАЦИИ ТРАНСПОРТА НА ГОРОДСКИХ ТРАНСПОРТНЫХ СЕТЯХ
Попков Владимир Константинович
д-р физ.-мат. наук, профессор, главный научный сотрудник Института вычислительной математики и математической геофизики СО РАН, РФ, г. Новосибирск
Ахмедиярова Айнур Танатаровна
докторант КазНТУ имени К.И. Сатпаева по специальности «Информационные системы», Республика Казахстан, г. Алматы
">ААТ
Куандыкова Джанна Рискуловна
канд. техн. наук, доцент университета «Туран», Республика Казахстан, г. Алматы
ON A PROBLEM OF TRANSPORT ROUTING FOR URBAN TRANSPORT NETWORKS
Popkov Vladimir
Dr., Professor, Senior Researcher, Institute of Computational Mathematics and Mathematical Geophysics SB RAS, Russia, Novosibirsk
Ahmediyarova Aynur
doctoral KazNTU by specialty "Information Systems", Republic of Kazakhstan, Almaty
Kuandykova Gianna
Ph.D., Associate Professor University "Turan", Republic of Kazakhstan, Almaty
АННОТАЦИЯ
Рассматривается работа системы управления маршрутизацией транспорта, проведен обзор теоретической основы маршрутизации для информационных сетей. Даны описания алгоритмов поиска кратчайших путей на графах. Представлена концепция системы управления маршрутизацией транспортных средств для городских транспортных сетей.
ABSTRACT
We consider the work of the routing control of transport, a review of the theoretical basis for the routing information networks. Describes the search algorithms of the shortest paths in graphs. Introduces the concept of routing control vehicles for urban transport networks.
Ключевые слова: потоки машин; управление транспортом; алгоритм управления маршрутизацией.
Keywords : heavy traffic; transportation management; routing control algorithm.
Введение
В настоящее время с ростом населения крупных городов значительно увеличилось число автомобилей на дорогах. Загруженность городских автомагистралей усилилась, также неизбежно выросла вероятность совершения аварии, по вине которой движение замедляется или вообще останавливается. Вместе с тем человек, естественно, желает добраться куда-либо как можно быстрее. Или он просто ездит с работы домой и обратно и не хочет тратить свое время на «стояние» в пробке, или это курьер, или работник экстренной службы, для которого каждая минута на счету.
Одним из выходов может стать система управления маршрутизацией транспорта, владеющая самой свежей информацией о состоянии дорог и способная вычислить кратчайший путь через весь город. Таким образом, автомобилисты смогут избежать пробок и достигнуть места назначения в кратчайшие сроки.
Постановка задачи
Задача маршрутизации транспорта на городских транспортных сетях очень похожа на маршрутизацию компьютерного трафика в сетях информационных. Главные отличия состоят в том, что в первом случае в качестве пакета рассматривается транспортное средство, а также существуют правила дорожного движения, ограничивающие передвижение пакетов. В то же время, задача маршрутизации транспорта состоит все в той же проблеме нахождения кратчайшего пути между двумя узлами.
Рассмотрим идею работы системы управления маршрутизацией транспорта.

Рисунок 1. Работа системы управления маршрутизацией транспорта
На подъездах к перекресткам установлены специальные приемо-передатчики, связанные с центральным сервером. На центральный сервер периодически поступает информация с камер/датчиков, расставленных на дорогах и следящих за состоянием дорожной сети. Эти камеры способны замерять скорость движения потока по участкам дороги. Таким образом, центральный сервер узнает об изменении условий движения на каком-то участке дороги и отправляет соответствующую информацию на приемо-передатчики. Автомобиль оборудован специальной меткой. При подъезде к перекрестку, который является фактически узлом коммутации, приемо-передатчик считывает информацию об автомобиле. Эта информация может быть зашифрована в виде <номер автомобиля, точка назначения>. Затем автомобиль получает направление до следующего узла и продолжает движение.
Как уже было сказано выше, мы будем рассматривать централизованный адаптивный алгоритм управления маршрутизацией, так как это позволяет снизить затраты, поскольку нет необходимости оснащать приемо-передатчики процессорами большой мощности. Также необходимо учитывать задержки при обмене информацией между приемо-передатчиками и центральным сервером. Однако скорость движения автомобилей гораздо меньше скорости распространения элекронного сигнала, так что неприятностей можно избежать, расставив приемо-передатчики соответствующим образом.
Блок-схема работы системы приведена ниже.

Рисунок 2. Блок-схема работы системы
Математическая постановка
Математически задача маршрутизации вообще и транспорта в частности сводится к нахождению кратчайшего пути в (не)ориентированном графе.
Определение: Городская транспортная сеть — ![]() — взвешенный ориентированный граф, где N — множество вершин (перекрестков) А — множество дуг (участков дорог, соединяющих две вершины каждый).
— взвешенный ориентированный граф, где N — множество вершин (перекрестков) А — множество дуг (участков дорог, соединяющих две вершины каждый).
Функция ![]() определяет стоимость каждой дуги
определяет стоимость каждой дуги ![]() . Метрикой в нашем случае является время прохождения пакета по дуге.
. Метрикой в нашем случае является время прохождения пакета по дуге.
Таким образом, целевая функция выглядит следующим образом:
 (1)
(1)
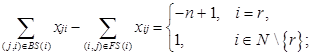 (2)
(2)
Некоторые пояснения.
BS(i) и FS(i) — это соответственно звезды исходящих и входящих путей в вершину i, то есть:

Таким образом, решается целочисленная задача булева линейного программирования — минимизация суммарного времени пути от узла r к узлу i.
Существуют разные алгоритмы решения подобного типа задач.
Метод Дейкстры ( Dijkstra).
Алгоритм Дейкстры — это классический алгоритм для поиска кратчайших путей от одной вершины графа до всех остальных. Пусть ![]() — взвешенный ориентированный граф с неотрицательными весами дуг,
— взвешенный ориентированный граф с неотрицательными весами дуг, ![]() – источник,
– источник, ![]() — сток, и
— сток, и ![]() длина дуги
длина дуги ![]() . Тогда алгоритм выглядит следующим образом:
. Тогда алгоритм выглядит следующим образом:
Алгоритм 1
1. Пусть ![]() пустое множество, и потенциалы
пустое множество, и потенциалы ![]() для каждой вершины
для каждой вершины ![]() , кроме
, кроме ![]() .
.
2. Добавляем к ![]() вершину
вершину ![]() , имеющую минимальный потенциал в
, имеющую минимальный потенциал в ![]() . Если
. Если ![]()
3. Для каждой вершины ![]() такой, что
такой, что ![]() , если
, если ![]() , положить
, положить ![]() и перемещаемся в вершину
и перемещаемся в вершину ![]() (
(![]() ).
).
4. Перейти на шаг 2.
Минимальное время работы алгоритма есть ![]() .
.
Мы написали программу, использующий метод Дейкстры для поиска кратчайшего пути на графе между двумя вершинами.
Алгоритм А*.
А* («А-звёздочка») — это расширение метода Дейкстры, эвристический алгоритм для поиска кратчайшего пути между двумя вершинами. Он использует эвристическое приближение для длины кратчайшего пути от каждой вершины к вершине-назначению. Пусть ![]() — оценщик длины кратчайшего пути между
— оценщик длины кратчайшего пути между ![]() . И пусть
. И пусть ![]() — точка назначения. Тогда алгоритм действует по следующей схеме:
— точка назначения. Тогда алгоритм действует по следующей схеме:
Алгоритм 2
1. Пусть ![]() пустое множество, и потенциалы
пустое множество, и потенциалы ![]() для каждой вершины
для каждой вершины ![]() , кроме
, кроме ![]() .
.
2. Добавляем к ![]() вершину
вершину ![]() , для которой
, для которой ![]() минимально в
минимально в ![]() . Если
. Если ![]() , стоп.
, стоп.
3. Для каждой вершины ![]() , такой, что
, такой, что ![]() , если
, если ![]() , положить
, положить ![]() , перемещаемся в вершину
, перемещаемся в вершину ![]() и удаляем
и удаляем ![]() из
из ![]() , если
, если ![]() .
.
4. Перейти на шаг 2.
Если ![]() удовлетворяет ограничению, что
удовлетворяет ограничению, что ![]() есть нижняя граница
есть нижняя граница ![]() , то полученный путь обязательно будет оптимальным кратчайшим путем.
, то полученный путь обязательно будет оптимальным кратчайшим путем.
![]() (3)
(3)
Следует отметить, что если ![]() , алгоритм А* сразу найдет только дуги на кратчайшем пути от источника к стоку. Более того, удаление вершины из
, алгоритм А* сразу найдет только дуги на кратчайшем пути от источника к стоку. Более того, удаление вершины из ![]() на шаге 3 может быть исключено из алгоритма, если приближение удовлетворяет следующему ограничению, называющемуся монотонным ограничением:
на шаге 3 может быть исключено из алгоритма, если приближение удовлетворяет следующему ограничению, называющемуся монотонным ограничением:
![]() (4)
(4)
В этом случае оценщик называется выполнимым для двойственной задачи (dual feasible estimator). Например, для евклидово расстояния на дорожной сети — оценщик для двойственной задачи выполним, то есть двойственная задача выполнима. Очевидно, что ![]() также удовлетворяет верхнему ограничению. Следует отметить, что число найденных вершин в этом случае всегда не превосходит числа найденных вершин методом Дейкстры. Фактически метод Дейкстры — это метод А*, у которого
также удовлетворяет верхнему ограничению. Следует отметить, что число найденных вершин в этом случае всегда не превосходит числа найденных вершин методом Дейкстры. Фактически метод Дейкстры — это метод А*, у которого ![]() для всех вершин.
для всех вершин.
Двунаправленный метод (The bidirectional Method)
Двунаправленный метод также используется для поиска кратчайшего пути между двумя вершинами графа. Он не требует эвристическую оценку, но может уменьшить число найденных вершин в большинстве случаев. В этом алгоритме поиск ведется не только от источника к стоку, но и в обратную сторону. Алгоритм работает следующим образом:
Алгоритм 3
1. Пусть ![]() и
и ![]() — пустые множества, и пусть потенциалы
— пустые множества, и пусть потенциалы ![]() и
и ![]() равны
равны ![]() для каждой вершины
для каждой вершины ![]() , за исключением
, за исключением ![]() и
и ![]() .
.
2. Добавляем к ![]() вершину
вершину ![]() , которая имеет наименьший потенциал
, которая имеет наименьший потенциал ![]() в
в ![]() . Если
. Если ![]() , перейти на шаг 7.
, перейти на шаг 7.
3. Для каждой вершины ![]() , такой, что
, такой, что ![]() , если
, если ![]() , положим
, положим ![]() и рассматриваем предыдущую
и рассматриваем предыдущую![]() вершину v в качестве
вершину v в качестве ![]() .
.
4. Добавляем к ![]() вершину
вершину ![]() , которая имеет наименьший потенциал
, которая имеет наименьший потенциал ![]() в
в ![]() . Если
. Если ![]() , перейти на шаг 7.
, перейти на шаг 7.
5. Для каждой вершины ![]() , такой, что
, такой, что ![]() , если
, если ![]() , положим
, положим ![]() и рассматриваем предыдущую
и рассматриваем предыдущую![]() вершину v в качестве
вершину v в качестве ![]() .
.
6. Перейти на шаг 2.
7. Найти дугу ![]() , которая имеет наименьшее значение
, которая имеет наименьшее значение ![]() . Кратчайший путь от
. Кратчайший путь от ![]() до
до ![]() состоит из кратчайшего пути от
состоит из кратчайшего пути от ![]() до
до ![]() , дуги
, дуги ![]() и кратчайшего пути от
и кратчайшего пути от ![]() до
до ![]() .
.
Описание работы системы управления маршрутизацией
В данной работе предлагается разбить задачу управления маршрутизацией транспорта на две части: статическую и динамическую.
Статическая часть
Если рассматривать городскую транспортную сеть в виде графа, то появляется проблема, связанная с большой размерностью системы. Облегчить вычислительную задачу может разбиение городской сети на меньшие сегменты, связанные между собой через единственные узлы. То есть такие узлы, которые нельзя миновать при движении из одной точки города в другую. Например, для Новосибирска такими узлами могут быть: мост через Иню, дамба Обь-ГЭС и т.п. При таком разбиении кратчайшие пути не изменятся, так как здесь будет работать принцип оптимальности.
Далее, при первоначальной прокладке маршрута предлагается воспользоваться статистическими данными. Это средние скорости транспортного потока на всех участках дорог в зависимости от дня недели, времени суток, возможно погоды. По этим данным вычисляются веса ребер графа, и кратчайший маршрут вычисляется с помощью любого из алгоритмов поиска кратчайшего пути на графе.
Динамическая часть
В динамической части предполагается собственно управление маршрутизацией транспортных средств центральным сервером в режиме реального времени. При этом предлагается использовать аналог метода рельефов для информационных сетей.
Метод рельефов - это динамический децентрализованный адаптивный алгоритм. Его удобство заключается в том, что при нём пакету дается направление движения к следующему узлу, что очень удобно в случае маршрутизации автомобильного транспорта. Таким образом, водителю транспортного средства будет дана рекомендация по выбору дальнейшего направления. И при подъезде следующего автомобиля не потребуется никаких перевычислений, при условии сохранения тех же параметров пропускной способности дорог.
Заключение
1. В статье был проведен обзор теоретической основы маршрутизации для информационных сетей. Даны описания алгоритмов поиска кратчайших путей на графах и создана программа на основе одного из них.
2. Представлена концепция системы управления маршрутизацией транспортных средств для городских транспортных сетей.
3. Показано, что городская транспортная сеть может быть представлена в виде графа, и теория и методы, посвященные маршрутизации в информационных сетях, могут быть перенесены на транспортные сети. Это является заделом для дальнейших исследований в данной области.
В будущем предполагается:
· Произвести детальное сравнение не только классических, но и имеющихся в настоящее время алгоритмов поиска кратчайших путей на графах.
· Создать централизованный аналог метода рельефов для управления маршрутизацией транспорта в городской дорожной сети.
Список литературы :
1.Крылов Ю.Д. Вычислительные сети // Учебное пособие, Санкт-Петербургский государственный университет аэрокосмического приборостроения, стр. 105—111, СПб 2006.
2.Смелянский Р.Л. Системы передачи данных и сети ЭВМ // лекции ВМИК МГУ.
3.Hector Gonzalez. Adaptive Fastest Path Computation on a Road Network: A Traffic Mining Approach // VLDB ‘07, September 23—28, 2007, Vienna, Austria.
4.Rico Jacob. A Computational Study of Routing Algorithms for Realistic Transportation Networks //ACM
5.Shivaram Subramanian. Routing algorithms for dynamic, intelligent transportation networks, // Dissertation, Virginia Polytechnic Institute and State University, Blacksburg, Virginia, 1997
6.Tetsuo Shibuya. Computing the n*m Shortest Path Effeciently // ALENEX'99, LNCS 1619, pp. 210—224, 1999.
7.Yun-Wu Huang. Query optimization for navigation in geographic information systems // Dissertation, The University of Michigan, 1997.
дипломов


Оставить комментарий