АНАЛИЗ  АВТОКОЛЕБАНИЙ  КОЛЕСНОГО  МОДУЛЯ  ПРИ  ДВУХ  МОДЕЛЯХ  ВЗАИМОДЕЙСТВИЯ  КОЛЕСА  С  ОПОРНОЙ  ПОВЕРХНОСТЬЮ

Вельмагина  Наталья  Александровна

соискатель,  ИПММ  НАН  Украины,  г.  Донецк

E-mail: 

Вербицкий  Владимир  Григорьевич

профессор,  д-р  ф.-  мат.  наук,  ИПММ  НАН  Украины,  г.  Донецк

E-mail: 

Проведен  сравнительный  анализ  двух  моделей  взаимодействия  колеса  с  опорной  поверхностью  в  боковом  направлении  (нелинейной  гипотезы  увода  И.  Рокара  и  неголономной  модели  М.В.  Келдыша,  в  которой  учитывается  нелинейность  боковой  силы)  на  характер  автоколебаний  колесной  сцепки.

Ключевые  слова:  автоколебания,  устойчивость,  колесный  модуль.

Введение.  Явление  шимми  —  это  интенсивные  самовозбуждающиеся  колебания  катящихся  колес,  проявляющиеся  в  виде  крутильных  движений  колес  в  горизонтальной  плоскости  (их  верчения),  которые  сопровождаются  другими  движениями  из  продольной  вертикальной  плоскости  [3,  4]. 

Шимми  элементов  шасси  в  первую  очередь  связано  с  наличием  упругого  пневматика,  который  при  определенных  условиях  «трансформирует»  часть  подводимой  к  транспортному  средству  энергии  в  энергию  крутильных  колебаний  колеса  и  стойки. 

Анализ  условий  возникновения  автоколебаний  был  и  остается  предметом  исследования  многих  авторов  как  представителей  теоретического  направления  [1,  5,  6,  8,  11,  15,  16],  так  и  инженеров-исследователей  авиационного  и  автомобильного  транспорта  [3,  4,  9,  12—14,  17].  При  определении  характеристик  боковой  реакции  упругого  колеса  с  опорной  поверхностью  наибольшее  распространение  получили  две  постановки:  модельная  (теория  М.В.  Келдыша  [5])  и  феноменологическая  (аксиоматика  И.  Рокара  [10]).

В  целом  задачу  о  возникновении  шимми  можно  разбить  на  две  части  —  задачу  определения  границы  устойчивости  в  пространстве  параметров  (линейная  задача)  и  задачу  определения  характеристик  автоколебаний  (амплитуда,  частота),  что  требует  учета  нелинейных  характеристик  взаимодействия. 

В  данной  работе  проведен  сравнительный  анализ  устойчивости  прямолинейного  движения  простейшей  модели  колесной  сцепки  (рояльной  конструкции),  имеющей  свободу  рысканья  относительно  вертикальной  оси,  для  двух  моделей  взаимодействия  колеса  с  опорной  поверхностью  в  боковом  направлении  (нелинейной  гипотезы  увода  И.  Рокара  и  модели  М.В.  Келдыша,  в  которой  учтен  нелинейный  характер  боковой  силы).

Основная  часть.  Уравнения  возмущенного  движения  передней  стойки  в  работе  представлены  для  частного  случая  вертикальной  стойки  шасси  с  целью  получения  обозримых  аналитических  соотношений,  которые  можно  сравнить  с  аналогичными  известными  результатами,  полученными  на  основе  линейных  моделей  взаимодействия  [8]. 

  (1)

В  системе  (1)  представлена  модель  взаимодействия  колеса  с  опорной  поверхностью  по  И.  Рокару  [16].  Первое  уравнение  отвечает  кинематической  связи,  принятой  в  теории  неустановившегося  увода,  здесь  δ  —  угол  увода  колеса  (угол  между  вектором  скорости  центра  колеса  и  продольной  плоскостью  симметрии  колеса);  V  —  скорость  невозмущенного  движения;  σ  —  параметр  релаксации.  Сила  увода    имеет  характер  функции  насыщения,  при  малых  углах  увода  представима  в  виде  линейной  функции  ,  где    —  коэффициент  сопротивления  уводу;    —  стабилизирующий  пяточный  момент,  представлен  в  виде  линейной  функции  угла  увода  .  Конструктивные  параметры  системы:  F  —  момент  инерции  относительно  оси  вращения  стойки,  k  —  коэффициент  демпфирования,  l  —  вынос  колеса,  предполагается  положительным  (вынос  назад),  с  —  крутильная  жесткость  стойки  относительно  вертикальной  оси.

Уравнения  возмущенного  движения  колесной  сцепки,  соответствующие  модели  М.В.  Келдыша  [5,  8],  имеют  вид  (2) 

;

;  (2)

где:  y  —  боковая  деформация  пневматика, 

  —  угловая  деформация  пневматика  (  —  связь  с  углом  увода), 

  —  боковая  сила, 

  —  пяточный  момент.

В  этом  случае  для  описания  модели  требуется  четыре  параметра  a_y  —  коэффициент  жесткости  колеса  в  поперечном  направлении  (  —  поперечная  сила  в  линейном  приближении),  b  –  крутильная  жесткость  колеса  (  —  пяточный  момент  относительно  вертикальной  оси),    —  кинематические  параметры,  входящие  в  уравнения  кинематических  (неголономных)  связей.  Если  формально  принять  соотношение  ,  которое,  вообще  говоря,  справедливо  при  качении  колеса  с  установившимся  уводом,  то  учитывая  соотношение  между  ,  из  физических  соображений  получим    (система  (2)  вырождается  в  систему  (1)).  Как  показано  в  [11],  параметр  релаксации  определяется  отношением  кинематических  параметров    (это  же  соотношение  следует  из  второго  уравнения  системы  (2)  при  предположении  о  реализации  установившегося  увода),  что  дает  возможность  определить  параметры  модели  И.  Рокара  по  параметрам  модели  М.В.  Келдыша.

Далее  учитывая  согласованность  параметров  (,  определим  условия  устойчивости  по  линейному  приближению  систем  (1)  и  (2). 

Граница  области  колебательной  неустойчивости  системы  (1)  задается  соотношением  (3)  (условие  обращения  в  нуль  предпоследнего  определителя  Гурвица),  в  котором  участвует  приведенный  коэффициент  сопротивления  уводу  ,  учитывающий  влияние  пяточного  момента  (формально  соответствует  увеличению  номинального  коэффициента  сопротивления  уводу) 

(3)

Далее  рассмотрены  характерные  особенности  границы  области  устойчивости  в  пространстве  характерных  конструктивных  параметров  системы.  Наличие  положительных  корней  уравнения  (3)  относительно  параметра    свидетельствует  о  наличии  интервала  колебательной  неустойчивости  в  диапазоне  от    до    (,  –  корни  уравнения).  Такой  интервал  может  существовать,  если  коэффициент  при  в  (3)  меньше  нуля  (необходимое  условие  наличия  интервала  колебательной  неустойчивости).  При    или  ,  интервал  колебательной  неустойчивости  отсутствует.

При  l<σ  колебательная  неустойчивость  может  реализовываться  в  интервале  ,  где    и    корни  квадратного  уравнения  .  При  k=0  интервал  колебательной  неустойчивости  реализуется  при  l₁=0,  l₂=σ. 

На  границе  интервала  скорости,  отвечающей  паре  чисто  мнимых  корней,  в  соответствии  с  теоремой  Андронова-Хопфа  происходит  комплексная  бифуркация  (рождения-исчезновения)  предельного  цикла  [7]. 

Представим  результаты  анализа  условий  возникновения  автоколебаний  передней  стойки  шасси  на  основе  приближенного  аналитического  подхода  [2].  Предполагается,  что  периодическое  решение  системы  (1)  в  моменты  наибольшего  отклонения  от  положения  равновесия  и  в  моменты,  когда  отклонения  равны  нулю,  изменяется  по  гармоническому  закону,  имея  некоторое  запаздывание  по  фазе  ,  здесь  а  —  амплитуда,  —  запаздывание  фазы.  В  характерные  моменты  времени  фазовые  переменные  и  их  производные  принимают  значения 

  (4)

В  этом  случае  параметры  автоколебаний  ()  определяются  из  системы  конечных  уравнений,  полученной  после  подстановки  (4)  в  систему  (1)

       (5)

После  исключения  неизвестных  p₀,  φ_ψ  из  первых  двух  уравнений  системы  (5),  получим  соотношения  (6,  7),  которые  определяет  усредненную  частоту  периодического  решения 

;  (6)          

и  его  амплитуду 

,  (7)

где:  нелинейная  функция,  учитывающая  наличие  пяточного  момента.

Заметим,  что  подстановка  в  (7)  линейной  гипотезы  увода  приведет  к  выражению  (3),  определяющему  границы  колебательной  неустойчивости  —  амплитудная  кривая,  примыкающая  к  оси  абсцисс,  соответствует  устойчивым  автоколебаниям,  а  вырезаемый  ею  интервал  на  оси  продольной  скорости  движения  соответствует  области  колебательной  неустойчивости.

Для  системы  (2)  аналогичным  методом  получена  неявная  функция,  определяющая  амплитуды  автоколебаний  по  боковой  деформации  пневматика,  из-за  громоздкости  здесь  не  приводится  (отметим,  что  при  k=0  из  выражения  амплитудной  кривой  следуют  известные  условия  устойчивости  [8])

Нелинейная  зависимость  боковой  силы  аппроксимировалась  дробно  иррациональной  функцией 

  для  системы  (1),    для  системы  (2),

где:  N  —  вертикальная  реакция  опоры, 

  —  коэффициент  сцепления  в  поперечном  направлении. 

Графики  соответствующих  амплитудных  кривых  (см.  рис.  1),  получены  с  помощью  пакета  MAPLE  для  следующего  набора  числовых  значений  параметров:  а_y=98100  Н/м;  ;  b=2943  Н/м;  l=0,25  м;  F  =30  кгм²;  N=5000  Н;  k=57,3  Нмс;  c=0;  α=60  1/м²;  β=20  1/м. 

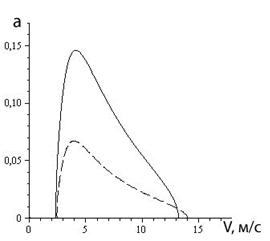
                              а)                                                      б)

Рисунок  1.  Сравнение  амплитудных  кривых  систем  (1)  —  пунктирная  кривая  и  (2)  —  сплошная:  a)  случай  b=0;  б)  случай  b≠0

Поясним  «видимое»  рассогласование  амплитудных  кривых  по  их  интенсивности  —  система  (1)  характеризуется  автоколебаниями  по  углу  увода,  а  амплитуды  автоколебаний  системы  (2)  отнесены  к  поперечной  деформации  пневматика  (если  их  отнести  к  углу  увода  ,  амплитуды  будут  примерно  равные  —  коэффициент  пропорциональности  ). 

Выводы.  Таким  образом,  хотя  при  k=0  структура  области  устойчивости  в  плоскости  параметров  (l,  V)  систем  (1)  и  (2)  не  совпадает,  при  ненулевом  параметре  демпфирования  процессы  автоколебаний  идентичны  как  по  областям  их  возникновения,  так  и  по  интенсивности,  что  указывает  на  «тесную  взаимосвязь»  рассматриваемых  моделей  взаимодействия  упругого  колеса  с  опорной  поверхностью;  учет  пяточного  момента  приводит  к  расширению  области  автоколебаний,  причем  вид  нелинейной  зависимости  пяточного  момента  на  их  интенсивность  практически  не  влияет  (существенны  лишь  линейных  члены  –  линейный  эффект);  уменьшение  коэффициента  сцепления  приводит  к  снижению  интенсивности  автоколебаний  —  нелинейный  эффект.

Список  литературы:

1.Аронович  Г.В.  К  теории  шимми  автомобиля  и  самолета  //  Прикл.  математика  и  механика.  —  1949.  —  13,  №  5.  —  С.  477—488.

2.Вельмагина  Н.А.,  Вербицкий  В.Г.  Анализ  автоколебаний  колесного  модуля  в  прямолинейном  режиме  движения.  //  Механика  твердого  тела.  —  2011.  —  №  41.  С.  100—108.

3.Гоздек  В.С.  О  влиянии  различных  параметров  на  устойчивость  движения  ориентирующихся  колес  самолета//  Тр.  ЦАГИ.  —  1964.  —  Вып.  917.  —  С.  1—30.

4.Гончаренко  В.И.  Каноническое  описание  системы  управления  в  задаче  о  шимми  колес  шасси  самолета.//  Прикл.  механика.  —  2011.  —  47,  №  2,  С.  129—142.

5.Келдыш  М.В.  Шимми  переднего  колеса  трехколесного  шасси.  Избранные  труды.  Механика  /  М.В.  Келдыш.  —  М:  Наука,  1985.  —  С.  491—530.

6.Лобас  Л.Г.  Автоколебания  колеса  на  ориентирующейся  стойке  шасси  с  нелинейным  демпфером  //  Прикл.  математика  и  механика.  —  1981.  —  45,  №  4.  С.  80—87.

7.Марсден  Дж.,  Мак-Кракен  М.  Бифуркация  рождения  цикла  и  ее  приложения.  —  М.:  Мир,  1980.  —  366  с.

8.Неймарк  Ю.И.,  Фуфаев  Н.А.  Динамика  неголономных  систем.  —  М.:  Наука,  1967.  —  C.  520.

9.Плахтиенко  Н.П.,  Шифрин  Б.М.  Поперечные  упруго-фрикционные  вибрации  движущегося  по  взлетно-посадочной  полосе  самолета.//  Прикл.  механика.  —  2001.  —  37,  №  5,  C.  136—143. 

10.Рокар  И.  Неустойчивость  в  механике.  —  М.:  Изд-во  иностр.  Лит.,  1959.  —  288  с.

11.Санников  В.А.  Явление  возбуждения  боковых  колебаний  катящегося  пневматика  при  циклическом  торможении.//Изв.  АНСССР.  МТТ  —  1989.  —  №  3.  —  С.  17—23.

12.Besselink  J.M..  Shimmy  of  aircraft  main  landing  gears.  PhD  thesis,  Delft  University  of  Technology,  2000.  —  P.  201.

13.B.  von  Schlippe  and  R.  Dietrich,  Das  Flattern  eines  bepneuten  Rades,  Bericht  140  der  Lilienthal  Gesellschaft  (1941),  English  translation:  NACA  TM  1365,  1954.  —  P.  125—147.

14.Pacejka  H.B.,  The  wheel  shimmy  phenomenon,  Doctoral  Thesis,  Delft  University  of  Technology,  December  1966.

15.Sharp  R.S.  and  Jones  C.J.,  A  comparison  of  tyre  representations  in  a  simple  wheel  shimmy  problem,  Vehicle  System  Dynamics  9,  1980.  —  P.  45—57.

16.Somieski  G.,  Shimmy  analysis  of  a  simple  aircraft  nose  landing  gear  model  using  different  mathematical  methods.  Aerospace  Science  and  Technology  8,  1997.  —  P.  545—555.

17.Yi.  Mi-Seon,  Bae.  Jae-Sung,  Hwang.  Jae-Hyuk.  Non-linear  shimmy  analysis  of  a  nose  landing  gear  with  friction,  Journal  of  the  Korean  society  for  aeronautical  &  space  sciences,  39,  №  7,  2011.  —  P.  605—611.