Статья опубликована в рамках: III Международной научно-практической конференции «Наука вчера, сегодня, завтра» (Россия, г. Новосибирск, 21 августа 2013 г.)
Наука: Математика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ИСПОЛЬЗОВАНИЕ СХЕМЫ ХАРЛОУ ДЛЯ РАСЧЁТА АЭРОДИНАМИКИ АВТОМОБИЛЯ
Погодин Александр Вячеславович
студент, Нижегородский государственный технический университет им. Р.Е. Алексеева, Н. Новгород
Анучин Илья Евгеньевич
студент, Нижегородский государственный технический университет им. Р.Е. Алексеева, Н. Новгород
Катаева Лилия Юрьевна
д-р физ.-мат. наук доцент, Нижегородский государственный технический университет им. Р.Е. Алексеева, Н. Новгород
Масленников Дмитрий Александрович
канд. физ.-мат. наук Нижегородский государственный технический университет им. Р.Е. Алексеева, Н. Новгород
E-mail: dmitrymaslenikov@rambler.ru
Исследования выполнены при финансовой поддержке Министерства образования и науки РФ в рамках проекта по договору № 02.G25.31.0006 от 12.02.2013 г. (постановление Правительства Российской Федерации от 9 апреля 2010 года № 218).
Моделирование аэродинамики обуславливает серьёзные ограничения на соотношение шагов по времени и по пространству, связанное со скоростью звука, поэтому важно использовать существующие возможности по минимизации времени вычислений. Другой особенностью, которую необходимо учитывать при выборе метода моделирования обтекания автомобиля является необходимость учитывать произвольную форму автомобиля, что, при использовании прямоугольной сетки, приводит к возникновению большого количества угловых точек.
Проведено численное исследование аэродинамики автомобиля в двумерной и трехмерной постановке. В математической модели использованы нестационарные уравнения Навье-Стокса и криволинейные, адаптированные к форме объекта расчетные сетки.
В работе [1] авторы моделируют аэродинамику автомобиля, как в двумерной, так и в трехмерной постановке. Используются криволинейные, адаптированные к форме обтекаемого объекта расчетные сетки
В отличие от метода Патанкара [3], метод Харлоу [5] обладает большей устойчивостью, хотя и менее точен.
Для моделирования обтекания автомобиля используется математическая постановка в следующем виде [2]:
![]() , (1)
, (1)
· уравнение сохранения количества движения проекций скоростей ![]() и
и ![]()
 , (2)
, (2)
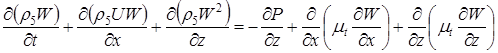 . (3)
. (3)
![]() (4)
(4)
Предполагалось, что автомобиль движется с постоянной скоростью Ue=28.8 м/с относительно поверхности земли, ветер отсутствует. Численные расчёты производятся в системе отсчёта, связанной с автомобилей, в этой системе отсчёта дорожное полотно (нижняя граница расчётной области) и воздух, на достаточном удалении, движутся со скоростью Ue, тогда как сам автомобиль покоится. Для моделирования движения используются граничные условия в следующем виде:
![]() , (5)
, (5)
![]() , (6)
, (6)
![]() , (7)
, (7)
![]() (8)
(8)
![]() (9)
(9)
где: G — граница автомобиля.
Как можно видеть (5)—(9) не содержат выражений для вычисления давления на границах, что создаёт сложности при его вычислении. Чтобы их обойти, целесообразно использовать разнесённый шаблон, структура которого показана на рис. 1. Вся расчётная область разбивается на прямоугольные ячейки равного размера. В центре каждой ячейки определяется давление и плотность, а на гранях величина скорости, в направлении им перпендикулярном. Моделирования геометрии обтекаемого объекта, определяется при помощи множества ячеек, центры которых принадлежат ему.
Для реализации границы, связанной с автомобилем, в каждой ячейке расчётной сетки определяется Bi,j, равное нулю, если (i,j) является частью обтекаемого тела, и единицe иначе. Предполагается, что соотношение (9) выполняется на каждой грани между свободной ячейкой и ячейкой, принадлежащей обтекаемому объекту.

Рисунок 1. Структура разнесённой сетки
Благодаря использованию разнесённого шаблона, была снята необходимость вычисления давления на границах. Хотя, в задачах аэродинамики необходимо учитывать давление на поверхности тела, оно считается постоянным внутри одной ячейки.
Для вычисления общей величины сила, которую поток воздуха, оказывает на автомобиль, вычислялась векторная сумма сил, действующая на грани, составляющие границу обтекаемого тела. Сила, действующая на одну грань, определялась как произведение давления в примыкающей к ней ячейке, не принадлежащей телу, умноженную на площадь грани. Направление этой силы соответствовало нормали к грани, направленной внутрь автомобиля. Схема вычисления силы, действующей на автомобиль, показана на рис. 2.

Рисунок 2. Схема вычисления силы, действующей на автомобиль
Учитывая рассматриваемую систему уравнений и граничные условия (1—9), численная схема может быть записана в виде (10). При необходимости вычисления значений на половинных узлах, используется среднеарифметическое известных значений на соседних точках. Уравнение (10) можно интерпретировать как изменение некой сохраняющейся физической величины ![]() за счёт потоков через границы ячейки и источникового слагаемого.
за счёт потоков через границы ячейки и источникового слагаемого.
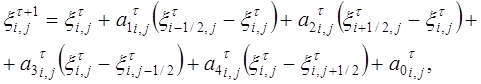 (10)
(10)
где: ![]() , (k=0…4) — некоторые коэффициенты,
, (k=0…4) — некоторые коэффициенты,
![]() — обобщённая переменная, (значение искомой величины),
— обобщённая переменная, (значение искомой величины),
![]() — её значение на дискретной сетке,
— её значение на дискретной сетке,
i,j — пространственные дискретные координаты,
![]() — номер шага по времени.
— номер шага по времени.
В данной работе показаны особенности моделирования обтекания автомобиля. Хотя существуют более мощные программные комплексы, предназначенные для расчёта гидродинамики, такие как Star CCM+ [4], XFlow 2012 [6], написание программ на таких языках как Matlab, C++, Java позволяет более детально и гибко прорабатывать алгоритм и анализировать влияние отдельных его элементов на результат.
Список литературы:
1.Кульпина И.Э., Перминов С.М., Писковский В.О., Соколов А.Г. Численное моделирование процесса обтекания автомобиля // Матем. моделирование, 6:1 (1994), — с. 54—68.
2.Масленников Д.А. Влияние холмов на динамику лесного пожара / Д.А. Масленников, Л.Ю. Катаева, Н.В. Галина // Успехи современного естествознания: материалы конференции / Пенза — 2012. — № 6 — С. 189—189.
3.Романов A.B., Катаева Л.Ю. Метод Патанкара и возможности его оптимизации// Наука и техника транспорта, № 3, 2008. М.:РГОТУПС
4. Саровский инженерный центр — [Электронный ресурс] — Режим доступа. — URL: http://www.saec.ru/starccmplus/ (дата обращения 20.08.2013).
5.Численные методы в задачах физики быстропротекающих процессов: учебник для втузов / А.В. Бабкин, В.И. Колпаков, В.Н. Охитин, В.В. Селиванов. — 2-е изд., испр. М.: Изд-во МГТУ им. Н.Э. Баумана, 2006. — 520 с.
6.XFlow Next generation CFD. — [Электронный ресурс] — Режим доступа. — URL: http://www.xflow-cfd.com/ (дата обращения 20.08.2013).
дипломов


Оставить комментарий