Статья опубликована в рамках: XIV Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 10 октября 2012 г.)
Наука: Технические науки
Секция: Инженерная графика, САПР, CAD, CAE
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ГЕОМЕТРИЧЕСКОЕ МОДЕЛИРОВАНИЕ ОБОЛОЧЕК МНОГОСЛОЙНОЙ СТРУКТУРЫ НА ОСНОВЕ ПРИМЕНЕНИЯ РАЦИОНАЛЬНЫХ ФУНКЦИЙ
Аюшеев Тумэн Владимирович
д-р техн. наук, доцент Восточно-Сибирского государственного университета технологий и управления (ВСГУТУ), г. Улан-Удэ
E-mail: atv_a@mail.ru
Прудова Людмила Юрьевна
канд. техн. наук, ВСГУТУ, г. Улан-Удэ
Бубеев Иннокентий Трофимович
канд. техн. наук, ВСГУТУ, г. Улан-Удэ
GEOMETRICAL MODELING OF THE INTEGUMENTS OF MULTI-LAYER STRACTURE ON THE BASIS OF APPLYING RATIONAL FUNCTIONS
Tumen V. Ayusheyev
Doctor of Technical Sciences, Associate Professor of East-Siberia state university of technologies and management, Ulan-Ude
Lyudmila Yu. Prudova
Candidate of Technical Science, ESSUTM, Ulan-Ude
Inokenti Bubeyev
Candidate of Technical Science, ESSUTM, Ulan-Ude
Аннотация
В статье рассматривается способ математического описания порции трехмерного тела многослойной структуры для деталей сложной форма, изготавливаемых намоткой из волокнистых композиционных материалов, на основе применения рациональных кубических параметрических функций
ABSTRACT
There has been studied the method of mathematical description of the portion of a 3D body with the multi-layer structure for details of a complex form that are manufactured from fiber composite materials on the basis of applying rational cubic parametric functions.
Ключевые слова: трехмерное тело; математическое описание; рациональные кубические параметрические функции.
Keywords: 3D body; mathematical description; rational cubic parametric functions.
При моделировании оболочечных конструкций сложной формы, изготавливаемых намоткой из волокнистых композиционных материалов, возникают важные геометрические задачи построения сеток граничных и промежуточных поверхностей для расчета параметров процесса намотки твердых деформируемых тел многослойной структуры.
Существуют различные методы математического описания таких тел на основе поверхностных и объемных твердотельных моделей. Анализ существующих решений показывает, что из-за начальных несовершенств формы технологической поверхности оправки использование поверхностных моделей при моделировании процесса намотки многослойных оболочек затрудняет коррекцию формы оправки. Корректировка формы оправки сопровождается переработкой больших объемов информации, из-за требований перезадания исходного точечного каркаса и моделирования поверхности по новому каркасу для всех слоев оболочки наматывания. Для более эффективного представления массивов входных и выходных данных различных этапов моделирования необходимо перейти от дискретных значений к аналитическому описанию, что избавляет от необходимости переработки и хранения больших объемов информации и повышает качество интерполирования. Наиболее целесообразным решением этой проблемы представляется моделирование тела намотки на основе объемного трехмерного моделирования, что требует применения современных технологий, среди которых наиболее перспективным является способ граничного представления сплошных тел.
В работах [1, 2] рассматриваются методы получения уравнения порции тела на его основе, в частности, с использованием линейной обобщенной интерполяции и обобщенной интерполяции Эрмита. В указанных методах в качестве граничных кривых порции тела используются параметрические кубические кривые. В данной работе рассматривается метод описания порции тела на основе использования рациональных кубических кривых, который отличается большей общностью. Как известно, конические сечения и параметрические кубические кривые являются частным случаем рациональной кубической кривой [3].
Сегмент рациональной кубической кривой определяется формулой [3]:
![]()
![]() (1)
(1)
где ![]() — константы, или веса,
— константы, или веса, ![]() — опорные точки, u — параметр кривой.
— опорные точки, u — параметр кривой.
Можно выразить этот сегмент кривой в виде
![]() (2)
(2)
через его концевые точки, концевые касательные и функции сопряжения. Напомним, что
![]()
![]()
![]()
![]()
![]()
![]() (3)
(3)
![]()
![]()
где ![]() означает знаменатель в выражении (1).
означает знаменатель в выражении (1).
Используя формулу (2) можно описать граничные кривые порции тела намотки (рис. 1).
![]()
![]()
![]()
![]()

Рисунок 1. Порция тела намотки
Тогда уравнение порции тела намотки можно записать в виде:
![]()
![]() (4)
(4)
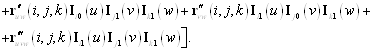
где функции смешения ![]() определены формулой (3).
определены формулой (3).
Уравнение порции тела намотки (4) удобно представить в матричной форме:
![]() (5)
(5)
где ![]() — матрица-строка,
— матрица-строка,
![]() — матрица-столбец,
— матрица-столбец,


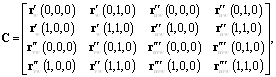

Порция тела (5) полностью определена через векторы r, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() в ее восьми углах, т.е. через компоненты матриц A, B, C и D.
в ее восьми углах, т.е. через компоненты матриц A, B, C и D.
В данном методе расчет параметров порции тела намотки производится аналогично методике построения тела составной формы из однородных материалов. Положения углов порций задаются с самого начала, а векторы производных в углах определяются в результате построения сетки сплайновых кривых. Их можно определить таким образом, что вся составная поверхность тела каждого слоя будет обладать непрерывностью кривизны в том смысле, что непрерывно поперек всех границ тела.
Программная реализация разработанного метода показала достаточно хорошую вычислительную устойчивость и гибкость управления, как внешней формой, так и внутренней структурой с учетом заданных дифференциальных характеристик порции тела намотки. В отличие от известных методов описания порции тела, использующих параметрические кубические кривые, дополнительную гибкость в управлении внешней формой и внутренней структурой тела без изменения векторов положения и векторов производных придают весовые коэффициенты (1). Это дает возможность значительно сократить объем вычислений, связанный с дополнительным перезаданием исходного каркаса тела намотки с целью получения заданных характеристик изделия.
Список литературы:
1. Аюшеев Т.В. Метод построения модели сплошного тела с применением обобщенной линейной интерполяции // Автоматизация и современные технологии. 2005. № 6. С. 35—40.
2. Аюшеев Т.В. Метод построения сплошных тел с применением обобщенной интерполяции Эрмита // Информационные технологии. 2005. № 6. С. 27—32.
3. Фокс А., Пратт М. Вычислительная геометрия. Пер. с англ. М.: Мир, 1982. — 304 с.
дипломов


Оставить комментарий