Статья опубликована в рамках: XL Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 19 ноября 2014 г.)
Наука: Технические науки
Секция: Машиностроение и машиноведение
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
РАЗРАБОТКА МАТЕМАТИЧЕСКОЙ МОДЕЛИ ДВИЖЕНИЯ УЗЛА С ПОДАТЛИВЫМ КРЕПЛЕНИЕМ ПРИ АВТОМАТИЗИРОВАННОЙ СБОРКЕ ДЕТАЛЕЙ
Пантелеев Евгений Юрьевич
канд. техн. наук, доцент, Ковровская государственная технологическая академия, РФ, г. Ковров
E -mail: pant33@mail.ru
Кузнецова Светлана Владимировна
канд. техн. наук, доцент Ковровская государственная технологическая академия, РФ, г. Ковров
E-mail:
DEVELOPMENT OF A MATHEMATICAL MODEL OF THE MOTION NODE MALLEABLE FIXING AUTOMATED ASSEMBLY PARTS
Evgeny Panteleev
cand. tehn. sciences, Kovrovskaya State Technological Academy, Russia, Kovrov
Svetlana Kuznetsova
cand. tehn. sciences, Kovrovskaya State Technological Academy, Russia, Kovrov
АННОТАЦИЯ
Для выявления возможности осуществления автоматизированного совмещения собираемых деталей исследуется процесс осевого и углового совмещения осей соединяемых деталей. Приводятся дифференциальные уравнения, описывающие движение системы патрон-платформа с податливым креплением в процессе пассивной адаптации при сборке деталей. Полученные выражения определяют условия собираемости соединяемых деталей в динамике.
ABSTRACT
To identify the feasibility of the automated alignment of collected parts explores the process of axial and angular alignment of the axes of the parts. Given the differential equations describing the motion of the cartridge-mounting platform with pliable during passive adaptation of the assembly parts. The obtained expressions define the conditions of collection of the parts in the dynamics.
Ключевые слова: автоматизированное совмещение; условия собираемости
Keywords: automated alignment; terms of collection
Величина относительного смещения и угол перекоса осей соединяемых деталей в сборочном оборудовании может достигать значений, превосходящих в несколько раз допустимые условия собираемости [1]. Практически при таких смещениях без адаптации сборку осуществить невозможно. На основании способа пассивной адаптации [2] предлагается обеспечить податливость одной из собираемых деталей при помощи подающего устройства.
Конструктивная реализация такого устройства может быть представлена расчетной схемой, изображенной на рис. 1. Исследуем процесс автоматизированного совмещения собираемых деталей, который будет происходить в 4 этапа.
Первый этап — попадание конца соединяемой детали в зону отверстия на собираемом узле. Попадание обеспечивается за счет смещений конца соединяемой детали (в пределах зазора в сопряжении патрона со шпинделем завинчивающего устройства) и узла (имеющего осевую и угловую податливость крепления подвеса к подающему устройству) при медленном опускании вращающейся соединяемой детали после ее касания поверхности узла. При этом, за счет силового взаимодействия, конец соединяемой детали, из-за изменения угла с податливым узлом, будет двигаться по его поверхности по траектории близкой к спирали Архимеда, что позволит обеспечить попадание в зону отверстия, а следовательно и осевое совмещение осей.
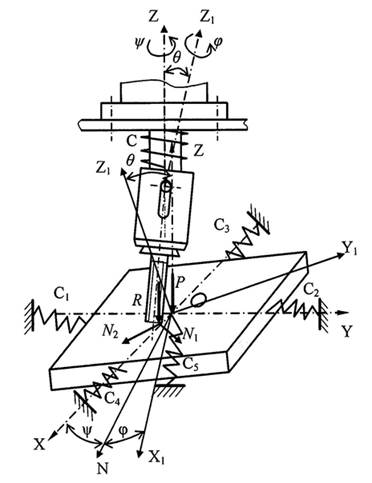
Рисунок 1. Силовое взаимодействие собираемых деталей в процессе сборки
Второй этап — в момент попадания конца детали в зону отверстия, при определенных соотношениях параметров, конец детали может остаться в зоне отверстия либо выйти из него, начав новое скольжение по его поверхности. В работе [2] доказаны условия невыхода конца детали из отверстия.
Третий этап — скольжение конца соединяемой детали в углублении, образованном фаской отверстия, и движение узла с податливым креплением под действием силы взаимодействия, при которых возможно обеспечить угловое совмещение осей сопрягаемых поверхностей соединяемых деталей.
Для выявления возможного углового совмещения осей составим дифференциальные уравнения движения системы. Система имеет 6 степеней свободы. В качестве обобщенных координат возьмем:
1. углы Эйлера:
j — угол собственного вращения вокруг оси Z1;
y — угол нутации, т.е. движение податливого крепления подающего устройства вокруг оси Z1;
q — угол наклона податливого подающего устройства вокруг линии узлов;
2. координаты смещения центра масс подающего устройства: C,U,Z.
Для исследования процесса осевого и углового совмещения осей соединяемых деталей достаточно 4х степеней свободы: j, y, q, Z.
Для составления дифференциальных уравнений движения системы, состоящей из соединяемой детали и податливого узла, воспользуемся уравнением Лагранжа 2-го рода.
Для упрощения процесса определения обобщенных сил распишем силы и моменты, действующие в процессе взаимодействия.
Предварительно введем следующие обозначения:
с — жесткость пружин 1, 2, 3, 4;
с 5 — жесткость пружины 5;
с п — жесткость пружины патрона;
k — угловая жесткость пружин 1, 2, 3, 4;
k 5 — угловая жесткость пружины 5;
k п — угловая жесткость пружины патрона;
b — длина пружин 1, 2, 3, 4;
b 5 — длина пружины 5;
х , y, z — перемещение платформы вдоль осей X, Y, Z;
l — половина длины платформы вдоль оси X или Y;
r — расстояние от центра платформы до точки действия силы R;
a п — величина предварительного поджатия пружины патрона;
G п — вес патрона;
q 1 — величина изгиба пружины патрона за счет зазора в направляющей;
D — зазор между внутренним отверстием патрона и диаметром шпинделя;
d — длина взаимодействия шпинделя и патрона;
Пружина 1.
а. 
— сила, действующая на пружину при смещении платформы по оси U1, направленная в противоположную сторону от U1 ;
б. 
— изгибающий момент, создаваемый пружиной 1 при повороте платформы вокруг оси Z1 под действием силы N1, вектор момента направлен по оси Z1,
где: 
;
в. 
— изгибающий момент, создаваемый пружиной 1 при перемещении по оси X1 под действием силы N2, вектор момента направлен по оси Z1,
г. 
— изгибающий момент, создаваемый пружиной 1 при повороте платформы вокруг линии узлов Nузл под действием силы R, вектор момента направлен по оси Х1;
д. 
— изгибающий момент, создаваемый пружиной 1 при перемещении платформы вдоль оси Z1 под действием силы Р, вектор момента направлен по оси Х1;
Пружина 2.
а. 
— сила, действующая на пружину при смещении платформы по оси U1, направлена в противоположную сторону от U1 ;
б. 
— изгибающий момент, создаваемый пружиной 2 при повороте платформы вокруг оси Z1 под действием силы N1, вектор момента направлен по оси Z1;
в. 
= 
— изгибающий момент, создаваемый пружиной 2 при перемещении по оси X1 под действием силы N2, вектор момента направлен в противоположную сторону от Z1;
г. 
— изгибающий момент, создаваемый пружиной 2 при повороте платформы вокруг линии узлов Nузл под действием силы R, вектор момента направлен по оси Х1;
д. 
— изгибающий момент, создаваемый пружиной 2 при перемещении платформы вдоль оси Z1 под действием силы Р, вектор момента направлен в противоположную сторону от X1;
Пружина 3.
а. 
— сила, действующая на пружину при смещении платформы по оси X1, направлена в противоположную сторону от X1 ;
б. 
— изгибающий момент, создаваемый пружиной 3 при повороте платформы вокруг оси Z1 под действием силы N1, вектор момента направлен по оси Z1;
в. 
— изгибающий момент, создаваемый пружиной 3 при перемещении по оси X1 под действием силы N2, вектор момента направлен в противоположную сторону от Z1;
г. 
— изгибающий момент, создаваемый пружиной 3 при повороте платформы вокруг линии узлов Nузл под действием силы R, вектор момента направлен по оси Y1;
д. 
— изгибающий момент, создаваемый пружиной 3 при перемещении платформы вдоль оси Z1 под действием силы Р, вектор момента направлен по оси Y1;
Пружина 4.
а. 
— сила, действующая на пружину при смещении платформы по оси X1, направлена в противоположную сторону от X1 ;
б. 
— изгибающий момент, создаваемый пружиной 4 при повороте платформы вокруг оси Z1 под действием силы N1, вектор момента направлен по оси Z1;
в. 
— изгибающий момент, создаваемый пружиной 4 при перемещении по оси X1 под действием силы N2, вектор момента направлен по оси Z1;
г. 
— изгибающий момент, создаваемый пружиной 4 при повороте платформы вокруг линии узлов Nузл под действием силы R, вектор момента направлен по оси Y1;
д. 
— изгибающий момент, создаваемый пружиной 4 при перемещении платформы вдоль оси Z1 под действием силы Р, вектор момента направлен по оси Y1;
Пружина 5.
а. 
— сила, действующая на пружину при смещении платформы по оси Z1, направлена по оси Z1 ;
б. 
— изгибающий момент, создаваемый пружиной 5 при перемещении по оси X1 под действием силы N2, вектор момента направлен в противоположную сторону от Y1;
в. 
— изгибающий момент, создаваемый пружиной 5 при перемещении по оси Y1 под действием силы N2, вектор момента направлен по оси X1;
г. 
— изгибающий момент, создаваемый пружиной 5 под действием силы R при перемещении платформы по оси Y1, вектор момента направлен в противоположную сторону от X1;
д. 
— изгибающий момент, создаваемый пружиной 5 под действием силы R при перемещении платформы по оси X1, вектор момента направлен в противоположную сторону от Y1;
Моменты закручивания всех пружин не учитывались, поскольку пружины закреплены таким образом, что могут поворачиваться вокруг собственных осей.
Кинетическая энергия механической системы патрон — податливая платформа, оси которой являются главными осями инерции, запишется:
,
где: I1=I2 — моменты инерции платформы относительно О1X1 и О1Y1, 
;
— момент инерции платформы относительно оси О1Z1;
w 1, w2, w3 — соответственно проекции вектора абсолютной угловой скорости на оси X1, Y1, Z1;
, 
, 
— соответственно проекции вектора абсолютной скорости на оси X1, Y1, Z1;
m — масса платформы.
Используя кинематические уравнения Эйлера, с учетом малости угла нутации q, проекции w1, w2, w3 на неподвижные оси координат, запишутся:
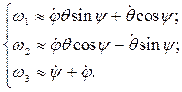
Отсюда
Кинетическая энергия системы запишется:
Окончательно дифференциальные уравнения системы имеют вид:
Если во втором уравнении системы пренебречь первым слагаемым, ввиду малости угла q и сомножителей 
и 
, которые являются величинами второго порядка малости, левые части первого и второго уравнения будут одинаковы. Кроме того, при установившемся процессе вращения 
активные моменты будут равны противодействующим
и правые части этих уравнений будут равны нулю.
Следовательно, прецессия платформы будет происходить с угловой скоростью 
. Это указывает на то, что при скольжении конца цилиндрической детали во впадине, образованной фаской отверстия или заходными кромками резьбового отверстия на поверхности узла, прецессия платформы на податливом креплении будет происходить с угловой скоростью w в направлении противоположном вращению шпинделя и за счет наклона платформы будет происходить совмещение осей сопрягаемых деталей.
В третьем уравнении слагаемое r×sinq =z, значение z можно определить, решая четвертое уравнение. Решение третьего уравнения даст закон изменения угла нутации, т.е. углового совмещения осей соединяемых деталей. Решение этого уравнения можно получить, используя численные методы, с помощью ЭВМ.
При условии, если полученное q будет меньше предельно допустимого значения перекоса, определяемого условиями собираемости, автоматизированное совмещение обеспечено. Полученное выражение q, с учетом (1), даст условия собираемости соединяемых деталей в динамике.
Таким образом, получены дифференциальные уравнения, описывающие движение системы патрон — платформа с податливым креплением в процессе пассивной адаптации при сборке деталей, сопрягаемых по цилиндрическим поверхностям с зазором или по резьбовым поверхностям. Решение уравнений позволяет определить возможность автоматизированного углового совмещения осей при сборке. Полученные выражения определяют условия собираемости соединяемых деталей в динамике.
Список литературы:
1.Гусев А.А. Адаптивные устройства сборочных машин. М.: Энергия, 1971.
2.Житников Ю.З. Автоматизация сборки изделий с резьбовыми соединениями: Учебн. пособие. Ковров: КГТА, 1996. — 132 с.
дипломов
Оставить комментарий