К  ВОПРОСУ  ОБ  ОПРЕДЕЛЕНИИ  ПРОДОЛЬНЫХ  РАЗМЕРОВ  ГИДРОДИНАМИЧЕСКИХ  КАВИТАЦИОННЫХ  УСТРОЙСТВ

Прохасько  Любовь  Савельевна

канд.  техн.  наук,  доцент  ФГБОУ  ВПО  «Южно-Уральский  государственный  университет»  (национальный  исследовательский  университет),  г.  Челябинск

E-mail:  prokhaskols@mail.ru

Ярмаркин  Дмитрий  Александрович

студент  ФГБОУ  ВПО  «Южно-Уральский  государственный  университет»  (национальный  исследовательский  университет),  г.  Челябинск

E-mail: 

TO  THE  QUESTION  OF  DETERMINATION  OF  THE  LONGITUDINAL  SIZES  OF  HYDRODYNAMIC  CAVITATIONAL  DEVICES

Lubov  Prokhasko

candidate  of  engineering  sciences,  associate  professor  of  South  Ural  State  University  (national  research  University),  Chelyabinsk

Dmitry  Yarmarkin

student  of  South  Ural  State  University  (national  research  University),  Chelyabinsk

АННОТАЦИЯ

Рассмотрены  некоторые  аспекты  математической  модели  рабочего  процесса  гидродинамического  кавитационного  устройства  со  скачком  давления.  Уравнения,  позволяющие  определить  протяженность  критического  участка  с  бурным  двухфазным  течением,  переходящим  в  спокойное  дозвуковое  в  скачке  давления.  Длина  критического  участка  определяет  протяженность  рабочей  камеры  кавитационного  устройства. 

ABSTRACT

Some  aspects  of  mathematical  model  of  working  process  of  the  hydrodynamic  cavitational  device  with  pressure  jump  are  considered.  The  equations,  allowing  to  determine  the  extent  of  a  critical  site  with  the  rapid  two-phase  current  passing  to  quiet  subsonic  in  pressure  jump.  Length  of  a  critical  site  determines  the  extent  of  the  working  camera  of  the  cavitational  device

Ключевые  слова:  кавитация;  сверхзвуковое  течение;  дозвуковое  течение;  скачок  давления;  двухфазная  среда.

Keywords:  cavitation;  supersonic  stream;  subsonic  stream;  pressure  jump;  two-phase  environment.

Известны  гидродинамические  кавитационные  устройства,  рабочий  процесс  которых  основан  на  создании  сверхзвукового  течения  двухфазного  потока,  переходящего  в  дозвуковой  режим  в  скачке  давления  [1—9].  Задача  расчета  сводится  к  определению  размеров  устройства,  отвечающим  минимальным  потерям  давления  и,  следовательно,  минимальному  энергопотреблению.  При  этом  важны  как  поперечные,  так  и  продольные  размеры,  ибо  выбор  поперечных  размеров  обусловлен  разгоном  двухфазного  потока  до  критических  скоростей  и  формированием  сверхзвукового  двухфазного  потока.  Выбор  продольных  размеров  предопределен  положением  скачка  давления  в  проточной  части  устройства.  Завышение  этих  размеров  приводит  к  увеличению  материалоемкости  и  дополнительным  затратам  энергии,  занижение  —  к  неэффективной  работе  устройства. 

В  общем  случае  скорости  движения  жидкости  и  пара  (газа)  в  гидродинамическом  кавитационном  устройстве  различны.  Вследствие  этого  данные  по  расходу  среды,  геометрии  канала  и  физическим  свойствам  жидкости  и  газа  (пара)  еще  не  дают  достаточно  полного  представления  о  гидродинамике  потока.  Поэтому  для  характеристики  двухфазного  потока  необходимо  вводить  величины,  учитывающие  особенности  движения  отдельных  фаз. 

Параметром,  характеризующим  состояние  потока,  является  число  Маха.  При  критическом  состоянии  потока  число  Маха  М=1,  при  сверхзвуковом  течении  ,  при  дозвуковом  течении  <1.  Критическое  состояние  потока  соответствует  минимуму  удельной  энергии  сечения.  Давление,  соответствующее  минимуму  удельной  энергии  сечения,  называется  критическим  Р_к.  В  зависимости  от  соотношения  действительного  Р  и  критического  Р_к  давлений  в  газожидкостном  потоке  его  энергетическое  состояние  может  быть  бурным  сверхзвуковым  Р<Р_к,  спокойным  дозвуковым  Р>Р_к  или  критическим  Р=Р_к.  Переход  потока  из  одного  состояния  в  другое  возможен  только  в  скачке  давления.

Организация  течения  двухфазного  потока  со  скачком  давления  предполагает  значительную  протяженность  рабочей  камеры.  Математическое  описание  рабочего  процесса  гидродинамического  кавитационного  устройства  целесообразно  выполнить  на  основе  гомогенной  равновесной  модели,  которая  предполагает  следующие  допущения:  жидкая  и  парогазоваяфазы  находятся  в  тепловом  и  механическом  равновесии  (температуры  и  скорости  фаз  равны);  фазы  равномерно  распределены  одна  в  другой;  двухфазная  среда  изотропна.  Этого  можно  достичь  применением  многоструйного  сопла,  которое  формирует  несколько  высокоскоростных  струй,  в  пограничных  слоях  которых  в  центрах  низкого  давления  турбулентных  вихрей  возникает  кавитация.  Таким  образом,  многоструйное  сопло  обеспечивает  устойчивый  процесс  кавитационных  явлений,  а  также  равномерное  формирование  компонентов  двухфазного  потока  по  живому  сечению.  В  этих  условиях  коэффициент  скольжения  близок  к  единице,  а  двухфазное  течение  может  рассматриваться  как  течение  квазиоднородной  изотермической  (гомогенной)  среды.

Критическое  давление  потока  можно  определить  по  уравнению  [5,  10]:

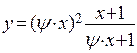,  (1)

где:  x  и  у  —  безразмерные  координаты:

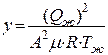  .  (2)

Здесь  Р  —  давление  в  сечении  потока;

m  —  отношение  массовых  долей  газа  (пара)  и  жидкости;

R  —  газовая  постоянная;

T_ж  —  температура  жидкой  фазы;

r_ж  —  плотность  жидкой  фазы;

Q_ж  —  объемный  расход  жидкой  фазы;

А  —  площадь  сечения  потока.

Для  определения  длины  рабочей  камеры  кавитационного  устройства  необходимо  рассчитать  критическую  длину  l_к  с  бурным  двухфазным  потоком,  в  концевом  сечении  участка  которой  достигается  критическое  состояние  потока  (давление  Р=Р_к).  Для  этого  можно  использовать  уравнение  [3,  8],  интегрирование  которого  позволит  рассчитать  критическую  длину  и,  тем  самым,  определить  длину  рабочей  камеры  [3,  8]:

  (3)

где:  А  —  площадь  живого  сечения  потока;

R  —  гидравлический  радиус;

l  —  коэффициент  гидравлического  трения;

l  —  протяженность  участка  с  бурным  двухфазным  потоком;

М  —  число  Маха.

Список  литературы:

1.Кондратьева  А.В.  Новые  технологии  обработки  молочной  продукции  (на  примере  молока  коровьего  питьевого)  /  Кондратьева  А.В.,  Ярмаркин  Д.А.,  Прохасько  Л.С.,  Асенова  Б.К.,  Залилов  Р.В.  //  Молодой  ученый.  —  2013.  —  №  10.  —  С.  146—149.

2.Лиходумова  М.А.  Инновационные  технологии  водоподготовки  для  производства  слабо–  и  безалкогольной  продукции  /  Лиходумова  М.А.,  Ярмаркин  Д.А.,  Прохасько  Л.С.,  Асенова  Б.К.,  Залилов  Р.В.  //  Молодой  ученый.  —  2013.  —  №  10.  —  С.  159—161.

3.Патент  РФ  №  99105906/12,  10.11.2000.  Спиридонов  Е.К.,  Прохасько  Л.С.,  Боковиков  В.С.,  Валиев  А.Х.  Смеситель  кавитационного  типа  //  Патент  России  №  2158627.  1999.  Бюл.  №  31.

4.Патент  РФ.  Прохасько  Л.С.,  Ребезов  М.Б.,  Зинина  О.В.,  Залилов  Р.В.,  Мазаев  А.Н,  Асенова  Б.К.,  Ярмаркин  Д.А.  Смеситель  кавитационного  типа  для  жидких  пищевых  сред  //  Патент  России  №  2013117605.  2013.  Решение  о  выдаче  патента  11.09.2013  (патент  на  публикации).

5.Прохасько  Л.С.  Гидродинамика  и  расчет  кавитационных  смесителей  непрерывного  действия:  Автореф.  дис.  канд.  техн.  наук  Пермь,  2000.  —  20  с.

6.Прохасько  Л.С.  Применение  гидродинамических  кавитационных  устройств  для  дезинтеграции  пищевых  сред  /  Л.С.  Прохасько,  М.Б.  Ребезов,  Б.К.  Асенова,  О.В.  Зинина,  Р.В.  Залилов,  Д.А.  Ярмаркин  //  Сборник  научных  трудов  Sworld  по  материалам  международной  научно-практической  конференции.  —  2013.  —  Т.  7.  —  №  2.  —  С.  62—67.

7.Прохасько  Л.С.  Гидродинамическая  кавитационная  технология  обработки  пищевых  сред  /  Л.С.  Прохасько,  В.А.  Евдокимов  //  Наука.  Образование.  Молодежь:  мат.  научн.-практ.  конф.,  посв.  55-летию  АТУ    Алматы,  2012.  —  С.  256—257.

8.Прохасько  Л.С.  Расчет  кавитационных  устройств  для  обработки  жидких  пищевых  сред  /  Л.С.  Прохасько,  Р.В.  Залилов,  Я.М.  Ребезов  //  Техника  и  технология  пищевых  производств:  мат.  IХ  междунар.  науч.-технич.  конф.  Могилев,  2013.  —  С.  260.

9.Прохасько  Л.С.  Применение  гидродинамических  кавитационных  устройств  для  процессов  водоочистки  /  Л.С.  Прохасько  //  Международная  научно-практическая  конференция  «Чистая  вода  —  2009»:  сб.  науч.  тр.  Кемерово,  2009.  —  С.  460—464. 

10.Спиридонов  Е.К.  Теоретические  основы  расчета  и  проектирования  жидкостногазовых  струйных  насосов:  Автореф.  дис.  доктора  техн.  наук.  М.,  1996.  —  30  с.