Статья опубликована в рамках: XXVIII Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 27 ноября 2013 г.)
Наука: Технические науки
Секция: Инженерная графика, САПР, CAD, CAE
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ПРИМЕНЕНИЕ ГЕОМЕТРИЧЕСКОГО АППАРАТА СУПЕРПОЗИЦИЙ В ДИСКРЕТНОМ МОДЕЛИРОВАНИИ ОБЪЕКТОВ СТРОИТЕЛЬСТВА И МАШИНОСТРОЕНИЯ
Воронцов Олег Викторович
канд. техн. наук, доцент ПолтНТУ им. Юрия Кондратюка, Украина, г. Полтава
E-mail: uaag.poltava2012@gmail.com
Усенко Валерий Григорьевич
канд. техн. наук, доцент ПолтНТУ им. Юрия Кондратюка, Украина, г. Полтава
GEOMETRICAL SUPERPOSITION SET APPLICATION IN DISCRETE GEOMETRICAL OBJECT DESIGN IN CIVIL ENGINEERING AND MACHINE BUILDING
Oleg Vorontsov
candidate of Technical Sciences, Associate Professor of Poltava National Technical University of the name of Yuriy Kondratyk, Ukraine Poltava
Valery Usenko
candidate of Technical Sciences, Associate Professor of Poltava National Technical University of the name of Yuriy Kondratyk, Ukraine Poltava
АННОТАЦИЯ
В статье рассмотрены задачи, выполнены обобщения и обоснована целесообразность системных исследований геометрических свойств аппарата суперпозиций и определения на их основе главных аспектов нового направления дискретного формирования геометрических образов объектов машиностроения и строительства.
ABSTRACT
The tasks of discrete geometric modeling have been considered and generalizations made in this article. The expediency of geometrical superposition set systematic studying has been reasoned. On its basis the new direction within main aspects of discrete geometric models for construction and machine building objects formation has been determined.
Ключевые слова: прикладная геометрия; дискретное геометрическое моделирование; метод конечных разностей; статико-геометрический метод; математический аппарат числовых последовательностей; геометрический аппарат суперпозиций.
Keywords: applied geometry; discrete geometric modeling; method of finite differences; statistic-and- geometric method; the body of mathematics for numerical sequences; geometrical superposition set.
Постановка проблемы. Развитие производства и усовершенствование технологических процессов ставят перед наукой новые задачи по созданию адекватных моделей объектов процессов и явлений для их эффективного анализа, расчета, оптимизации и прогнозирования. Современное состояние проектирования криволинейных объектов машиностроения и строительства нуждается в учете как можно большего количества выходных данных и требований для обеспечения соответствующей точности модели. При геометрическом моделировании выходными данными, как правило, выступают геометрические характеристики и условия, чаще всего представленные в числовой форме (координаты или значения параметров), массивы которых могут быть достаточно большими. В этих условиях методы глобального непрерывного моделирования, когда отыскивается единственное решение, оказываются неэффективными, потому что обычно требуют использования достаточно сложных математических алгоритмов и не могут обеспечить необходимую адекватность модели. Отмеченных недостатков лишены методы дискретного геометрического моделирования [11].
Геометрический объект произвольной формы всегда может быть представлен упорядоченным множеством точек по определенному закону так, чтобы можно было определить координаты любой точки внутри контура (области). Вопросом является лишь необходимая плотность исходной информации, затраты на ее получение, обработку и хранение.
Поэтому очевидной является необходимость проведения исследований дискретного формирования геометрических объектов, которые в своей основе обеспечивали бы необходимую точность построения модели геометрического образа при рациональном уменьшении объема исходной информации и минимальных затратах на получение конечного результата.
Анализ последних исследований. Наиболее перспективным направлением развития прикладной геометрии в современный период является дискретное геометрическое моделирование. Среди самых распространенных направлений в области дискретного моделирования поверхностей является метод конечных элементов, базирующийся на дискретном представлении поверхности в виде совокупности отдельных элементов, которые взаимодействуют между собой в конечном количестве узловых точек.
Метод конечных разностей выгодно отличается от метода конечных элементов простотой, но проигрывает в универсальности и точности результатов, которые получают при решении инженерной задачи.
На основе статической интерпретации метода конечных разностей профессором С.М. Ковалевым [9] создан статико-геометрический метод формообразования дискретных геометрических образов с определенными свойствами, который является наиболее наглядным и понятным методом дискретного моделирования непрерывных образов и в целом ряде случаев учитывает статическую особенность разных объектов.
Последующему развитию статико-геометрического метода, расширению его формообразующих свойств на основе анализа рекуррентных формул числовых последовательностей для дискретного моделирования и формирования дискретных образов объектов машиностроения и строительства посвящена докторская диссертация проф. С.И. Пустюльги [10], работы проф. С.Н. Ковалева [6, 8], а также ряд других работ. Результаты, полученные в этих исследованиях, показали новые возможности дискретного геометрического моделирования, в частности возможность простого перехода от дискретно представленного образа к его непрерывному аналогу и наоборот. В статьях [2, 3, 4] проведены исследования свойств и обобщение перехода от непрерывных зависимостей к рекуррентным формулам задания дискретных числовых последовательностей путем замены дискретными непрерывных параметров классов элементарных функциональных зависимостей обратных к ним, а также тех, которые получают из этих функций с помощью четырех арифметических действий и суперпозиций, примененных определенное количество раз.
Каждый из названных методов имеет свои преимущества и недостатки относительно решения конкретных практических задач. Поэтому их исследование, обогащение новыми эффективными алгоритмами, изучение возможности их компиляции, а на этой основе расширения множества исходных данных является актуальными. Также актуальным является последующее развитие и совершенствование вышеназванных методов в целом. При этом, с одной стороны можно обогатить известные методы дискретного геометрического моделирования новыми алгоритмами, усовершенствовать их моделирующие возможности, а с другой — расширить круг практических задач и оптимизировать создаваемые для их реализации модели.
В статье [5] профессор С.М. Ковалев определил понятие «суперпозиции» в прикладной геометрии на основе функционального сложения как суперпозиции множеств, между точками которых установлено определенное соответствие.
Постановка задания работы заключается в определении подходов к созданию новой теории дискретного моделирования геометрических объектов с помощью геометрического аппарата суперпозиций. Конкретно — необходимо, на первом этапе, разработать алгоритмы определения дискретных геометрических образов с использованием геометрического аппарата суперпозиций одномерных точечных множеств.
Изложение основного материала исследования.
Обобщая понятие «суперпозиции» на основе функционального сложения, можно говорить о суперпозиции множеств, между точками которых установлено некоторое соответствие. С такой точки зрения суперпозиция соответственных точек n множеств в m-пространстве в декартовой системе координат определяется системой уравнений [9]:
 (1)
(1)
где: i — номер координатной оси;
j — номер исходного множества суперпозиции;
ki,j -— коэффициент суперпозиции.
Суперпозиция B n совпавших соответственных точек ![]() совпадает с этими точками, если сумма коэффициентов суперпозиции равна единице (рис. 1) .
совпадает с этими точками, если сумма коэффициентов суперпозиции равна единице (рис. 1) .

Рисунок 1. Совмещенные поля точек
На рис. 2 дискретно представлена кривая линия точками с равномерным шагом h=1 вдоль оси Ox : ![]() .
.
Эта кривая может быть определена конечными разностями: правыми — ![]() , левыми –
, левыми – ![]() или центральными; например
или центральными; например

Рисунок 2 Дискретная модель параболы второго порядка
центральная разность четвертого порядка будет симметричной относительно узла
Bi : ![]() , а правая конечная разность n-го порядка
, а правая конечная разность n-го порядка
имеет вид ![]() , или
, или ![]() , где
, где ![]() – число соединений из n по k [10].
– число соединений из n по k [10].
Числовая последовательность, произвольный член которой определяется формулой в замкнутой форме ![]() , описывает параболу n-го порядка
, описывает параболу n-го порядка ![]() . Например, рекуррентная формула числовой последовательности:
. Например, рекуррентная формула числовой последовательности: ![]() имеет вид
имеет вид ![]() и является дискретным аналогом параболы второго порядка (рис. 1).
и является дискретным аналогом параболы второго порядка (рис. 1).
Для построения представленной на рис. 1 дискретной модели кривой с равномерным шагом h=1 вдоль оси Ox, которая проходит через точку A(xA=3;yA=4), B(xB=5;yB=0), C(xC=7;yC=4), статико-геометрическим методом необходимо составить и решить систему уравнений равновесия внутренних узлов
 (2)
(2)
При ![]() получим
получим ![]() ,
, ![]() ,
, ![]() .
.
Выше были рассмотрены примеры дискретного определения полинома второй степени тремя известными методами.
Во всех известных методах дискретного геометрического моделирования координаты узлов моделируемых дискретных аналогов кривых определяются по известным координатам смежных узлов. Дискретно представленные кривые (ДПК) задаются координатами узлов с равномерным шагом по оси.
Данные алгоритмы могут быть значительно эффективнее за счет экономии вычислительных ресурсов при формировании ДПК узлами с произвольными шагами вдоль оси по данным координатам произвольных узлов.
Дискретно определить представленную на рис. 2 кривую можно, используя следующее свойство [1]:
Координаты любой точки параболы n-го порядка являются суперпозицией (4) координат других точек этой параболы.
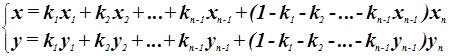 (3)
(3)
Запишем систему уравнений для точек заданной кривой
 (4)
(4)
Найдем коэффициенты суперпозиции k1, k2, решив данную систему
 (5)
(5)
Результаты вычислений коэффициентов суперпозиции точек F, B, N для определения точек кривой с равномерным шагом h=1 вдоль оси Ox, представленной на рис. 1 приведены в таблице 1.
Таблица 1.
Значения коэффициентов суперпозиции
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим возможности перехода от аналитических выражений полиномов разных степеней к рекуррентным формулам задания дискретных числовых последовательностей, определяя рекуррентную зависимость между произвольными членами числовой последовательности, взятыми с неравномерным шагом вдоль оси с помощью геометрического аппарата суперпозиций.
Числовая последовательность, произвольный член которой определяется формулой в замкнутой форме
![]() , (6)
, (6)
определяет полином n-й степени
![]() . (7)
. (7)
При n=1 последовательность имеет вид
![]() . (8)
. (8)
Такую последовательность, в свою очередь, определяет рекуррентная зависимость
![]() , (9)
, (9)
что является дискретным аналогом полинома первой степени.
Рекуррентная зависимость между последовательными членами последовательности второго порядка, взятыми с равномерным шагом, имеет вид
![]() (10)
(10)
и так далее — до n-го порядка [7] .
Определим рекуррентную зависимость между непоследовательными членами числовой последовательности, взятыми с неравномерным шагом.
Для последовательности первого порядка (рис. 3)
![]()
![]()

 (11)
(11)
 (12)
(12)
 (13)
(13)
 (14)
(14)

Рисунок 3. Последовательность 1-го порядка
 (15)
(15)
![]() .
.
Аналогично для последовательности второго порядка :
![]()
![]() (16)
(16)
Получаем выражения для определения k1, k2, k3:
 (17)
(17)

И потому рекуррентная зависимость будет иметь вид
 (18)
(18)
Проверим верность выведенных формул на конкретном примере. Рассмотрим определение аналитического выражения полинома второй степени:
![]()
по трем заданным точкам A, B, C с такими координатами:
A (1, 5); B (2, 1); C (5, 3).
Для нахождения m0, m1, m2 необходимо решить систему


Получаем аналитическое выражение данного полинома:
![]() (19)
(19)
и, соответственно, числовой последовательности:
![]() (20)
(20)
Ряд значений этой последовательности приведен в таблице 2.
Таблица 2.
Значения числовой последовательности
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определим ai+p по таким данным: p=1; p1=3; p2=7; p3=10.
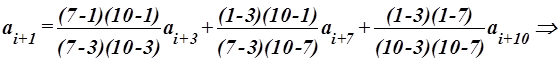
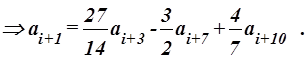
При i=0

Согласно данных, приведенных в таблице 1 a1=5; a3=-0,67; a7=16; a10=53
поэтому

При i=1

Согласно данных, приведенных в таблице 1 a2=1; a4=0; a8=26; a11=70
поэтому

Для последовательности n-го порядка :
![]()
рекуррентная зависимость имеет вид

Коэффициенты суперпозиции, которой определяются аналогично.
Выводы. В статье приведены результаты определения дискретных образов кривых линий с использованием геометрического аппарата суперпозиций одномерных точечных множеств. Для геометрического моделирования дискретных образов объектов строительства и машиностроения, могут быть применены разработанные алгоритмы перехода от замкнутой к рекуррентной форме задания числовой последовательности произвольными дискретными значениями.
Фундаментальные системные исследования геометрических свойств аппарата суперпозиции для формирования дискретных образов в сочетании с классическими численными методами, известными методами дискретного моделирования и преобразований позволят открыть новые возможности при решении конкретных прикладных задач в разных областях науки, техники и производства.
Список литературы:
1.Воронцов О.В., Радченко Г.О. Дискретне визначення кривих на основі різних методів геометричного моделювання / О.В. Воронцов, Г.О. Радченко // Прикладна геометрія та інженерна графіка. К.: КНУБА, — 2011. — Вип. 88. — С. 116—120.
2.Воронцов О.В. Дослідження рекурентних форм представлення елементарних функціональних залежностей / О.В. Воронцов, Г.О. Радченко // Прикладна геометрія та інженерна графіка. К.: КНУБА, — 2011. ― Вип. 87. ― С. 98―101.
3.Воронцов О.В. Заміна неперервних форм елементарних функціональних залежностей рекурентними формулами задання дискретних числових послідовностей / О.В. Воронцов // Геометричне та комп’ютерне моделювання: збірник наук. праць. Харків: ХДУХТ, — 2010. — Вип. 27. ― С. 57―62.
4.Воронцов О.В. Рекурентні аналоги класів елементарних функцій / О.В. Воронцов, Г.О. Радченко // Прикладна геометрія та інженерна графіка. К.: КНУБА, — 2010. ― Вип. 83. ― С. 136―139.
5.Ковалев С.Н. О суперпозициях / С.Н. Ковалев // Прикладна геометрія та інженерна графіка. К.: КНУБА, — 2010. — Вип. 84. — С. 38—42.
6.Ковалев С.Н. Прикладная геометрия и геометрическая статика / С.М. Ковальов, В.А. Вязанкин // Прикладна геометрія та інженерна графіка. К.: КНУБА, — 2007. ― Вип. 78. ― С. 41―43.
7.Ковальов С.М., Гумен М.С., Пустюльга С.І., Михайленко В.Є., Бурчак І.Н. Прикладна геометрія та інженерна графіка. Спеціальні розділи. Випуск 1. Луцьк.: Редакційно-видавничий відділ ЛДТУ, 2006. — С. 118—176.
8.Ковальов С.М. Рекурентні формули числових послідовностей у формуванні дискретно визначених геометричних образів / С.М. Ковальов, С.І. Ботвіновська // Прикладна геометрія та інженерна графіка. К.: КНУБА, — 2006. ― Вип. 76. ― С. 30―37.
9.Ковалев С.Н. Формирование дискретных моделей поверхностей пространственных архитектурных конструкций: Дис. … доктора техн. наук: 05.01.01 / С.Н. Ковалев. М., 1986 — 348 с.
10. Пустюльга С.І. Дискретне визначення геометричних об’єктів числовими послідовностями: Дис. … доктора техн. наук: 05.01.01 / С.І. Пустюльга. К., 2006. — 322 с.
11. Самостян В.Р. Вплив геометричних вимог на процеси дискретного моделювання криволінійних об’єктів будівництва: Дис. …канд. техн. наук: 05.01.01 / В.Р. Самостян. К., 2011. — 182 с.
дипломов


Оставить комментарий