Статья опубликована в рамках: XXXVIII Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 24 сентября 2014 г.)
Наука: Технические науки
Секция: Транспорт и связь, кораблестроение
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
ПОСТРОЕНИЕ ИНДЕКСА ПРОИЗВОЛЬНОГО ПРОЦЕССА
Босов Аркадий Аркадиевич
д-р техн. наук, профессор кафедры «Прикладная математика», Днепропетровский национальный университет железнодорожного транспорта имени академика В. Лазаряна, Украина, г. Днепропетровск
E -mail: AABosov@i.ua
Лоза Петр Алексеевич
канд. техн. наук, доцент кафедры «Электроподвижной состав железных дорог», Днепропетровский национальный университет железнодорожного транспорта имени академика В. Лазаряна, Украина, г. Днепропетровск
E-mail:
CREATION OF AN INDEX OF ARBITRARY PROCESS
Arkady Bosov
doctor of Engineering, professor of department «Applied mathematics», Dnipropetrovsk national university of railway transport named after academician V. Lazaryan, Ukraine, Dnepropetrovsk
Peter Loza
candidate of Science, associated professor of department «Electric rolling stock of the railroads», Dnipropetrovsk national university of railway transport named after academician V. Lazaryan , Ukraine, Dnepropetrovsk
АННОТАЦИЯ
В предлагаемой работе осуществляется объединение двух методов: метода главных компонент и метода анализа иерархий.
Предложен алгоритм построения индекса по наблюдаемым показателям.
При построении индекса произвольного процесса удалось избавиться от субъективизма экспертов используя метод анализа иерархий.
Если процесс является управляемым, то получаем возможность оценки, как принимавшихся решений, так и определения рациональных решений в определенном смысле на исследуемый процесс.
ABSTRACT
In offered work is carried out join of two methods: method of the principal components and method of the analysis of hierarchies.
The algorithm of creation of an index of observed indexes is offered.
At creation of an index of the arbitrary process, succeeded to get rid of subjectivity of experts, using a method of the analysis of hierarchies.
If process is operated, we have an assessment opportunity, both made decisions, and definition of rational decisions in a sense of studied process.
Ключевые слова: метод главных компонент; анализ иерархий; индекс процесса.
Keywords: method of the principal components; analysis of hierarchies; process index.
Многие процессы или явления, протекающие во времени, характеризуются несколькими показателями, и тогда возникает задача, с помощью линейных преобразований, определить такие показатели, которые между собой не коррелировали, но незначительное их число с достаточной степенью точности описывало бы исходный процесс.
Пусть в любой момент времени некоторый процесс характеризуется набором показателей ![]() .
.
Тогда возникает задача введения некоторого индекса, который бы с определенной степенью точности отражал бы поведение процесса во времени.
Если в моменты времени ![]() фиксировались значения показателей, то располагаем матрицей значений показателей. Данная матрица имеет
фиксировались значения показателей, то располагаем матрицей значений показателей. Данная матрица имеет ![]() строк и
строк и ![]() столбцов, а
столбцов, а ![]() будет представлять собой значение показателя
будет представлять собой значение показателя![]() в момент времени
в момент времени ![]() .
.
Процедура построения индекса будет состоять из двух этапов.
На первом этапе с помощью линейных преобразований переменных ![]() определяются новые показатели
определяются новые показатели ![]() такие, что они между собой не коррелируют [5].
такие, что они между собой не коррелируют [5].
Другими словами, основными являются соотношения
![]() (1)
(1)
или в матричной форме
![]() (2)
(2)
Как показано в работе [1] первоначально приходим к переменным ![]() , которые удовлетворяют равенствам
, которые удовлетворяют равенствам
![]() ,
,
где: ![]() — ортогональная матрица.
— ортогональная матрица.
Если ![]() первый столбец матрицы
первый столбец матрицы ![]() , то его выбираем так, чтобы дисперсия
, то его выбираем так, чтобы дисперсия ![]() была бы максимальной. После чего выбираем второй столбец
была бы максимальной. После чего выбираем второй столбец ![]() , так чтобы дисперсия
, так чтобы дисперсия ![]() была бы максимальной, и выполнялось условие некоррелированности
была бы максимальной, и выполнялось условие некоррелированности ![]() с
с ![]() .
.
Аналогично процедура продляется далее, и если мы работаем с ![]() , то накладывается условие некоррелированности
, то накладывается условие некоррелированности ![]() с
с ![]() .
.
Если ![]() дисперсия
дисперсия ![]() , а
, а ![]() ковариационная матрица
ковариационная матрица ![]() , то учитывая
, то учитывая
![]()
получим
![]() .
.
Поскольку ![]() некоррелированная, то имеет место
некоррелированная, то имеет место
![]() ,
,
а это означает, что матрица
![]()
является диагональной с элементами ![]() .
.
Более того имеет место
![]() ,
,
тогда нормируя ![]() получаем
получаем ![]() -тую главную компоненту
-тую главную компоненту ![]() .
.
Соотношение (2) теперь можно записать в виде
![]() ,
,
т. е. матрица ![]() будет следующей
будет следующей
![]() .
.
Если вместо ковариационной матрицы ![]() использовать корреляционную, то тогда имеет место
использовать корреляционную, то тогда имеет место
![]() .
.
Выбирая первые ![]() главных компонент, получим, что они описывают следующую долю разброса исходных показателей
главных компонент, получим, что они описывают следующую долю разброса исходных показателей
![]() ,
,
тогда вместо ![]() вводя
вводя ![]() главных компонент с заданной точностью описываем изучаемый процесс.
главных компонент с заданной точностью описываем изучаемый процесс.
На втором этапе производим линейную свертку ![]() главных компонент по методу анализа иерархий [4].
главных компонент по методу анализа иерархий [4].
Существенным элементом данного метода является построение матрицы попарных сравнений ![]() , элементы которой должны обладать свойствами:
, элементы которой должны обладать свойствами:
1) все ![]()
2) все ![]()
3) все ![]() (свойство совместности);
(свойство совместности);
4) максимальное собственное значение матрицы ![]() должно быть равно
должно быть равно ![]() .
.
В работе [2] показано, что если задана первая строка матрицы ![]() т. е.
т. е. ![]() то положив
то положив  все четыре свойства матрицы
все четыре свойства матрицы ![]() будут выполнены, а компоненты собственного вектора с максимальным собственным значением вычисляются по формуле
будут выполнены, а компоненты собственного вектора с максимальным собственным значением вычисляются по формуле
 .
.
Если ![]() главные компоненты, определяемые по методу главных компонент, а
главные компоненты, определяемые по методу главных компонент, а ![]() дисперсии разброса описываемые главными компонентами, то положив первую строку матрицы
дисперсии разброса описываемые главными компонентами, то положив первую строку матрицы ![]() по формуле
по формуле
![]()
получаем возможность вычисления ![]() , и после нормировки индекс процесса будет равным
, и после нормировки индекс процесса будет равным
![]() . (3)
. (3)
Таким образом, комбинируя метод главных компонент и метод анализа иерархий, получаем индекс процесса (3) как некоторую функцию исходных показателей.
В качестве примера рассмотрим индекс социальных последствий работы железной дороги. Показатели их значения за период с 2001 по 2012 годы представлены в Таблице 1.
Таблица 1.
Справка о выделении средств железной дорогой на социальные нужды (тыс. грн.)
|
№ п/п |
Наиме нование |
год |
|||||||||||
|
2001 |
2002 |
2003 |
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
2011 |
2012 |
||
|
1 |
Численность работников, чел. |
67 618 |
66 066 |
66 045 |
65 047 |
64 922 |
64 837 |
63 375 |
63 757 |
62 298 |
61 122 |
60 445 |
58 654 |
|
2 |
Фонд оплаты труда, тыс. грн. |
435 020 |
549 822 |
656 933 |
766 582 |
903 139 |
114 0860 |
1403 447 |
1835 556 |
188 3050 |
209 8018 |
2371 558 |
2646 323 |
|
3 |
Средняя заработная плата, грн. |
536 |
694 |
829 |
982 |
1159 |
1466 |
1845 |
2399 |
2519 |
2860 |
3270 |
3760 |
|
4 |
Производи тельность труда, тыс. т-км на 1 работн. |
1163 |
1154 |
1279 |
1320 |
1271 |
1329 |
1546 |
1516 |
1252 |
1388 |
1541 |
1556 |
|
5 |
Материальная помощь не работающим, грн |
9946 |
22602 |
21751 |
29403 |
30392 |
18255 |
12308 |
17274 |
14504 |
14248 |
16515 |
27059 |
|
6 |
Материальная помощь на оздоровление, грн |
7020 |
7823 |
11027 |
12628 |
17930 |
22030 |
28608 |
37712 |
44165 |
54206 |
58634 |
64990 |
|
7 |
Оказание мат. помощи при выходе на пенсию |
6660 |
5596 |
2930 |
4414 |
5250 |
8769 |
14245 |
18829 |
21472 |
21490 |
76277 |
23869 |
|
8 |
Финансовая поддержка оздоровит. спортивно-культурным заведениям, детским жел. дорогам |
2278 |
6662 |
5970 |
6332 |
11464 |
12739 |
20600 |
18947 |
20132 |
22886 |
24860 |
28854 |
|
9 |
Мат. помощь медицинским заведениям |
3960 |
3987 |
3490 |
11418 |
9834 |
8634 |
9945 |
10001 |
13246 |
13640 |
13965 |
12744 |
|
0 |
Мат. помощь учебным заведениям |
1832 |
2737 |
7798 |
19437 |
2325 |
1668 |
425 |
94 |
37 |
148 |
0 |
0 |
|
11 |
Бесплатные билеты для личных потребностей работающих |
0 |
0 |
0 |
0 |
10237 |
10802 |
11170 |
13728 |
18124 |
18519 |
24729 |
34060 |
|
12 |
Бесплатные билеты для личных потребностей неработающих |
0 |
0 |
0 |
0 |
3634 |
3415 |
3600 |
3725 |
4852 |
5257 |
6764 |
4062 |
|
13 |
Отчисления профсоюзу, в том числе |
6316 |
5131 |
4996 |
8997 |
11343 |
20750 |
21362 |
25917 |
24281 |
27255 |
29345 |
31490 |
|
14 |
-отчисления профсоюзным орг. на провед. культ.-масс. и спортивной работы |
546 |
1641 |
2882 |
4337 |
5382 |
6132 |
6192 |
7800 |
7195 |
7695 |
8282 |
8295 |
|
15 |
-удешевление стоимости путевок в оздоровит. учреждения железной дороги |
1284 |
2190 |
1196 |
3847 |
4463 |
8003 |
12412 |
13723 |
13288 |
15360 |
16671 |
17991 |
|
16 |
- санаторные путевки |
1150 |
1300 |
918 |
813 |
1498 |
1738 |
2758 |
3000 |
3500 |
4200 |
4392 |
5204 |
Как следует из таблицы 1, число показателей ![]() , а число наблюдений (годов)
, а число наблюдений (годов) ![]() .
.
При числе наблюдений равных 12, критический коэффициент корреляции ![]() (см. [3] таблица XII)
(см. [3] таблица XII)
Задавшись долей описываемого разброса данных ![]() , по методу главных компонент определяем число главных компонент, которые описывают 16 показателей.
, по методу главных компонент определяем число главных компонент, которые описывают 16 показателей.
На рисунке 1 представлены три главные компоненты.
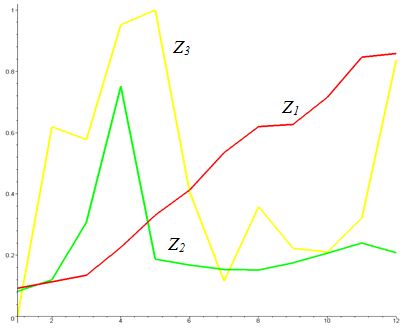
Рисунок 1. Главные компоненты
Компонента ![]() описывает
описывает ![]() разброса данных, а
разброса данных, а ![]() имеет
имеет ![]() , компонента
, компонента ![]() имеет
имеет ![]() .
.
Далее используем метод анализа иерархий, полагая
![]() ,
,
которым соответствуют следующие веса главных компонент
![]()
С помощью данных весов строим индекс социальных последствий по формуле
![]()
График данного индекса представлен на рисунке 2.

Рисунок 2 Индекс социальных последствий работы железной дороги в период с 2001 по 2012 годы
Как следует из рисунка 2, начиная с 2004 года, имеет место падение индекса по 2007 год, а с 2007 года индекс постепенно возрастает. Хотя с 2008 по 2009 год он незначительно упал, а далее наблюдается его рост.
Отмеченные колебания вполне можно объяснить ситуациями в стране, которые происходили в рассматриваемый период времени.
В итоге, можно сказать, что для дискретных процессов предложен метод построения его индекса. Данный метод представляет собой комбинацию метода главных компонент и метода анализа иерархий. В предлагаемом методе исключается субъективизм экспертов, с помощью использования дисперсий для главных компонент.
Предложенный метод используется для расчета индекса социальных последствий работы железной дороги.
Данный метод может быть использован для оценки мероприятий, посвященных социальной сфере и определения такого набора мероприятий, которые укладываются в заданные объемы финансирования и максимально улучшающих социальную сферу.
Список литературы:
1.Лоули Д. Факторный анализ как статистический метод / Д. Лоули, А. Максвелл. М.: Мир, 1967. — 144 с.
2.Ногин В.Д. Упрощенный вариант метода анализа иерархий на основе нелинейной свертки критериев / В.Д. Ногин. СПб., 2004. — 16 с.
3.Плохинский Н.А. Биометрия. / Н.А. Плохинский Из-во Московского университета, 1970, — 367 с.
4.Саати Т. Принятие решений: метод анализа иерархий. / Т. Саати. М.: Радио и связь, 1993. — 320 с.
5. Pearson K. On lines and planes of closest fit to system of points in space. Phil. Mag.2, 6th series, 1901, — p. 557—572.
дипломов


Оставить комментарий