ПОСТРОЕНИЕ  ПАРКЕТОВ  С  ПОМОЩЬЮ  ГЕОМЕТРИЧЕСКИХ  ПРЕОБРАЗОВАНИЙ

Ненастина  Ольга

Класс  6  «Д»,  МБОУ  СОШ  №  89  МО 
РФ,  г.  Краснодар

Колчанов  Андрей  Викторович

научный  руководитель,  учитель  математики  МБОУ  СОШ  №  89  МО 
РФ,  г.  Краснодар

Актуальность  темы.  В  последнее  время  использование  мотивов  различных  паркетов  в  одежде,  аксессуарах,  дизайне  жилища,  строительстве  зданий  является  последним  «писком»  моды.  Математическая  теория  паркетов  имеет  свое  практическое  применение:  знание  её  основ  будет  полезно  дизайнерам,  строителям,  людям,  увлекающимся  народными  ремёслами.  Поэтому  актуальность  данной  работы  не  вызывает  сомнения. 

Целью  данной  работы  является  разработка  принципов  построения  сложных  паркетов  и  создание  эскизов  паркетов  из  симметричных  фигур  с  помощью  геометрических  преобразований  плоскости.

Геометрические  паркеты.

Понятие  паркета  в  геометрии  тесно  связано  с  процессом  замощения  плоскости.

Паркет  –  замощение  плоскости  многоугольниками  без  пробелов  и  перекрытий,  в  котором  любые  два  многоугольника  имеют  либо  общую  сторону,  либо  только  общую  вершину,  либо  вовсе  не  имеют  общих  точек  [4].

Паркеты,  составленные  из  одинаковых  правильных  многоугольников,  называют  правильными  паркетами. 

Паркеты,  состоящие  из  правильных  многоугольников  двух  или  более  типов,  такие,  что  для  любых  двух  вершин  паркета  существует  преобразование  симметрии  (самосовмещение),  переводящее  одну  из  них  в  другую,  называются  полуправильными  паркетами  или  архимедовыми  паркетами  [5].

Рассмотри  некоторые  виды  геометрических  преобразований  плоскости.

1.  Центральная  симметрия  –  это  геометрическое  преобразование  плоскости,  при  котором  точка  А  переводится  в  некоторую  точку  А₁,  так,  что  О  –  середина  отрезка  АА₁.  В  этом  случае  говорят,  что  О  –  центр  симметрии  [1].

2.  Осевая  симметрия  –  это  геометрическое  преобразование  плоскости,  при  котором  множеством  неподвижных  точек  является  прямая,  называемая  осью  симметрии.  Из  определения  следует,  что  любой  точке  соответствует  точка,  находящаяся  на  том  же  расстоянии  от  оси  симметрии  [1].

3.  Вращательная  симметрия  –  это  геометрическое  преобразования  плоскости,  означающее  симметрию  объекта  относительно  некоторых  собственных  вращений  [2].

4.  Симметрия  относительно  плоскости  –  это  такое  свойство  геометрической  фигуры,  когда  любой  точке,  расположенной  по  одну  сторону  плоскости,  всегда  будет  соответствовать  точка,  расположенная  по  другую  сторону  плоскости,  а  отрезки,  соединяющие  эти  точки,  будут  перпендикулярны  плоскости  симметрии  и  делятся  ею  пополам.  Зеркально  симметричным  считается  объект,  состоящий  из  двух  половин,  которые  являются  зеркальными  двойниками  по  отношению  друг  к  другу.  Трехмерный  объект  преобразуется  сам  в  себя  при  отражении  в  зеркальной  плоскости,  которую  называют  плоскостью  симметрии  [2].

Построение  паркета  с  помощью  параллельного  переноса.  Наглядно  параллельный  перенос  определяется  как  преобразование  плоскости,  при  котором  точки  смещаются  в  одном  и  том  же  направлении  на  одно  и  тоже  расстояние. 

Построим  паркет  с  использованием  параллельного  переноса.

Алгоритм  построения:

1.  Возьмем  несколько  симметричных  фигур. 

2.  Преобразуем  композицию  фигур 

3.    Выполняем  параллельный  перенос  в  соответствующем  направлении,  отмеченном  стрелками  для  каждой  из  фигуры.

Стрелками  указаны  направления  параллельного  переноса  для  каждой  фигуры. 

4.  Преобразуем  получившийся  рисунок  с  помощью  параллельного  переноса.  Получим  паркет.

Построение  паркета  с  помощью  центральной  симметрии.

1.  Выбираем  несколько  центрально-симметричных  фигур,  разных  по  цветовой  гамме,  имеющих  одинаковую  длину  сторон  и  составляем  рисунок;

2.                     Составляем  с  помощью  табличного  процессора  Microsoft  Excel  рисунок,  используя  графические  возможности;

3.  Выбираем  центр  симметрии  и  строим  симметричную  фигуру  относительно  центра  О;

4.  Преобразуем  с  помощью  зеркального  отображения,  получившийся  рисунок;

Подвергаем  параллельному  переносу  и  получаем  новый  паркет.

Построение  паркета  с  помощью  осевой  симметрии  и  зеркального  отображения.

1.  Построим  центрально  симметричные  фигуры:

2.  Из  числа  выбранных,  одинаковых  по  размеру  центрально-симметричных  фигур,  но  разных  по  цветовой  гамме  составляем  рисунок  в  табличном  процессоре  Microsoft  Excel  ;

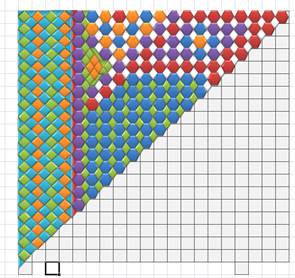
3.  Отображаем  фигуру  относительно  оси  симметрии  L.

4.  Преобразуем  получившуюся  фигуру  с  помощью  осевой  симметрии  относительно  центра  О. 

5.  Преобразуем  полученную  фигуру  относительно  горизонтальной  оси  симметрии,  получаем  новый  паркет.

В  работе  над  данной  темой  мы:  расширили  свой  математический  кругозор,  изучили  основы  построения  паркетов  из  различных  геометрических  фигур,  с  помощью  геометрических  преобразований,  разработали  на  примере  центрально-симметричных  фигур  собственные  паркеты  и  реализовали  их  табличном  процессоре  Microsoft  Excel. 

Чтобы  выяснить,  насколько  интересна  учащимся  выбранная  тема,  мы  провели  конкурс  геометрических  паркетов  среди  62  учеников  из  МБОУ  СОШ  №89  в  рамках  изучения  темы  «Центральная  и  осевая  симметрия».

Процесс  выполнения  исследования  и  полученные  результаты  доказывают  значимость  проделанной  работы,  а  она  заключается  в  следующем:

1.  закреплены  имеющиеся  теоретические  знания,  найдена  их  практическая  реализация;

2.  использование  результатов  проведения  математического  анализа  возможно  в  различных  областях;

3.  синтезированы  знания,  полученные  в  ходе  работы,  теоретические  знания  из  курса  геометрии,  которые  должны  помочь  при  применении  данных  технологий  в  укладке  паркета.

Материалы  работы  будут  полезны  и  интересны  на  уроках  математики  при  изучении  тем:  «Правильные  многоугольники»,  «Центральная  симметрия»,  «Осевая  симметрия»,  «Геометрические  тела»,  а  также  их  можно  использовать  на  уроках  изобразительного  искусства  и  черчения.

Список  литературы:

1. Колмогоров  А.Н.  Паркеты  из  правильных  многоугольников.  Журнал  “Квант”  №  3,  1970  г.
2. Математика.  6  кл.:  учебник  /  Г.К.  Муравин,  О.В.  Муравина.  –  3-е  издание.,  стереотип.  –  М.:  Дрофа,  2015.  –  319,  [1]  c.  :  ил.
3. Скопец  З.А.  Геометрические  миниатюры./  Скопец  З.А.  М.:  1990. 
4. Энциклопедический  словарь  юного  математика.  –  М.:  Педагогика,  1985,  стр.  200–201.  .