ПОСТРОЕНИЕ  КВАДРАТА,  РАВНОСОСТАВЛЕННОГО  ДВУМ  ДАННЫМ,  И  ТЕОРЕМА  ПИФАГОРА

Уфимцев  Егор

Класс  8,  АНО  школа  «Шанс», 
РФ,  г.  Кемерово

Шугалов  Борис  Семенович

научный  руководитель,  канд.  физ.-мат.  наук,  доцент  КРИПКиПРО, 
РФ,  г.  Кемерово

Постановка  цели  исследования

В  прямоугольном  треугольнике  квадрат  гипотенузы  равен  сумме  квадратов  катетов.  В  равнобедренном  треугольнике  углы  при  основании  равны.

Какое  из  этих  двух  утверждений  представляются  более  простым,  очевидным? 

Если  заранее  не  знать  представленного  свойства  равнобедренного  треугольника,  то  можно  ли  ответить  на  вопрос  об  углах  при  основании,  догадаться  и  сформулировать  это  свойство?  А  как  связаны  между  собой  стороны  прямоугольного  треугольника?  Как  бы  вы  ответили  на  этот  вопрос,  не  зная  теоремы  Пифагора?  Взяв  прямоугольный  треугольник  с  катетами  5  и  12,  непосредственно  не  видно,  что  его  гипотенуза  точно  равна  13.  Теорема  Пифагора  представляется  как  более  глубокий  результат  в  изучении  свойств  геометрических  фигур. 

Цель  работы:  рассмотреть  задачи,  приводящие  к  формулировке  теоремы  Пифагора,  и  привести  соответствующие  доказательства.

1.  Как  из  двух  одинаковых  квадратов  составить  третий  квадрат

Возникновение  геометрии  как  науки  связано  с  измерением  площадей  земельных  участков.  Рассмотрим  пример.  Представим  два  одинаковых  квадратных  участка  земли.  А  нужно  отмерить  квадратный  участок,  площадь  которого  равна  сумме  площадей  двух  данных.  Чему  равна  сторона  третьего  квадратного  участка  земли?

Перейдём  от  земельных  участков  к  плоским  фигурам,  которые  можно  легко  разрезать  на  части,  и  изменим  формулировку  вопроса:

Даны  два  одинаковых  квадрата.  Как,  разрезая  их  на  части,  из  всех  полученных  частей  составить  третий  квадрат?

Рисунок  1.

Разрезав  каждый  квадрат  по  диагонали,  из  четырех  полученных  треугольников  составляется  третий  квадрат  (рис.  1  а).  Другой  способ  решения:  по  двум  диагоналям  разрезается  один  из  квадратов;  полученными  треугольниками  окружается  второй  из  данных  квадратов  (рис.  1  б).

Очевидно,  что  сторона  третьего  квадрата  равна  диагонали  исходных  квадратов.  А  значит,  переходя  к  земельным  участкам,  можно  отмерить  квадратный  участок,  площадь  которого  равна  сумме  площадей  исходных  участков.

2.  Обобщение  задачи  и  ее  решение  в  частном  случае

Даны  два  произвольных  (неравных)  квадрата.  Как,  разрезая  их  на  части,  из  всех  полученных  частей  составить  третий  квадрат?

Решим  эту  задачу  для  частного  случая,  когда  сторона  одного  из  квадратов  в  два  раза  больше  стороны  другого  квадрата.

Рисунок  2.

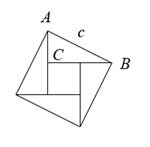
Рисунок  3.

Разрежем  больший  квадрат  на  два  равных  прямоугольника  и  эти  прямоугольники  –  по  диагонали.  Окружив  полученными  треугольниками  меньший  квадрат,  составим  третий  квадрат,  площадь  которого  равна  сумме  площадей  исходных  квадратов  (рис.  2).

Пусть  a,  b  –  длины  сторон  исходных  квадратов,  с  –  длина  стороны  третьего  квадрата;  a²,  b²,  c²  –  площади  соответствующих  квадратов.  Тогда  утверждение  о  площадях  принимает  вид:

  c²  =  a²  +  b².  (*)

Соотношение  (*)  можно  «прочитать»  иначе:  в  прямоугольном  треугольнике  АВС  (рис.  2),  один  из  катетов  которого  в  два  раза  больше  другого,  квадрат  гипотенузы  равен  сумме  квадратов  катетов.

3.  Обобщение  полученного  утверждения  –  теорема  Пифагора

А  если  взять  произвольный  прямоугольный  треугольник,  то  изменится  ли  соотношение  (*)  между  его  сторонами?

На  гипотенузе  произвольного  прямоугольного  треугольника  АВС  с  катетами  a  и  b  построим  квадрат  так,  чтобы  вместе  с  дополнительными  отрезками  получилась  фигура  аналогичная  составной  фигуре  рисунка  2  (рис.  3).  Прямоугольные  треугольники  этой  фигуры  равны  по  гипотенузе  и  прилежащим  к  ней  углам.  Внутренняя  часть  фигуры  –  квадрат  со  стороной  a  –  b  (a  >  b).  Поэтому  площадь  построенного  на  гипотенузе  квадрата  c²  равна  сумме  площадей  внутреннего  квадрата  (a–b)²  и  учетверённой  площади  исходного  треугольника  ab/2:

.  Отсюда  c²  =  a²  +  b².

Таким  образом,  соотношение  (*)  справедливо  для  любого  прямоугольного  треугольника.  Теорема  Пифагора  доказана.

4.  «Шарнирный»  способ  составления  квадрата  из  двух  данных

Вопрос  о  преобразовании  двух  произвольных  квадратов  в  один  остался  не  решенным.  Экономное  решение  этой  задачи  представлено  на  рис.  4  [2,  с.  106]. 

Рисунок  4.

Данные  квадраты  расположены  в  виде  фигуры  ABCDEF.  На  стороне  AF  отложен  отрезок  FQ  =  AB.  Фигура  разрезается  по  прямым  EQ  и  BQ.  Затем,  треугольник  BAQ  перекладывается  в  положение  ВСР,  а  треугольник  EFQ  –  в  положение  EDP.  Получается  квадрат  EQBP,  равносоставленный  двум  данным.

Действительно,  треугольники  ABQ  и  QFE  равны  по  двум  катетам:

АВ  =  FQ,  AQ  =  AF  –  FQ  =  AB  +  FE  –  AB  =  FE.

Отрезок  DP  –  часть  стороны  СР  треугольника  ВСР.

DP  =  AB  +  CP  –  EF  =  AB  +  AQ  –  EF  =  AB  =  QF,

то  есть  «выступающая»  часть  DP  треугольника  ВСР  равна  стороне  QF  треугольника  QFE,  помещаемого  в  положение  PDE.  Установлена  осуществимость  построения  четырёхугольника  EQBP.

  Из  равенства  прямоугольных  треугольников  ABQ  и  QFE  следует  равенство  всех  сторон  четырёхугольника  EQBP.  Поэтому  этот  четырёхугольник  –  параллелограмм.  И  при  этом  ÐBQE  =  180°  -  (ÐAQB  +  ÐFQE)  =  180°  -  (ÐAQB  +  ÐABQ)  =  90°.  А  значит,  параллелограмм  EQBP  –  прямоугольник.  По  определению,  прямоугольник,  у  которого  все  стороны  равны,  –  квадрат.  Таким  образом,  квадрат  EQBP  и  два  данных  квадрата  –  равносоставленные  фигуры. 

Представленный  способ  решения  называется  «шарнирным»,  так  как  треугольник  BAQ  принимает  положение  ВСР  при  его  повороте  вокруг  точки  В,  а  треугольник  EFQ  принимает  положение  EDP  при  повороте  вокруг  точки  Е  (рис.  4).

Из  данного  способа  построения  квадрата,  равносоставленного  двум  данным,  следует  и  теорема  Пифагора.

В  самом  деле,  начиная  с  произвольного  прямоугольного  треугольника  EFQ,  на  продолжении  FQ  за  точку  Q  отложим  отрезок  AQ  =  EF.  И  далее  строим  фигуру,  аналогичную  фигуре  на  рис.  4.  Площадь  квадрата  EQBP  равна  сумме  площадей  двух  других  квадратов.  А  это  значит,  что  квадрат  гипотенузы  EQ  прямоугольного  треугольника  EFQ  равен  сумме  квадратов  его  катетов.

5.  «Симметричный»  способ  составления  квадрата  из  двух  данных

Другое  разбиение  составного  квадрата,  представленного  на  рис.  3,  получается,  если  стороны  внутреннего  квадрата  продолжить  в  противоположном  направлении  (рис.  5  а).  При  таком  разбиении  внутренний  квадрат  окружают  четыре  равных  четырехугольника.  Из  этих  четырехугольников  можно  составить  квадрат  (рис.  5  б).

Рисунок  5.

Обращение  представленного  преобразования  (от  рис.  5  б  к  рис.  5  а)  приводит  к  другому  способу  составления  квадрата  из  двух  данных  [1,  с.  18].  Рассмотрим  это  решение.

Рисунок  6.

Рисунок  7.

На  рис.  6  ВК  –  сторона  меньшего  квадрата,  расположенного  на  стороне  АВ  большего  квадрата  ABCD.  Отрезок  АК  представляет  разность  сторон  данных  квадратов;  точка  М  –  середина  отрезка  АК.  Отложим  отрезок  АМ  от  вершин  В,  С,  D  на  сторонах  квадрата  ABCD.  Получим  точки  Q,  N,  P,  соответственно.  Соединим  точку  М  с  точкой  N,  а  точку  Р  с  точкой  Q.

Можно  доказать,  что  отрезки  MN  и  PQ  перпендикулярны,  пересекаются  в  центре  квадрата  (точка  О)  и  разбивают  его  на  четыре  равных  четырехугольника. 

Совершим  параллельный  перенос  четырехугольника  АМОР  по  направлению  PQ  на  величину  PQ,  четырехугольника  CNOQ  по  направлению  NM  на  величину  NM  (рис.  7).  Нижний  четырехугольник  DPON  перенесем  по  направлению  PQ  на  величину  PQ  (новое  положение  выделено  пунктиром),  а  затем,  -  по  направлению  NM  на  величину  NM.  Получим  квадрат  OEFG,  площадь  которого  равна  сумме  площадей  двух  исходных  квадратов.

Используя  представленное  решение,  докажем  теорему  Пифагора.

Пусть  СВК  прямоугольный  треугольник  (ÐВ  =  90°,  ВС  >  ВК).  На  катетах  треугольника  построим  квадраты:  один  из  них  –  ABCD  на  катете  ВС,  другой  –  на  катете  ВК  (рис.  7). 

Разбив  квадрат  ABCD,  как  было  показано,  на  четыре  четырехугольника  и  окружив  ими  меньший  квадрат,  получим  квадрат  OEFG,  площадь  которого  равна  сумме  площадей  квадратов,  построенных  на  катетах  треугольника  СВК  –  СВ²  +  ВК².

По  построению,  сторона  ОЕ  составного  квадрата  OEFG  равна  MN,  а  так  как  CKMN  –  параллелограмм  (КМ  =  CN  и  КМ  ççCN),  то  MN  =  СК.  Поэтому  площадь  квадрата  OEFG  равна  СК².  Таким  образом,  квадрат  гипотенузы  треугольника  СВК  равен  сумме  квадратов  его  катетов:

СК²  =  СВ²  +  ВК².

Заключение

При  установлении  равенства  площадей  многоугольников  используется  представление  о  равносоставленности  двух  фигур:  если  две  фигуры  можно  разрезать  на  одинаковые  наборы  частей,  то  эти  фигуры  называются  равносоставленными.  Равносоставленные  фигуры  равновелики  (имеют  одинаковую  площадь).

Задача  на  построение  квадрата,  равносоставленного  двум  данным,  уже  в  процессе  решения,  как  его  ответвление,  приводит  к  формулировке  и  доказательству  теоремы  Пифагора.  Представлены  два  различных  способа  решения  этой  задачи  -  «шарнирный»  и  «симметричный»  -  и  соответствующие  доказательства  теоремы  Пифагора.  Эти  доказательства  конструируются  как  обращение  построений,  приводящих  к  решению  задачи  на  составление  квадрата. 

Рассмотрение  вопроса  для  частного  случая,  когда  из  двух  данных  квадратов  сторона  одного  квадрата  в  два  раза  больше  стороны  другого,  приводит  и  к  теореме  Пифагора,  и  к  построению  квадрата,  равносоставленного  двум  данным,  в  общем  виде.  Переход  от  частного  к  общему  и  обращение  являются  общезначимыми  мыслительными  приемами  при  постановке  и  решении  разнообразных  исследовательских  задач.

Список  литературы:

1. Головина  Л.И.,  Яглом  И.М.  Индукция  в  геометрии.  –  М.:  Государственное  издательство  физико-математической  литературы,  1961.
2. Кордемский  Б.А.  Математическая  смекалка.  –  М.:  Государственное  издательство  технико-теоретической  литературы,  1955.