Статья опубликована в рамках: XI Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ЭКОНОМИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 23 мая 2013 г.)
Наука: Экономика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ КАК МЕТОД ОПТИМИЗАЦИИ ТРАНСПОРТНОГО МАРШРУТА (НА ПРИМЕРЕ ЖЕЛЕЗНОДОРОЖНЫХ ГРУЗОВЫХ ПЕРЕВОЗОК ПО МАРШРУТУ РОССИЯ-ПОЛЬША)
Мозолева Мария Вадимовна
студент 5 курса, кафедра Экономики и организации производства Московского государственного машиностроительного университета (МАМИ), г. Москва
E-mail: mvmozoleva@mail.ru
Макаренко Сергей Александрович
научный руководитель, старший преподаватель кафедры Экономики и организации производства Московского государственного машиностроительного университета (МАМИ), г. Москва
С расширением производства и увеличение экономического развития транспортные грузовые перевозки приобретают все большее значение в современном мире. Актуальность вопросов оптимизации маршрута и снижение стоимости перевозки выходит на первый план. Поскольку это позволяет снизить конечную стоимость товаров для конечных потребителей, снижать производственные запасы, повысить рентабельность бизнеса.
Цель данной работы является оптимизация транспортного маршрута грузовых перевозок, с помощью метода построения математической модели линейного программирования.
Проведем анализ существующих математических моделей по формированию перевозочных схем и критериев по оптимизации.
Под моделью понимается любое описание логистической системы, которое может быть использовано вместо нее для исследования ее свойств и прогнозирования возможных вариантов поведения.
Моделирование логистических систем можно проводить различным образом и приходить в итоге к разным моделям. Для того чтобы построить модель необходимо следовать следующим принципам:
·модель должна иметь поведение, структуру и функции, такую как у моделируемой логистической системы или ее компонента;
·отклонения параметров модели в процессе ее функционирования от соответствующих параметров моделируемой логистической системы не должны выходить за рамки допустимой точности моделирования;
·на основании исследования модели и ее поведения должно быть возможным обнаружить новые свойства моделируемой логистической системы, не содержащиеся в исходном материале, использованном для составления данной модели;
·проводить исследования и эксперименты на модели должно быть более удобно, чем на реальной логистической системе [1, с. 125].
Рассмотрим основные методы решения задач с применением математического моделирования и выберем тот, который наиболее удовлетворяет условиям для оптимизации транспортного потока (рис. 1).

Рисунок 1. Схема классификаций математических моделей
1. Динамическое программирование (динамическое планирование) представляет собой особый математический метод оптимизации решений, специально приспособленный к многошаговым (или многоэтапным) операциям. В динамическом программировании целесообразно оптимизировать операцию в целом, не разбивая ее на этапы, подлежащие пошаговому решению.
2. Моделирование операций по схеме марковских случайных процессов. Многие операции, которые приходится анализировать в контексте выбора оптимального решения, развиваются как случайные процессы, ход и исход которых зависят от ряда случайных факторов, сопровождающих эти операции.
3. Теория массового обслуживания. По мере исследования различных операций достаточно часто случается встречаться с анализом работы таких систем, как системы массового обслуживания (СМО). «Каждая СМО предназначена для обслуживания (выполнения) какого-то потока заявок, поступающих в какие-то случайные моменты времени» [5, с. 439].
4. Метод динамики средних элементов непосредственно изучает средние характеристики случайных процессов, протекающих в сложных системах с большим числом состояний. Основой применимости метода динамики средних является то, что препятствует изучению явлений более подробными методами: сложность изучаемых процессов и большое число участвующих в них элементов.
5. Моделирование операций методом статистических испытаний. «Для всяких потоков событий, перемещающих систему из состояния в состояние, решения аналитическим способом получены только для частных случаев, в общем же случае методов удовлетворяющих описанию процессов не существует» [2, с. 93].
6. Линейное программирование представляет собой направление математики, которое изучает методы решения задач, характеризующиеся линейной зависимостью между переменными и линейным критериями оптимальности. В данном случае программирование означает планирование, формирование планов, разработка программы действий. Этот метод наиболее приемлем для оптимизации транспортного потока, поскольку достаточно прост, удобен в применении и удовлетворяет условиям по оптимизации транспортного потока.
К задачам линейного программирования относят исследования конкретных производственно-хозяйственных ситуаций, которые в том или ином виде являются задачами оптимального использования ограниченных ресурсов.
Экономико-математическая модель, для решения задачи с помощью линейного программирования, включает в себя целевую функцию, где необходимо определить оптимальное значение (максимум или минимум), систему ограничений, а также требование, чтобы переменные были неотрицательными [4, с. 17].
В общем виде модель записывается следующим образом:
· целевая функция:
|
f ( |
(1) |
ограничения:
|
(2) |
· требование неотрицательности:
|
xj ≥ 0, j = |
(3) |
где: aij, bi, cj (i = ![]() , j =
, j = ![]() ) — заданные постоянные величины.
) — заданные постоянные величины.
Для решения задачи необходимо найти оптимальное значение функции (1) при соблюдении ограничений (2) и (3).
Систему ограничений (2) называют функциональными ограничениями задачи, а ограничения (3) — прямыми.
Вектор ![]() = (x1,x2,…,xn), который удовлетворяет ограничениям (2) и (3), является допустимым решением задачи линейного программирования. План вектора
= (x1,x2,…,xn), который удовлетворяет ограничениям (2) и (3), является допустимым решением задачи линейного программирования. План вектора ![]() * = (x1*,x2*,…,xn*), при котором функция (1) достигает своего максимального (минимального) значения, называется оптимальным [3, с. 41].
* = (x1*,x2*,…,xn*), при котором функция (1) достигает своего максимального (минимального) значения, называется оптимальным [3, с. 41].
Используем метод линейного программирования для решения конкретной задачи по транспортной перевозке груза (алюминий 10 тонн) из одной страны в другую (Россия-Польша) железнодорожным транспортом. В целях оптимизации процесса выбранного направления работы проведем анализ экономических и временных затрат по нескольким вариантам движения и определим наиболее выгодный. При этом применяются следующие критерии выбора оптимальной схемы перевозки:
·минимальные совокупные затраты на прохождение маршрута;
· минимальное расстояние от пункта загрузки в России (Москва) до пункта выгрузки в Польше (Варшава).
Железнодорожный поезд может двигаться по разным маршрутам от промежуточного склада к потребителю. Для определения расстояний пользуемся программным обеспечением Яндекс карты.
Принимаем провозную плату по каждому маршруту за ai, путевые расходы по каждому из маршрутов за bi, их сумма дает совокупные переменные затраты на выполнение рейса:
Li = ai + bi,
где: Li — совокупные переменные затраты на выполнение рейса.
Таким путем получаем линейную функцию:
Li = ai + bi → min,
где: ai — провозную плату при выполнении рейса по i-ому маршруту, руб.;
bi — путевые расходы при выполнении рейса по i-ому маршруту, руб.
Накладываем ограничения на данную линейную функцию.
1. Протяженность маршрута не должна превышать 1600 км:
S ≤ 1600,
где: S — протяженность маршрута, км.
2. Общие затраты на маршрут должны составлять не более 4500 долл. США:
a ≤ 4500
Получаем математическую модель:
Li = ai + bi → min, при ![]()
На основании изложенных выше условий для определения наиболее эффективных показателей рассмотрим следующие варианты транзита для определяемого маршрута:
1. Россия-Беларусь-Польша
2. Россия-Украина-Польша
3. Россия-Латвия-Литва-Польша
Маршрут № 1 Россия-Беларусь-Польша

Рисунок 2. Карта маршрута № 1
Таблица 1.
Провозная плата грузов
|
Страна |
Расстояние, км |
Провозная плата, долл. США |
Количество дней, сутки |
|
Россия |
542 |
1521,12 |
3+1 на отправление (СМГС) |
|
Беларусь |
622 |
5265,69 |
4 |
|
Польша |
187 |
897,38 |
1 |
|
Итого |
1351 |
7683,38 |
9 |
Таблица 2.
Путевые расходы на перевозку грузов, долл. США
|
Страны |
Различные сборы |
|
Россия |
180 |
|
Беларусь |
130 |
|
Польша |
28,31 |
|
Итого: |
338,31 |
L1 = a1 + b1 = 7683,38+338,31=8021,69
Проверим данную схему перевозки на соответствие заданным ограничениям согласно математической модели:
1. Протяженность маршрута не должна превышать 1600 км:
S= 1351
2. Общие затраты на маршрут должны составлять не более 4500 долл. США:
а = 8021,69
Поскольку ограничение оп общим затратам на маршрут не выполняется, можно сделать вывод, что параметры маршрута № 1 не удовлетворяют заданным критериям.
Маршрут № 2 Россия-Украина-Польша
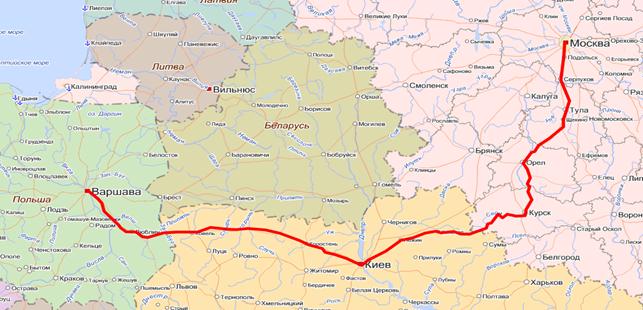
Рисунок 3. Карта маршрута № 2
Таблица 3.
Провозная плата грузов
|
Страна |
Расстояние, км |
Провозная плата, долл. США |
Количество дней, сутки |
|
Россия |
542 |
1521,12 |
3+1 на отправление (СМГС) |
|
Украина |
956 |
1751,81 |
5 |
|
Польша |
302 |
1325,71 |
2 |
|
Итого |
1800 |
4598,65 |
11 |
Таблица 4.
Путевые расходы на перевозку грузов, долл. США
|
Страны |
Различные сборы |
|
Россия |
230 |
|
Украина |
97,73 |
|
Польша |
38,18 |
|
Итого: |
365,91 |
L1 = a1 + b1 = 4598,65+365,91=4964,56
Проверим данную схему перевозки на соответствие заданным ограничениям согласно математической модели:
1. Протяженность маршрута не должна превышать 1600 км:
S= 1800
2. Общие затраты на маршрут должны составлять не более 4500 долл. США:
а = 4964,56
Поскольку ограничения протяженности маршрута и общих затрат не выполняется, можно сделать вывод, что параметры маршрута № 2 не удовлетворяют заданным критериям.
Маршрут № 3 Россия-Латвия-Литва-Польша

Рисунок 4. Карта маршрута № 3
Таблица 5.
Провозная плата грузов
|
Страна |
Расстояние, км |
Провозная плата, долл. США |
Количество дней, сутки |
|
Россия |
685 |
2197,59 |
4+1 на отправление (СМГС) |
|
Латвия |
185 |
160,13 |
1 |
|
Литва |
407 |
329,54 |
3+1 на отправку (СМГС) |
|
Польша |
279 |
1059,24 |
2 |
|
Итого |
1556 |
3746,5 |
12 |
Таблица 6.
Путевые расходы на перевозку грузов, долл. США
|
Страны |
Различные сборы |
|
Россия |
130 |
|
Латвия |
90 |
|
Литва |
73 |
|
Польша |
18,42 |
|
Итого: |
311,42 |
L1 = a1 + b1 = 3746,5+311,42=4057,92
Проверим данную схему перевозки на соответствие заданным ограничениям согласно математической модели:
1. Протяженность маршрута не должна превышать 1600 км:
S= 1556
2. Общие затраты на маршрут должны составлять не более 4500 долл. США:
а = 4057,92
Из приведенных выше маршрутов видно, что под заданные ограничения, согласно модели линейного программирования, подходит маршрут № 3.
Таким образом, на сегодняшний день увеличения стоимости топлива существенно влияет на увеличение стоимости перевозки груза. Следствием этого является рост конечной стоимости продукции и услуг для потребителя.
Следовательно, при рациональном выборе параметров перевозки можно существенно уменьшить расходы на транспортные услуги. Решив конкретную задачу по оптимизации транспортного процесса, можно сделать вывод о том, что с помощью метода построения математической модели линейного программирования, можно существенно оптимизировать перевозку грузов в различные страны.
Было построено несколько вариантов маршрутов. Для полученных маршрутов было рассчитано общее расстояние прохождения и затраты. При использовании маршрута № 3 расстояние сократилось на 1,8 %, по сравнению со вторым маршрутом, а также сократились расходы на перевозку грузов больше, чем в 2 раза, по сравнению с первым маршрутом и в 1,5 раза, по сравнению со вторым.
Список литературы:
1.Гаджинский А.М. Логистика: Учеб. пособие — 20-ое изд. — М.: Издательско-торговая корпорация «Дашков и К», 2012. — 484 с.
2.Кобелев Н.Б. Практика применения экономико-математических методов и моделей: Учеб.-практ. пособие — М.: ЗАО «Финстатинформ», 2010. — 246 с.
3.Лукинский В.С. Логистика в примерах и задачах: учеб. пособие / В.С. Лукинский, В.И. Бережной, Е.И. Бережная. — М.: Финансы и статистика, 2009. — 228 с.
4.Плоткин Б.К., Делюкин Л.А. Экономико-математические методы и модели в логистике: Учебное пособие. — СПб.: Изд-во СПбГУЭФ, 2010. — 96 с.
5.Сток Д., Ламберт Д. Стратегическое управление логистикой: Учеб. пособие — перевод с англ. изд. /под ред. Сергеева С.И. —– М.: ИД «Инфра-М», 2008. — 828 с.
дипломов


Комментарии (1)
Оставить комментарий