Статья опубликована в рамках: IX Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 07 марта 2013 г.)
Наука: Математика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
О НЕКОТОРЫХ МЕТОДАХ ЧИСЛЕННОГО РЕШЕНИЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА С ПОСЛЕДУЮЩЕЙ РАЗРАБОТКОЙ ПРОГРАММЫ ДЛЯ ПК
Прокопчук Алексей Николаевич
студент 4 курса факультета естественных наук, математики и технологий
Забайкальского государственного университета, г. Чита
E-mail: alexei.prokopchuk@mail.ru
Беломестнова Вера Ревокатовна
научный руководитель, канд. пед. наук, доцент кафедры фундаментальной и прикладной математики, теории и методики обучения математике Забайкальского государственного университета, г. Чита
Пусть требуется решить дифференциальное уравнение первого порядка
![]() , удовлетворяющее начальному условию
, удовлетворяющее начальному условию ![]() в некотором промежутке
в некотором промежутке ![]() . Для решения уравнения будем пользоваться одним из следующих численных методов.
. Для решения уравнения будем пользоваться одним из следующих численных методов.
Метод Эйлера.
Назовем величину ![]() шагом интегрирования. Эта величина выбирается малой. Метод Эйлера состоит в том, что в коротком промежутке
шагом интегрирования. Эта величина выбирается малой. Метод Эйлера состоит в том, что в коротком промежутке ![]() функцию
функцию ![]() приближенно заменяют постоянной величиной
приближенно заменяют постоянной величиной ![]() , которая определена, если величина
, которая определена, если величина ![]() выбрана, а
выбрана, а ![]() уже определена. Тогда, имеет место равенство:
уже определена. Тогда, имеет место равенство:
![]() (1)
(1)
позволяющее последовательно определять величины ![]() если заданы
если заданы ![]() и
и ![]() и выбраны узлы [3, c. 35].
и выбраны узлы [3, c. 35].
Метод Рунге-Кутта
Пусть ![]() — целое положительное число и
— целое положительное число и ![]() — положительные числа. Пусть числа
— положительные числа. Пусть числа ![]() (
(![]() и
и ![]() удовлетворяют условиям:
удовлетворяют условиям:

![]()

Один этап метода Рунге-Кутта (переход от ![]() к
к ![]() ) таков:
) таков:
1. Вычисляются одно за другим следующие ![]() чисел:
чисел:

2. Вычисляется сумма произведений:
 (3)
(3)
3. Вычисляется ![]() по формуле:
по формуле:
![]()
Числа ![]() при заданном
при заданном ![]() выбираются так, чтобы разность:
выбираются так, чтобы разность:

(![]() решение исходного уравнения, удовлетворяющее условию
решение исходного уравнения, удовлетворяющее условию ![]() ), рассматриваемая как функция переменного
), рассматриваемая как функция переменного ![]() была бесконечно малой возможно более высокого порядка
была бесконечно малой возможно более высокого порядка ![]() относительно
относительно ![]() при
при ![]() .[3, c.36]
.[3, c.36]
Приведем наиболее употребительную систему этих чисел:

Такое прием будем называть соответствующим приемом Рунге-Кутта. Приведем порядок вычислений в этом случае:
1. Вычисляется ![]()
2. Вычисляется 
3. Вычисляется 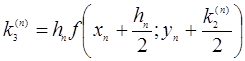
4. Вычисляется ![]()
5. Вычисляется 
6. Вычисляется ![]()
Метод Адамса.
Пусть для дифференциального уравнения ![]() с начальным условием
с начальным условием ![]() найдены каким – либо способом три последовательных значения искомой функции («начальный отрезок»):
найдены каким – либо способом три последовательных значения искомой функции («начальный отрезок»):
![]()
![]()
![]()
С помощью этих значений вычисляют величины:

Записываем значения ![]() таблицу 1 и вычисляем конечные разности величины
таблицу 1 и вычисляем конечные разности величины ![]() (числа над ломаной линей таблицы 1)
(числа над ломаной линей таблицы 1)
Метод Адамса состоит в продолжении этой таблицы разностей с помощью формулы:

которая называется экстраполяционной формулой Адамса. Она применяется для «предсказания» значения ![]() . Подсчитанное по этой формуле «предсказанное» значение мы будем обозначать через
. Подсчитанное по этой формуле «предсказанное» значение мы будем обозначать через ![]() . Полученное по формуле (4) значение
. Полученное по формуле (4) значение ![]() еще нужно уточнить. Для этого нужно написать в таблицу значения
еще нужно уточнить. Для этого нужно написать в таблицу значения ![]() , дополнить таблицу разностей, а затем сделать перерасчет по формуле «коррекции»:
, дополнить таблицу разностей, а затем сделать перерасчет по формуле «коррекции»:
 (5)
(5)
которая называется интерполяционной формулой Адамса. Уточненное с помощью формулы (5) значение мы будем обозначать через ![]() [2, c. 215].
[2, c. 215].
Формулы (4) и (5) имеют достаточно большую точность. Они дают погрешность порядка ![]()
Таблица 1.
Порядок вычислений по методу Адамса

Метод Милна
Пусть для дифференциального уравнения ![]() помимо начального условия
помимо начального условия ![]() известен «начальный отрезок» т. е. значение искомой функции
известен «начальный отрезок» т. е. значение искомой функции ![]() в точках
в точках ![]() (их можно найти одним из методов, изложенных выше). Последующие значения
(их можно найти одним из методов, изложенных выше). Последующие значения ![]() при
при ![]() определяются следующим образом. Для предсказания используется первая формула Милна:
определяются следующим образом. Для предсказания используется первая формула Милна:
 (6)
(6)
Используя ![]() находим
находим ![]() и производим уточнение (коррекцию) по второй формуле Милна:
и производим уточнение (коррекцию) по второй формуле Милна:
 (7)
(7)
Абсолютная погрешность ![]() более точного значения
более точного значения ![]() приближенно определяется по формуле:
приближенно определяется по формуле:
 (8)
(8)
Эта формула позволяет на каждом шаге контролировать точность полученного результата. Если искомое решение требуется найти с точностью до ![]() и окажется, что
и окажется, что ![]() , то можем положить
, то можем положить ![]() и перейти к вычислению
и перейти к вычислению ![]() . В противном случае следует уменьшить шаг
. В противном случае следует уменьшить шаг ![]() [2, c. 224].
[2, c. 224].
Для практического выяснения наиболее точного метода численного решения обыкновенных дифференциальных уравнений первого порядка решим уравнение ![]() с начальным условием
с начальным условием ![]() . Вычислить значение решения этого уравнения при
. Вычислить значение решения этого уравнения при ![]() [1, c. 387].
[1, c. 387].
Вычисления будем вести с четырьмя знаками после запятой. Выберем шаг равный ![]() . Тогда весь участок интегрирования от
. Тогда весь участок интегрирования от ![]() до
до ![]() разобьется на шесть равных частей длиной 0,25 с помощью точек
разобьется на шесть равных частей длиной 0,25 с помощью точек ![]() .
.
Метод Эйлера.
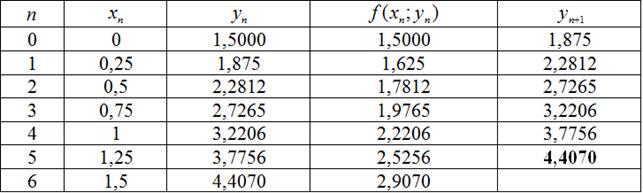
Используя формулу (1) проводим вычисления. Результаты представим в виде таблицы 2.
Таблица 2.
Результаты вычисления методом Эйлера
Метод Рунге-Кутта
Используя соответствующий прием Рунге-Кутта, состоящий из шагов 1—6 (см. выше) проводим вычисления. Результаты представим в таблице 3
Таблица 3.
Результаты вычисления методом Рунге-Кутта

Для того чтобы решить уравнение методом Адамса или методом Милна необходимо знать первые последовательные значения, которые могут быть найдены методом Эйлера или методом Рунге-Кутта. Поэтому, будем решать уравнение методом Адамса и методом Милна, используя сначала первые значения, найденные по методу Эйлера, а затем те значения, найденные по методу Адамса.
Решаем уравнения методом Адамса и методом Милна, используя первые значения, найденные по методу Эйлера. При решении пользуемся формулами Адамса (4) и формулами Милна (6)—(7), выполняя коррекцию по формуле (8). Результаты представим в таблицах 4(метод Адамса) и 5(метод Милна) соответственно.
Таблица 4.
Результаты вычисления методом Адамса

Таблица 5.
Результаты вычисления методом Милна

Решим уравнение методом Адамса и методом Милна, используя в качестве начальных значений, значения вычисленные методом Рунге-Кутта. Результаты представим в таблицах 6 (метод Адамса) и 7 (метод Милна) соответственно.
Таблица 6.
Результаты вычисления методом Адамса

Таблица 7.
Результаты вычисления методом Милна

Окончательно представим результаты вычисления в таблице 8. Здесь ![]() — точное решение уравнения в точке
— точное решение уравнения в точке ![]() ,
,![]() приближенное решении уравнения в точке
приближенное решении уравнения в точке ![]() ,
, ![]() погрешность метода.
погрешность метода.
Таблица 8.
Результаты всех вычислений

Таким образом, наиболее точное численное решение дифференциальных уравнений первого порядка дает комбинация метода РунгеКутта и Милна. Также, достаточно точное численное решение дает и метод РунгеКутта.
Поставим перед собой задачу разработать программу, позволяющую решать дифференциальные уравнения первого порядка. Представим код программ на языке Delphi.
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls;
type
TForm1 = class(TForm)
Label1: TLabel;
Label2: TLabel;
Label3: TLabel;
Label4: TLabel;
Label5: TLabel;
Label6: TLabel;
Label7: TLabel;
Edit1: TEdit;
Edit2: TEdit;
Edit3: TEdit;
Edit4: TEdit;
Button1: TButton;
ListBox1: TListBox;
procedure Button1Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
procedure TForm1.Button1Click(Sender: TObject);
var
i:integer;
a,b,m,h,y,x,y1:real;
k1,k2,k3,k4:real;
function f(x,y:real):real;
begin
f:=y-x; end;
begin
a:=StrToFloat(edit1.Text);
b:=StrToFloat(edit2.Text);
m:=StrToFloat(edit3.Text);
y:=StrToFloat(edit4.Text);
h:=(b-a)/m; y1:=y; i:=1; x:=a;
repeat
k1:=h*f(x,y);
x:=x+h/2;
y:=y1+k1/2;
k2:=h*f(x,y);
y:=y1+k2/2;
k3:=h*f(x,y);
x:=x+h/2;
y:=y1+k3;
k4:=h*f(x,y);
y:=y1+(k1+2*k2+2*k3+k4)/6;
ListBox1.Items.Add(FormatFloat('y(0.#####)=',x)+FormatFloat('0.#####',y));
i:=i+1; y1:=y;
until not (i<=m);
end; end.

Рисунок 1. Интерфейс программы и результаты решения уравнения
Список литературы:
1.Демидович Б.П. Задачи и упражнения по математическому анализу для вузов: учеб. пособие. М.:АСТ: Астрель; Владимир: ВКТ, 2008. — 495 с.
2.Копченова Н.В., Марон И.А. Вычислительная математика в примерах и задачах. М.: Наука.1972. — 368 с.
3.Михлин С.Г., Березин С.Г, Смолицкий Х.Л. Приближенные методы решения дифференциальных и интегральных уравнений. М.: Наука. 1965. — 386 с.
дипломов


Оставить комментарий