Статья опубликована в рамках: V Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 22 октября 2012 г.)
Наука: Технические науки
Секция: Моделирование
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
отправлен участнику
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ОПТИЧЕСКОЙ ЛИНЗЫ ОТРИЦАТЕЛЬНОГО ПРЕЛОМЛЕНИЯ
Сеитбек Даулет Эсмухамедулы
студент 2 курса, кафедра математического и компьютерного моделирования, ВКГТУ, г. Усть-Каменогорск
Е-mail: seitbek_daulet@mail.ru
Гарифуллина Жадыра Рифхатовна
научный руководитель, преподаватель, магистрант тех. наук, кафедра информационные системы, ВКГТУ, г. Усть-Каменогорск
Оптика является одной из областей научного исследования, где эффективно применяется математическое и компьютерное моделирование. Результаты исследования в области оптики в форме оптических приборов, устройств, находятся в большом требовании в почти всех областях деятельности человека.
В научной литературе [6, c. 176; 7, c. 231; 8, c. 211; 9, c. 166; 10, c. 177] рассматриваются собирающие линзы из левого материала, имеющие форму плоскопараллельной пластинки. Но у такой линзы есть недостаток: она фокусирует в одну точку только те лучи, угол падения которых близок к нулю. Все остальные лучи, исходящие из источника, теряются.
Цель работы: найти форму собирающей линзы из материала с отрицательным показателем преломления такую, чтобы она фокусировала в одну точку все лучи, исходящие от точечного источника, при всех углах падения.
Задачи:
1. Изучение хода световых лучей при преломлении на границе обычного вещества и вещества с отрицательным показателем преломлением. Обобщение принципа Ферма для левых сред.
2. Численное моделирование формы поверхности линзы из левого материала, фокусирующей в одну точку все лучи, исходящие от точечного источника.
3. Изучение свойств изображений, полученных в линзе из левого материала.
Изготовление линзы такой специальной формы открывает новые перспективы для развития технологий, что подтверждает актуальность и практическую значимость исследования.
В работе для построения формы линзы из материала с отрицательным показателем преломления, фокусирующей в одну точку все лучи точечного источника, применялся метод численного моделирования с применением языка программирования ФОРТРАН. Результаты обобщались и систематизировались. Для исследования хода лучей в «левых средах» применялись математический анализ и аналитическая геометрия.
Основные результаты:
1. Построен алгоритм и написана программа (на фортране), с помощью которых можно вычислять формы линз из левого материала, собирающей в одну точку все лучи, исходящие от точечного источника, при любом показателе преломления. Пример такой линзы показан на рис. 1.

Рисунок 1. Построение изображения в линзе из вещества с отрицательным показателем преломления п=–3
А — источник, Е — изображение. Синяя линия — поверхность линзы
3. Изучены свойства изображения и оптические свойства поверхности линзы из вещества с отрицательным показателем преломления.
4. В ходе исследования изучен ход лучей при преломлении на границе левых сред и обобщен принцип Ферма.
Все наши результаты новые и могут применяться на практике.
Ключевые слова: Принцип Ферма, суперлинзы, вещества с отрицательным показателем преломления, численное моделирование и язык программирования ФОРТРАН.
ВВЕДЕНИЕ
Оптика — один из старейших разделов физики — переживает в наши дни настоящее возрождение. В последние годы получены материалы со столь необычными оптическими свойствами, что свет в них может замедлиться в триллионы раз, в то время как скорость света в природных материалах замедляется максимум в два с половиной раза. Публикуются даже работы, описывающие принцип создания плаща-невидимки [4].
Поведение луча света зависит от среды, в которой он распространяется. Сейчас уже созданы искусственные среды с отрицательным показателем преломления, в которых свет преломлялся «в неправильную сторону». Поведение света в таких средах предсказал в 1960-е годы советский физик В.Г. Веселаго [1, с. 439].
Явление отрицательного преломления открывает замечательные перспективы для развития технологий. В частности, одной из главных целей исследователей является создание суперлинзы, которая бы фокусировала свет в область размером меньше, чем длина волны света, т. е. лучше, чем это в принципе способны сделать обычные линзы.
Для микроволнового излучения определенной частоты фотонный кристалл, используемый в этом эксперименте, выглядел как среда с отрицательным показателем преломления. Поместив такую пластинку перед источником излучения и просканировав поле позади нее, исследователи убедились, что она действительно фокусирует расходящееся излучение.
Этот впечатляющий эксперимент, демонстрирующий сверхвысокое разрешение линзы, заключался в следующем. Два точечных источника, расположенных на расстоянии 10 мм друг от друга, испускали микроволновое излучение с длиной волны 18 мм. В случае «обычной» линзы изображения от столь близких источников попросту слились бы в одно пятно. Новая же линза выдала изображение двух отдельных четко различимых пятнышек размером около 5 мм. Авторы работы выражают уверенность в том, что усовершенствование их методики в скором времени еще сильнее улучшит свойства суперлинз.
В другой недавней статье американские физики сообщают о создании нового метаматериала, обладающего отрицательным коэффициентом преломления в ближнем инфракрасном диапазоне. Отличие этой работы от предыдущих состоит в том, что типичный размер неоднородностей в этой структуре составляет сотни нанометров, что существенно меньше длины волны инфракрасного света. Из-за этого излучение «чувствует себя» не в решетке (фотонном кристалле), а в почти однородной среде, словно внутри материала совершенно нового типа (именно это и подразумевает слово «метаматериал»). Изюминкой этой работы является эффективная технология выращивания образца достаточно большого размера и микроскопической толщины.
Такие суперлинзы должны привести к прорыву в радио — и оптоэлектронике, оптических устройствах хранения данных, материаловедении, поэтому изучение возможностей, предоставляемых метаматериалами, является актуальной задачей.
Вещества, которые обладают отрицательным показателем преломления, были названы в [9, c. 166; 10, c. 177] “left-handed materials” («левые среды»). В русскоязычной научной литературе также применяется термин, предложенный академиком В.Г. Веселаго, «вещества с отрицательным преломлением» (сокращенно ВОП). Соответственно обычные вещества называют «вещества с положительным преломлением» (или ВПП) [2, c. 129].
В научной литературе рассматриваются собирающие линзы из левого материала, имеющие форму плоскопараллельной пластинки. Но у такой линзы есть недостаток: она фокусирует в одну точку только те лучи, угол падения которых близок к нулю. Все остальные лучи, исходящие из источника, теряются.
Весь набор законов геометрической оптики выводится из принципа экстремума. Но, очевидно, что для новых материалов с отрицательным показателем преломления принцип Ферма, а также основные законы геометрической оптики нуждаются в уточнении.
ЧАСТЬ 1
ОПТИЧЕСКИЕ СВОЙСТВА ЛЕВЫХ СРЕД. ПРИНЦИП ФЕРМА ДЛЯ СРЕД С ОТРИЦАТЕЛЬНЫМ ПОКАЗАТЕЛЕМ ПРЕЛОМЛЕНИЯ
Среды обладают дисперсионными свойствами — волны разных частот распространяются в средах с различными фазовыми скоростями. Это явление называют дисперсией.При распространении монохроматической волны в среде с дисперсией никаких особых явлений не наблюдается; волна распространяется со своей фазовой скоростью, которая определяется значением показателя преломления на частоте волны. Но если в диспергирующей среде одновременно распространяется группа волн разных частот, то по мере распространения волн возникают фазовые сдвиги между отдельными спектральными компонентами. При этом происходит деформация формы суммарного процесса. Если на входе в диспергирующую среду возмущение имело вид импульса (волнового пакета) определенной формы, то после прохождения некоторого слоя форма импульса может существенно измениться.

Рисунок 2. Преломление света на границе двух сред.

Рисунок 3. Прохождение света через плоскую границу двух сред с показателями преломления п1 и п2
Рассмотрим закон, точнее — принцип — принцип Ферма.
Формулировка этого принципа в литературе встречается в разных вариантах. Например:
Луч света всегда распространяется в пространстве между двумя точками по тому пути, вдоль которого время его прохождения меньше, чем вдоль любого другого пути, соединяющего эти точки [5, c. 144].
Проиллюстрируем это на рис. 3, на котором изображены возможные пути луча, пересекающего плоскую поверхность, разделяющую две среды, имеющие показатели преломления п1 и п2.
В том случае, если п1 и п2 оба положительны (т. е. обе среды состоят из ВПП), луч идет по пути АО1В , а углы ![]() и
и ![]() удовлетворяют закону Снеллиуса:
удовлетворяют закону Снеллиуса:
![]() .
.
Оптическая длина этого пути равна:
L=n1· АО1+n2·О1В.
Далее мы докажем, что закон Снеллиуса будет выполняться, если производная оптического пути L будет равна нулю. При этом сама величина L для реального пути будет минимальна и положительна.
Если п1 и п2 оба отрицательны (т. е. обе среды состоят из ВОП), ход лучей будет такой же, как и в предыдущем случае, но с одним важным отличием. В первом случае волновой вектор в обоих средах направлен вдоль лучей, т. е. от А к В, а во втором случае волновой вектор направлен против направления лучей, т. е. от В к А. При этом оптическая длина L оказывается отрицательной и для реального пути АО1В будет максимальной.
Оба случая соответствуют положительному значению величины ![]() относительного показателя преломления второй среды относительно первой.
относительного показателя преломления второй среды относительно первой.
Положение существенно изменится, если величина ![]() будет отрицательной. Это произойдет, если по одну сторону границы находится ВПП, а по другую — ВОП. Тогда луч из первой среды во вторую пойдет по пути АО3В, для углов
будет отрицательной. Это произойдет, если по одну сторону границы находится ВПП, а по другую — ВОП. Тогда луч из первой среды во вторую пойдет по пути АО3В, для углов ![]() и
и ![]() по-прежнему будет выполняться закон Снеллиуса, но с отрицательным значением угла
по-прежнему будет выполняться закон Снеллиуса, но с отрицательным значением угла ![]() .
.
Подчеркнем, что в этом случае реальный путь от точки А до В не является самым коротким по времени распространения. Например, виртуальный путь АО2В свет пройдет за меньшее время, а путь АО4В — за большее время по сравнению со временем прохождения светом реального пути АО3В.
Поэтому формулировка принципа Ферма через время распространения не является корректной.
Для реального пути распространения света будет выполнено условие экстремума оптической длины пути с учетом знака относительного показателя преломления. Рассмотрим доказательство этого факта (рис. 4) для преломления лучей на границе ВПП и ВОП. Пусть сверху снова расположен материал с показателем преломления ![]() , а снизу — материал с показателем преломления
, а снизу — материал с показателем преломления ![]() . Пусть точка А — источник света, точка С — произвольная точка на границе веществ, точка В — некоторая точка преломленного луча.
. Пусть точка А — источник света, точка С — произвольная точка на границе веществ, точка В — некоторая точка преломленного луча.

Рисунок 4. Преломления лучей на границе ВПП и ВОП
Оптическая длина пути АСВ равна:
![]() .
.
Или: ![]() .
.
Найдем первую производную оптической длины пути по переменной х:
 .
.
Очевидно, что производная ![]() равна нулю в том и только в том случае, если выполняется закон Снеллиуса:
равна нулю в том и только в том случае, если выполняется закон Снеллиуса:
![]() =0
=0
с учетом знака показателя преломления ![]() .
.
Отметим, что когда относительный показатель преломления двух сред отрицательный, нельзя заранее утверждать, что экстремум длины оптического пути будет обязательно максимумом или минимумом. Тип экстремума зависит от геометрии конкретной задачи и конкретных величин п1 и п2.
В этом можно убедиться, если найти вторую производную: если она положительна, то имеет место минимум, а если вторая производная отрицательна — то у функции имеется максимум. Найдем вторую производную от длины оптического пути:
 .
.
Последнее выражение может принимать как положительные, так и отрицательные значения или равняться нулю, в зависимости от взаимного расположения точек А, В и С.
Все сказанное позволяет обобщить принцип Ферма для сред с отрицательным показателем преломления.
Мы предлагаем записать принцип Ферма через экстремум длины оптического пути:
Реальный путь распространения света в среде соответствует локальному экстремуму длины оптического пути.
Слово «локальный» указывает на тот факт, что в задаче могут быть несколько возможных оптических путей. Отметим, что в такой формулировке принцип Ферма справедлив и для материалов с положительным показателем преломления.
Длина оптического пути L между точками А и В в общем случае, когда коэффициент преломления меняется от точки к точке, задается интегралом:
![]() .
.
Т. к. величина п, входящая в эту формулу, может быть и отрицательной, то и длина оптического пути может иметь любой знак и любую величину. Если свет проходит через ВОП, то эта длина будет отрицательной.
ЧАСТЬ 2
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ФОРМЫ ПОВЕРХНОСТИ ЛИНЗЫ ИЗ ЛЕВОГО МАТЕРИАЛА
В некоторых случаях длина оптического пути может равняться нулю. Именно такова длина оптического пути между объектом и его изображением в линзе, сделанной из ВОП и изображенной на рис. 5. Здесь изображена плоскопараллельная пластинка из левого материала, которая действует как собирающая линза.
Очевидно, что расстояние от источника до его изображения равно удвоенной толщине пластинки. Если источник расположен на расстоянии от пластинки, превышающем ее толщину, то изображение получится мнимое.
Рассмотрим формирование изображения при преломлении лучей на границе ВПП и ВОП. (рис. 6) Пусть сверху расположен материал с показателем преломления ![]() , а снизу — материал с показателем преломления
, а снизу — материал с показателем преломления ![]() . Пусть точка А — источник света, точка С — произвольная точка на границе веществ, точка В — лежит на продолжении перпендикуляра, опущенного из А на границу раздела.
. Пусть точка А — источник света, точка С — произвольная точка на границе веществ, точка В — лежит на продолжении перпендикуляра, опущенного из А на границу раздела.

Рисунок 5. Прохождение света от объекта А к изображению В сквозь плоскопараллельную линзу, изготовленную из ВОП с коэффициентом преломления ![]() .
.

Рисунок 6. Формирование изображения при преломлении лучей на границе ВПП и ВОП.
Обозначим расстояние от источника до границы ![]() , расстояние от границы до изображения
, расстояние от границы до изображения ![]() .
.
Из закона Снеллиуса:
![]()
следует, что:
![]() , или
, или ![]() .
.
Тогда, ![]() , где относительный показатель преломления равен по модулю:
, где относительный показатель преломления равен по модулю: ![]() . Найдем отношение:
. Найдем отношение:
 ,
,
![]() . (1)
. (1)
Чаще всего теоретически рассматривают ВОП такие, что ![]() , тогда из формулы (1) следует, что
, тогда из формулы (1) следует, что ![]() , все лучи от точечного источника А собираются в точке В, расположенной симметрично относительно границы раздела сред.
, все лучи от точечного источника А собираются в точке В, расположенной симметрично относительно границы раздела сред.
Эту ситуацию иллюстрирует рис 5, на котором в качестве линзы используется плоскопараллельная пластинка из ВОП. Линза из идеальной левой среды (ВОП), у которой ε = μ = –1, создает действительное изображение всех точек предмета, расположенных в слое, ширина которого равна толщине пластины (рис 7).

Рисунок 7. Объемное изображение, получаемое из плоскопараллельной пластины из левого материала.
В работе [8, c. 211] доказано, что разрешающая способность такой плоской линзы превышает предел, обусловленный волновой природой света.
Английский физик Джон Пендри показал, что такая «суперлинза» будет фокусировать свет в точку, размером в сотни раз меньшую, чем длина волны падающего света. В то же время в «правой» оптике, как известно, нельзя получить изображение такого же качества, что и исходное, прошедшее через обычную линзу, т. к. нельзя сфокусировать луч в точку, размерами меньше длины волны (умноженной на константу). Для «левой» оптики такого ограничения не существует!
Как следует из (1), для достаточно малых углов ![]() все лучи, исходящие из точки А, приблизительно пересекаются в точке В для любых
все лучи, исходящие из точки А, приблизительно пересекаются в точке В для любых ![]() . Т. е. и в случае произвольного отрицательного относительного показателя преломления граница раздела правой и левой сред может служить линзой, но только для малых углов падения.
. Т. е. и в случае произвольного отрицательного относительного показателя преломления граница раздела правой и левой сред может служить линзой, но только для малых углов падения.
Если угол ![]() мал, то
мал, то ![]() ,
, ![]() , поэтому из (1) следует, что:
, поэтому из (1) следует, что:
![]() . (2)
. (2)
Действительный график функции расстояния ![]() изображения от границы как функции угла
изображения от границы как функции угла ![]()
![]() падения луча на границу раздела сред для значения
падения луча на границу раздела сред для значения ![]() представлении на рисунке 8. При этом расстояния
представлении на рисунке 8. При этом расстояния ![]() источника мы положили равным
источника мы положили равным ![]() :
:
![]() .
.

Рисунок 8. Действительный график функции расстояния ![]() изображения
изображения

Рисунок 9. Отсутствие изображения, при ![]() значении функции
значении функции ![]()
Как видно из графика, при ![]() значение функции
значение функции ![]() . Изображение при этом не существует, что иллюстрирует рис 9:
. Изображение при этом не существует, что иллюстрирует рис 9:
Для небольших углов падения (приблизительно ![]() ) преломленные лучи практически пересекаются в одной точке. При увеличении угла падения расстояние до пересечения преломленнго луча с прямой АВ резко возрастает, и изображения нет.
) преломленные лучи практически пересекаются в одной точке. При увеличении угла падения расстояние до пересечения преломленнго луча с прямой АВ резко возрастает, и изображения нет.
Чтобы получить изображение для отрицательного значения коэффициента преломления ![]() можно «искривить» поверхность раздела сред на некоторый угол, свой для каждого угла падения. Таким образом, плоская пластинка превратится в некоторую «закругленную» поверхность строго определенной формы.
можно «искривить» поверхность раздела сред на некоторый угол, свой для каждого угла падения. Таким образом, плоская пластинка превратится в некоторую «закругленную» поверхность строго определенной формы.
В нашей работе с помощью численного моделирования решена задача построения такой поверхности раздела сред, для которой все лучи, исходящие из точки А, после преломления пересекутся в одной точке (рис. 10). При этом предполагается, что относительный показатель преломления сред ![]() . В соответствии с формулой (2) расстояние до изображения В равно:
. В соответствии с формулой (2) расстояние до изображения В равно: ![]() или
или
![]() . (3)
. (3)
Здесь АО — перпендикуляр к поверхности, ограниченной отрезком ОС1, угол падения ![]() ,
, ![]() - перпендикуляр к поверхности раздела сред в точке падения луча.
- перпендикуляр к поверхности раздела сред в точке падения луча.
Найдем угол ![]() , на который нужно повернуть поверхность раздела, чтобы преломленный луч пошел по пути
, на который нужно повернуть поверхность раздела, чтобы преломленный луч пошел по пути ![]() .
.
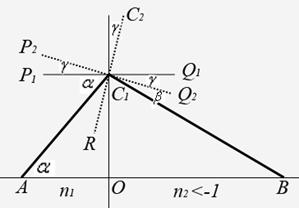
Рисунок 10. Нахождение угла ![]()
На рисунке 10 обозначено: ![]() — положение элемента поверхности после поворота на угол
— положение элемента поверхности после поворота на угол ![]() , отрезок
, отрезок ![]() — нормаль к этой новой поверхности в точке
— нормаль к этой новой поверхности в точке ![]() .
.
Из треугольников АОС1 и ВОС1 получим:
![]() ,
, ![]() ,
,
откуда с учетом (3) следует, что:
![]() . (4)
. (4)
Закон преломления Снеллиуса:
![]() , (5)
, (5)
где угол преломления есть ![]() .
.
Систему уравнений (4), (5) для неизвестных величин ![]() и
и ![]() мы решали численно следующим образом.
мы решали численно следующим образом.
1. Зная координаты точек ![]() и О, с помощью скалярного произведения векторов определяем угол
и О, с помощью скалярного произведения векторов определяем угол ![]() :
:
2. 
3. Рассматриваем последовательные значения угла ![]() такие:
такие: ![]() ,
, ![]() ,
, ![]() — достаточно малый угол (в нашей программе он равнялся
— достаточно малый угол (в нашей программе он равнялся ![]() ). Для каждого
). Для каждого ![]() из уравнения (5) находим угол
из уравнения (5) находим угол ![]() :
:
 . (6)
. (6)
4. В соответствии с уравнением (4) проверяем равенство нулю выражения:
![]() . (7)
. (7)
Если выражение в левой части (7) дает ноль с некоторой заданной точностью (в нашей программе она составила ![]() ), то угол
), то угол ![]() принимается за искомый угол поворота поверхности в точке
принимается за искомый угол поворота поверхности в точке ![]() .
.
Расчеты показали, что выражение в левой части (7) монотонно возрастает: пока угол ![]() мал, оно отрицательно, начиная с некоторого значения
мал, оно отрицательно, начиная с некоторого значения ![]() это выражение становится положительным. Уменьшая интервал, в котором заключен корень уравнения (7), можно определить угол поворота поверхности
это выражение становится положительным. Уменьшая интервал, в котором заключен корень уравнения (7), можно определить угол поворота поверхности ![]() с любой наперед заданной точностью.
с любой наперед заданной точностью.
ЗАКЛЮЧЕНИЕ
Изучая ВОП, мы показали, что обычная формулировка принципа Ферма (через время прохождения луча от источника до изображения) не применима для левых сред. Мы предложили и обосновали обобщенную формулировку этого принципа, верную для любых сред (и правых, и левых): Реальный путь распространения света в среде соответствует локальному экстремуму длины оптического пути.
Теоретически обычно рассматривают левые вещества с относительным показателем преломления ![]() , т. к. это наиболее простой случай, позволяющий изучить основные особенности плоскопараллельной пластинки, выполняющей роль линзы.
, т. к. это наиболее простой случай, позволяющий изучить основные особенности плоскопараллельной пластинки, выполняющей роль линзы.
Практически же изготавливаются метаматериалы с показателем ![]() , для которых до сих пор не были найдены и не объяснены: оптимальная форма линзы, ее свойства, а также свойства получаемого с ее помощью изображения.
, для которых до сих пор не были найдены и не объяснены: оптимальная форма линзы, ее свойства, а также свойства получаемого с ее помощью изображения.
В нашей работе восполняется этот пробел.
В ходе численных экспериментов и программирования на языке FORTRAN мы нашли такую форму линзы из левого материала, которая бы могла давать четкое изображение при значении относительного показателя преломления ![]() .
.
Мы установили свойства этого изображения.
Список литературы:
1.Блиох К.Ю., Блиох Ю.П. Что такое левые среды и чем они интересны? УФН, т. 174, 2004 — 439 с.
2.Веселаго В.Г. УФН 172 (2002) — 129 c.
3.Жувикин Г. Лабиринты фотонных кристаллов. — Журнал «Компьютера» 2001, № 30 — 231 c.
4.Иванова И. Материалы с сайта — [Электронный ресурс] — Режим доступа — URL: http://elementy.ru/news/430422 — октярбрь 2009 года.
5.Физический энциклопедический словарь. — М.: Сов Энциклопедия, 1983 — 144 c.
6.Fang N. et al., Science, 308, 534 (22 April 2005) — 176 c.
7.Lu Zh. Et al., Physical Review Letters, 95, 153901 (4 October 2005) — 231 c.
8.Pendry J.B. Negative refraction makes a perfect lens. Phys. Rev. Letters. 85 3966 (2000) — 211 c.
9.Shelby R.A., Smith D.R., Schultz S. Science 292—77 (2001) — 166 c.
10.Smith D.R. et al. Phys. Rev. Lett. 84—4184 (2000) — 177 c.
отправлен участнику


Комментарии (4)
Оставить комментарий