ОПЕРАЦИОННЫЙ  МЕТОД  РЕШЕНИЯ  ЛИНЕЙНЫХ  ДИФФЕРЕНЦИАЛЬНЫХ  УРАВНЕНИЙ  И  ИХ  СИСТЕМ

Жгилев  Данил  Юрьевич

студент  2  курса,  факультет  электроэнергетики  и  электротехники  ДВФУ,  г.  Владивосток

E-mail:  danil-gw@mail.ru

Дмух  Галина  Юрьевна

научный  руководитель,  канд.  пед.  наук,  доцент  кафедры  алгебры,  геометрии  и  анализа,  ДВФУ,  г.  Владивосток

Операционный  метод  приобрел  большое  значение  при  решении  линейных  дифференциальных  уравнений  с  постоянными  коэффициентами.  Эффективность  применения  операционного  исчисления  при  решении  линейных  обыкновенных  дифференциальных  уравнений  состоит  в  удобстве  и  простоте  вычислений.  Прежде  всего  это  относится  к  решению  систем  таких  уравнений  [4,  с.  131].

Рассмотрим  обыкновенное  дифференциальное  уравнение  n-го  порядка  с  постоянными  коэффициентами

  (1)

где  коэффициенты  -постоянные  величины,  при  начальных  условиях 

x(0)=  ,  (0)  ,  ...  ,  (0)=  (2)

где  —  заданные  числа  [3,  с.  126].

Операционный  метод  решения  состоит  в  том,  что  мы  считаем  как  искомую  функцию  x(t),  так  и  правую  часть  f(t)  оригиналами  и  переходим  от  уравнения  (1)  ,  связывающего  оригиналы,  к  уравнению,  связывающему  их  изображения  X(p)  и  F(p),  тогда  x(t)≑X(p),  а  f(t)≑F(p).  Воспользуемся  теоремой  о  дифференцировании  оригинала:

,

.......

,

Применяя  свойство  линейности  получаем  вместо  уравнения  (1)  алгебраическое  соотношение,  которое  назовем  изображением,  или  операторным  уравнением:

++...+()+  [2,  с.  127—128]

В  результате  мы  получили  уже  не  дифференциальное,  а  алгебраическое  уравнение  относительно  неизвестного  изображения  X(p). 

где    ,

-алгебраические  многочлены  от  p  степени  n  и  n-1  соответственно  [1,  с.  264].

Из  последнего  уравнения  находим

  (3)

Полученное  равенство  называют  операторным  решением  дифференциального  уравнения  (1).  Остается  по  полученному  изображению  X(p)  найти  оригинал  x(t)  ,  применяя  для  этого  соответствующие  правила  операционного  исчисления.  Найденный  оригинал  x(t)  будет  являться  частным  решением  дифференциального  уравнения  (1)  [3,  с.  128].

Пример:  найдем  решение  дифференциального  уравнения  операционным  методом    при  условиях 

Решение: 

пусть  x(t)≑X(p)=X.  Тогда 

=

Подставим  эти  выражения  в  дифференциальное  уравнение,  получим  операторное  уравнение:    .  Отсюда  X(p)=

Для  нахождения  оригинала  разложим  дробь  на  простейшие

A(p+1)+B(p-3)(p+1)+C=1

Ap+A+B-2Bp-3B+C-6Cp+9С=1

Составим  систему  уравнений:

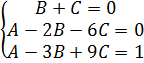
Решив  ее,  получаем

Итак  X(p)=  ,  откуда 

x(t)=—  решение  данного  дифференциального  уравнения.

Системы  линейных  дифференциальных  уравнений  с  постоянными  коэффициентами  можно  решать  операционными  методами  совершенно  так  же,  как  и  отдельные  уравнения;  все  отличие  заключается  лишь  в  том,  что  вместо  одного  изображающего  уравнения  приходим  к  системе  таких  уравнений,  причем  система  эта  в  отношении  изображений  искомых  функций  будет  линейно  алгебраической.  При  этом  никаких  предварительных  преобразований  исходной  системы  дифференциальных  уравнений  производить  не  требуется  [3,  с.  134].

Метод  решения  таких  систем  покажем  на  примере.

Пример:  решить  систему  дифференциальных  уравнений

при  начальных  условиях  x(0)=2  ,  y(0)=0.

Решение: 

пусть  x(t)≑X(p)=X,  y(t)≑Y(p)=Y.  Тогда

Подставим  эти  выражения  в  систему  дифференциальных  уравнений,  система  операторных  уравнений  принимает  вид:

Решая  эту  систему  уже  алгебраических  уравнений  ,  находим:

X(p)=  ,

Y(p)=

Раскладывая  найденные  изображения  на  простые  дроби  находим:

X(p)=  ,

Y(p)=  .

Переходя  от  изображений  к  оригиналам,  получаем  искомые  решения:

x(t)=

y(t)=.

Таким  образом  операционный  метод  позволяет  в  ряде  случаев  значительно  упростить  процедуру  нахождения  решения  линейных  дифференциальных  уравнений  и  их  систем.

Список  литературы:

1.Араманович  И.Г.,  Лунц  Г.Л.,  Эльсгольц  Л.Э.  Функции  комплексного  переменного.  Операционное  исчисление.  Теория  устойчивости.  -М.,  Главная  редакция  физико-математической  литературы,  1968  г.,  —  стр.  416.  —  Избранные  главы  высшей  математики  для  инженеров  и  студентов  втузов.  —  263—268  с.

2.Диткин  В.А.,  Прудников  А.П.  Интегральные  преобразования  и  операционное  исчисление.  М.:  Физматгиз,  1961.  —  127—132  с.

3.Шостак  Р.Я.  Операционное  исчисление.  Краткий  курс.  Изд.  второе,  доп.Учебное  пособие  для  вузов  М.  «Высшая  школа»,  1972  —  126—139  с.

4.Штокало  И.3.  Операционное  исчисление  (обобщения  и  приложения)  Киев,  Издательство  «Наукова  Думка»,  1972  —131—144  с.