Статья опубликована в рамках: XX Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 15 мая 2014 г.)
Наука: Математика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ГЕОМЕТРИЧЕСКИЙ ОБРАЗ ЧЕТЫРЁХМЕРНОГО ШАРА.
Егоров Нестер Александрович
студент 4 курса, кафедра алгебры и геометрии ИМИ СВФУ, РФ, г. Якутск
E -mail: egrvnester@mail.ru
Попов Олег Николаевич
научный руководитель, канд. техн. наук, доцент ИМИ СВФУ, РФ, г. Якутск
В настоящей работе дается представление четырехмерного шара в четырехмерном пространстве с помощью его трехмерных сечений. Для объяснения трудностей, связанных с восприятием объектов четырёхмерного пространства, используется метод, который основан на рассмотрении пространств с более низкой размерностью. Актуальность данного подхода заключается в том, что он позволяет понять строение геометрических образов четырехмерного пространства, а также способствует развитию пространственного и абстрактного мышления. Данная работа представляет интерес для учащихся старших классов, студентов факультетов математических и естественных наук, а также учителей математики. Она излагается наглядным методом, без использования формул, на основе лишь школьного курса геометрии.
В научной и популярной литературе, в средствах массовой информации, часто упоминаются многомерные пространства и объекты. Существуют различные теории о многомерности нашей Вселенной. Человеку свойственно геометрические объекты представлять в наглядной форме. Поэтому многие, услышав словосочетание «четырёхмерный шар», сразу же пытаются наглядно представить его в своём воображении. Мы хорошо представляем двумерный шар (это круг, лежащий на плоскости), трёхмерный шар — объект, который часто встречается в нашей жизни. Но в четырёхмерном случае, мы никак не можем построить в нашем воображении геометрический образ четырёхмерного шара. Это связано с появлением четвёртого, недоступного для нас, измерения.
Формирование на интуитивном уровне понятного читателю представления о геометрическом образе четырёхмерного шара является целью нашей работы. В ней не используются строгие определения, математические формулы. Все используемые понятия, термины понимаются только интуитивно. Весь материал излагается в популярной форме.
Актуальность работы состоит в том, что она позволяет понять строение геометрических образов четырехмерного пространства, а также способствует развитию пространственного и абстрактного мышления и представляет интерес для учащихся старших классов, студентов факультетов математических и естественных наук, а также учителей математики.

Рисунок 1. а) Прямая четырехмерном пространстве пересекает трехмерный шар только в одной внутренней точке; б) Прямая на плоскости пересекает двумерный шар по отрезку; в) Прямая, расположенная в пространстве, пересекает двумерный шар только в одной точке
Четырехмерное пространство в некоторой степени является необычным пространством. Мы знаем, что в трёхмерном пространстве прямая линия пересекает ограниченный трёхмерный выпуклый объём (например, шар) по отрезку. Исключение составляет случай, когда прямая линия касается данного объекта. В четырехмерном пространстве всё может происходить иначе. Прямая линия может «пронзить» трёхмерный шар насквозь, задев только одну внутреннюю точку, не потревожив её окружение (рис. 1, а)). Это делает возможным для четырёхмерного человека (если бы он существовал) забрать все наши вещи из сумки, не раскрывая и не разрезая её, что кажется очень необычным и необъяснимым. Чтобы понять это, рассмотрим двумерное пространство (двумерное пространство — это плоскость, вложенная в трёхмерное пространство). Прямая на плоскости будет пересекать круг, расположенный в плоскости по отрезку, а прямая пространства, лежащая вне плоскости, пересечёт круг только в одной точке (рис. 1, б), с)).
Чтобы эпизод пропажи вещей из сумки был более понятным, нарисуем на доске двумерного человека, нарисуем его почки, камень в почке. Затем возьмём в руки тряпку и аккуратно, не задевая почки двумерного человека, сотрём камень (рис. 2). Теперь можем поздравить самого себя с тем, что мы только что успешно произвели операцию по удалению камня из почки без использования разрезов, и что наш пациент здоров. То, что неподвластно двумерному хирургу, оказалось простым делом для обычного трёхмерного человека.

Рисунок 2. Удаление камня из двумерной почки трехмерным доктором без резервов
Далее мы будем пользоваться данным приемом, связанным с переходом на размерность ниже для объяснения трудностей, связанных с восприятием объектов, находящихся в четырёхмерном пространстве. Трудности восприятия двумерного человека, когда он пытается понять трёхмерный мир, аналогичны нашим при восприятии четырёхмерного пространства, так как они связаны в обоих случаях появлением нового недоступного измерения.
Два трёхмерных пространства могут пересекаться или быть параллельными в четырёхмерном пространстве. Рассмотрим случай, когда они пересекаются.

Рисунок 3. Два трехмерных пространства пересекаются в четырехмерном пространстве по плоскости
Если две плоскости x и y пересекаются по прямой l (рис. 4), то трёхмерные пространства P и Q пересекаются по плоскости α (рис. 3). Для двумерного человека прямая l (если она непрозрачна) будет стеной, разделившей его мир на две части. А полуплоскости y1 и y2 для него не существуют, так как находятся в недоступном для него, третьем измерении. Для трёхмерного человека такой стеной, разбивающей всё пространство на две части, будет плоскость α (рис. 3).
Далее, рассмотрим две пересекающиеся плоскости x и y, по одной из которых катится двумерный мяч (рис. 4). Заметим, что двумерный человек видит только прямую l из плоскости y, так как она находится в его пространстве x. Полуплоскости y1 и y2 ему невидимы, поэтому двумерный человек, находящийся в плоскости x увидит точку (плоский мяч коснулся прямой), которая затем раздвоится (мяч пересёк прямую). Далее, по мере движения мяча, точки будут расходиться, пока прямая пересечения плоскостей не совпадет с диаметром мяча, затем всё будет происходить в обратном порядке.

Рисунок 4. Двумерный человек видит только точку касания круга с его плоскостью
Теперь нетрудно понять, что мы увидим, находясь в трёхмерном пространстве P, в случае, когда мяч, запущенный ногой футболиста, находящегося в Q, пересечёт наше пространство. Вначале на плоскости α. появится точка, которая сразу же преобразуется в постепенно увеличивающуюся окружность, являющуюся пересечением плоскости α и мяча. Достигнув своего максимума, при радиусе равном радиусу футбольного мяча, она постепенно начнет уменьшаться до тех пор, пока не выродится обратно в точку и исчезнет с поля зрения (рис. 5). Что же мы увидим, когда вслед за мячом пробежит сам футболист, оставим вообразить читателю. Для интереса же представим, что произойдет, если футболист, каким-то невероятным способом, находясь в пространстве Q, случайно свернёт в наше пространство P (см. рис. 6).

Рисунок 5. Вид мяча, пересекшего пространство наблюдателя, в динамике

Рисунок 6. Пявление футболста в пространстве P из пространства Q
В двумерном варианте легко представить две параллельные плоскости. Трёхмерное пространство можно представить как бесконечную совокупность параллельных «слипшихся» плоскостей. Такое представление можно получить, глядя на колоду карт, где каждая карта ассоциируется с плоскостью или книгой, где роль плоскостей выполняют листы данной книги.
Четырёхмерное пространство тоже представляет совокупность «слипшихся», но уже трехмерных параллельных пространств. Попытайтесь представить в своём воображении два параллельных (слипшихся), т. е. расположенных очень близко друг к другу, трёхмерных пространства. У вас ничего не получится. Пространства, которые мы хотим представить в своём воображении, либо начинают пересекаться, либо не хотят сближаться, отталкиваясь друг от друга. Разберёмся в причине нашей неудачи. Для этого проанализируем, как попытается представить двумерный человек, живущий в плоскости x, две очень близко лежащие друг к другу параллельные плоскости y и z. Так как для двумерного человека не существует третьего измерения h (рис. 7а)), то он будет вынужден расположить их в своем пространстве, хотя в реальности они будут располагаться перпендикулярно (или под некоторым углом) пересекая плоскость x (рис. 7б)). Теперь сразу же становится очевидным, в чём состоит причина нашей неудачи. Мы пытаемся поместить два трёхмерных пространства в одно трехмерное пространство, в котором находимся (рис. 7с)), когда же они должны простираться по четвёртому, недоступному нам измерению. Понятно, что они никак не смогут казаться слипшимися.
Заметим, что трёхмерное пространство можно представить как след, оставляемый плоскостью в результате её движения по заданному направлению (рис. 8).

Рисунок 7. а) Двумерный человек пытается представить две параллельные плоскости; б) Реальное расположение параллеьных плоскостей; с) Мы пытаемя поместить два трехмерных пространства в одно тремерное пространство
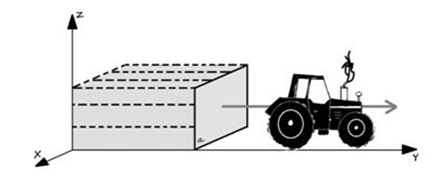
Рисунок 8. Трехмерное пространство, получаемое движением плоскости
Теперь, как и ранее, рассмотрим пространства P и Q, пересекающиеся по плоскости α (рис. 9а)). Каждое из пространств можно получить движением плоскости α соответственно направлениям осей координат x и t. Далее проведём в пространстве P плоскость β на очень близком расстоянии параллельно плоскости α. Очевидно, β не будет находиться в пространстве Q. Начнём движение данных плоскостей по направлению t так, что в любой момент t движущиеся плоскости были параллельны и близки друг к другу. Тогда пространство Q и пространство Qβ, полученные движением соответственно плоскостей α и β, параллельны, и будут находиться на очень близком расстоянии друг от друга (на расстоянии, равном расстоянию между плоскостями α и β, по измерению x). Тогда два трёхмерных тела, например, два шара, находящиеся в совершенно разных, но близких друг к другу параллельных пространствах Q и Qβ, могут оказаться очень близкими («слипшимися») (рис. 9б)).

Рисунок 9. а) Плоскость β из лоскости P близка и параллельна плоскости α и не находится в пространстве Q; б) Совокупности плоскостей, полученных движением плоскостей α и β по направлению t, образуют близкие друг к другу араллельные пространства Q и Qβ Изображенныешары, находящиеся в этихх пространствах, близки друг к другу по всем точкам(«слипшиеся» шары)
Всё четырёхмерное пространство можно рассматривать как совокупность параллельных, очень близко расположенных («слипшихся») трёхмерных пространств. Если в качестве четвёртого измерения взять время, то движение человека на машине времени будет соответствовать переходу из одного параллельного пространства в другое. В этом случае, в отличие от пересекающихся пространств, когда мы видим только сечение объекта, который движется по второму пространству, пересекая наше, перед нами неожиданно возникнет машина времени с сидящим в ней человеком, которая растворится в прошлом или будущем в зависимости от направления её движения.
Таким образом: мы поняли, что трёхмерные пространства пересекаются по плоскости; четырёхмерное пространство можно представить как совокупность «слипшихся» параллельных трёхмерных пространств; получили представление о «слипшихся» трёхмерных телах, находящихся в параллельных пространствах.
Что собой представляет собой четырехмерный шар? Чтобы ответить на этот вопрос проанализируем то, как устроен наш обычный трёхмерный шар, с точки зрения двумерного человека. Безусловно, полностью шар он видеть не может, в его поле зрения находится только двумерная сфера — окружность, окаймляющая двумерный круг, и являющаяся пересечением мира двумерного человека с шаром (то, что находится внутри окружности, ему не видно. Рис10 а)). При переходе в параллельные пространства окружность будет сужаться, пока не выродится в точку (рис. 10 б)).

Рисунок 10. а) Двумерному человеку видна только часть окружности, окаймляющая пересчением плоскости и шара; б) При переходе человека в параллельные плоскости окржность постепенно выродится в точку
В случае четырёхмерного шара, поле зрения человека ограничено пространством, в котором он находится. По аналогии можно предположить, что он видит сферу, окаймляющую шар, являющуюся пересечением данного трёхмерного пространства с четырёхмерным шаром. При переходе в параллельные пространства сфера также будет уменьшаться в радиусе, пока не выродится в точку (рис. 11 а)). Теперь постараемся более подробно разобраться, что за шары мы видим, и как они образуют четырёхмерный шар.
Рассмотрим трёхмерный шар 2 (рис. 11 б)) и его сечения параллельными плоскостями. Совокупность этих параллельных плоскостей образуют трёхмерное пространство с измерениями y, z, t, в котором находится искомый шар 2. Каждая из этих плоскостей своим движением по направлению x образуют «слипшиеся» трёхмерные пространства. Именно в этих пространствах находятся трёхмерные шары (см. шар 1), которые мы наблюдаем при (описанных выше) переходах в параллельные пространства (рис. 11а)). Совокупность данных шаров будет образовывать четырёхмерный шар. Таким образом, четырёхмерный шар есть совокупность слипающихся по всем точкам шаров, уменьшающихся в размерах, которая и образует геометрический образ четырёхмерного шара. Однако мы не можем увидеть общую цельную картину шара, так как не можем видеть вне нашего пространства.

Рисунок 11. а) Видимые человеком, при переходах в параллельные пространства шары, уменьшающихся в размерах; б) Четырехмерный шар представляет собой совокупность уменьшающихся «слившихся» шаров, являющихся сечениями четырехмерного шара трехмерными пространствами, параллельными пространству P
Рассмотрим четырёхмерный шар с разных сторон. Наблюдатель, находящийся в трехмерном пространстве P с измерениями y, z, t и смотрящий по направлению t, будет видеть шар (рис. 12), который состоит из сечений шаров, образующих четырёхмерный шар (на рис. 11 это шар 2).
Наблюдатель, находящийся в пространстве Q и смотрящий по направлению x, так же увидит трёхмерный шар (рис 12). Таким образом, наблюдатели, находящиеся в пространствах P и Q, видят одну и ту же картинку — трёхмерный шар. Однако шары, которые они наблюдают, являются различными геометрическими объектами, находящимися в различных пространствах и пересекающимися по двумерному кругу.

Рисунок 12. Наблюдатели, находящиеся в пересекающихся пространствах P и Q видят трехмерный шар. Однако на самом деле они обозревают различные шары, пересекающиеся по кугу
К нашему сожалению, как было отмечено выше, поле нашего зрения ограничивается трёхмерным пространством, поэтому мы не можем видеть четырёхмерные образы в целом. Тем не менее, британский математик Ч. Хинтон (1853—1907) разработал особый метод построения моделей геометрических фигур в четырехмерном пространстве по их трехмерным сечениям. Этот метод подробно изложен в двух его монографиях [1, с. 49], [2, с. 42]. Хинтон утверждал, что в результате многолетней работы, в основе которой лежал этот особый метод, он научился мысленно представлять геометрические образы в четырёхмерном пространстве. Он также полагал, что человек, достаточно хорошо овладевший этим методом, обретет интуитивное представление о четырёхмерном пространстве.
Список литературы:
1.Hinton Charles H. A New Era of Thought, orig. 1888, reprinted 1900, by Swan Sonnenschein & Co. Ltd., London — с. 240.
2.Hinton Charles H. The Fourth Dimension, orig. 1904, 1912 by Ayer Co., Kessinger Press reprint, ISBN 0-405-07953-2, scanned version available online at the Internet Archive — с. 170.
дипломов


Оставить комментарий