Статья опубликована в рамках: XXVI Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 18 ноября 2014 г.)
Наука: Математика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
КОНТАКТНОЕ ВЗАИМОДЕЙСТВИЕ ДВУХ ЦИЛИНДРИЧЕСКИХ ПЛАСТИН
Филиппова Наталья Олеговна
студент 4 курса, кафедра математического моделирования и кибернетики СыктГУ, РФ, г. Сыктывкар
E-mail : nataljafilipp5@gmail.com
Ермоленко Андрей Васильевич
научный руководитель, канд. физ.-мат. наук, доцент СыктГУ, РФ, г. Сыктывкар
Рассмотрим следующую контактную задачу со свободной границей. Две пластины толщины ![]() и ширины
и ширины ![]() , расположены параллельно друг другу с зазором
, расположены параллельно друг другу с зазором ![]() . Верхняя пластина находится под действием нормальной нагрузки
. Верхняя пластина находится под действием нормальной нагрузки ![]() . При этом на краях пластин
. При этом на краях пластин ![]() выполняются условия жесткого закрепления, края
выполняются условия жесткого закрепления, края ![]() закреплены шарнирно, а два других края бесконечно удалены или загружены так, что в пластинах реализуется цилиндрический изгиб. Под действием определенной нагрузки первая пластина коснется второй, в результате чего вторая пластина также начнет изгибаться. Предположим, что область контакта
закреплены шарнирно, а два других края бесконечно удалены или загружены так, что в пластинах реализуется цилиндрический изгиб. Под действием определенной нагрузки первая пластина коснется второй, в результате чего вторая пластина также начнет изгибаться. Предположим, что область контакта ![]() двух пластин является непрерывной. Требуется определить прогибы пластин и возникающие контактные реакции.
двух пластин является непрерывной. Требуется определить прогибы пластин и возникающие контактные реакции.
Для решения поставленной задачи воспользуемся уравнением Софи Жермен–Лагранжа, см., например [3]. Данное уравнение имеет следующий вид:
|
|
|
(1) |
Здесь w — прогиб пластины (т. е. перемещение по нормали), ![]() — нормальная нагрузка,
— нормальная нагрузка, ![]() — действующие на верхнюю и нижнюю лицевые поверхности пластины нагрузки,
— действующие на верхнюю и нижнюю лицевые поверхности пластины нагрузки,  — цилиндрическая жесткость, h — толщина пластины, E и n — модуль Юнга и коэффициент Пуассона,
— цилиндрическая жесткость, h — толщина пластины, E и n — модуль Юнга и коэффициент Пуассона,  — оператор Лапласа в декартовых координатах.
— оператор Лапласа в декартовых координатах.
В случае цилиндрического изгиба  , поэтому уравнение (1) примет вид
, поэтому уравнение (1) примет вид
|
|
|
(2) |
Таким образом, для первой пластины получаем уравнение
|
|
|
(3) |
для второй —
|
|
|
(4) |
Здесь ![]() — активная нагрузка, действующая на верхнюю пластину,
— активная нагрузка, действующая на верхнюю пластину, ![]() — реакция со стороны второй пластины на первую. В свою очередь
— реакция со стороны второй пластины на первую. В свою очередь ![]() является нагрузкой, с которой первая пластина давит на вторую.
является нагрузкой, с которой первая пластина давит на вторую.
Граничные условия пластин имеют вид
|
|
|
(5) |
Здесь соотношения (5)1 – условия жесткого закрепления, (5)2 — условия шарнирного закрепления.
Рассмотрим ![]() Тогда в соответствии с принципом суперпозиции решения [4] имеем
Тогда в соответствии с принципом суперпозиции решения [4] имеем
|
|
|
(6) |
Для удобства обозначим ![]() через
через ![]() , тогда выражение (6) перепишется следующим образом:
, тогда выражение (6) перепишется следующим образом:
|
|
|
(7) |
Граничные условия запишутся следующим образом:
|
|
|
(8) |
В соответствии с подходом статей [1; 5] решение краевой задачи {(7), (8)} будем искать с использованием функции Грина
|
|
|
(9) |
|
|
|
|
||
Здесь  — функция Хевисайда.
— функция Хевисайда.
Далее прогиб рассматривается на отрезке ![]() . В этом случае он принимает вид
. В этом случае он принимает вид
|
|
|
(10) |
Подставив выражение (10) в (7), получаем, что ![]() при
при ![]()
Учитывая, что на лицевые поверхности пластины действует два вида нагрузок: активная ![]() и реактивная
и реактивная ![]() получаем, что
получаем, что
|
|
|
(11) |
Тогда общее выражение для реакции имеет вид
|
|
|
(12) |
где ![]() — сосредоточенные реакции на границе области контакта.
— сосредоточенные реакции на границе области контакта.
Используя соотношение (12), нормальная нагрузка ![]() записывается в виде
записывается в виде
|
|
|
(13) |
Используя функцию Грина (9), решение краевой задачи {(7), (8)} с правой частью в виде (13) имеет вид
|
|
|
|
|
|
|
(14) |
Прогиб ![]() при
при ![]() записывается в виде
записывается в виде
|
|
|
(15) |
Отметим, что выражения (10) и (15) должны совпадать при ![]() Поэтому приравнивая в правых частях выражений (10) и (15) коэффициенты при одинаковых степенях
Поэтому приравнивая в правых частях выражений (10) и (15) коэффициенты при одинаковых степенях ![]() получим следующие уравнения:
получим следующие уравнения:
|
|
|
|
|
|
|
(16) |
Решение системы (16) можно записать в виде
|
|
|
(17)
(18) |
Отметим, что выражения для ![]() согласуются с полученными в статьях [2; 5].
согласуются с полученными в статьях [2; 5].
Используя полученные значения (17), (18) исходные уравнения для прогибов пластин запишутся следующим образом:
|
|
|
(19) |
|
|
|
(20) |
В качестве примера на рисунке 1 приведены графики прогибов пластин со следующими физическими и геометрическими параметрами:
· для рис. 1а:
|
|
|
(21) |
· для рис.1б:
|
|
|
(22) |


а б
Рисунок 1. Графики прогибов: ----- ![]() - - -
- - - ![]()
Значения граничных точек зоны контакта и сосредоточенные реакции при параметрах (21) будут равны
|
|
|
(23) |
при параметрах (22):
|
|
|
(24) |
Список литературы:
1.Ермоленко А.В. Аналитическое решение контактной задачи для жестко закрепленной пластины и основания. В мире научных открытий. Красноярск: НИЦ, 2011. — С. 11—17.
2.Михайловский Е.И., Бадокин К.В., Ермоленко А.В. Теория изгиба пластин типа Кармана без гипотез Кирхгофа // Вестник Сыктывкарского универси-тета. Сер. 1: Мат. Мех. Инф. — 1999. — Вып. 3. — С. 181—202.
3. Михайловский Е.И., Торопов А.В. Математические модели теории упругости. Сыктывкар: Сыктывкарский ун-т, 1995. — 251 с.
4.Тихонов А.Н., Самарский А.А. Уравнения математической физики. М.: Изд-во МГУ, 1999.
5.Филиппова Н.О. Об одной контактной задаче для цилиндрической пластины // Сборник материалов Международной научно-практической конференции «Теоретические и прикладные проблемы технических и математических наук». Украина. Киев. — 2014. — № 4. — С. 39—42.
дипломов








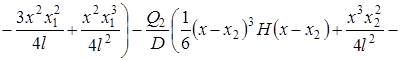










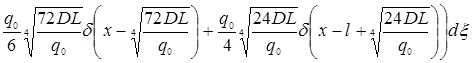

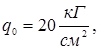
Оставить комментарий