ГЕОМЕТРИЧЕСКИЕ  ОБРАЗЫ  ПОВЕРХНОСТЕЙ  ВРАЩЕНИЯ  В  ЧЕТЫРЕХМЕРНОМ  ПРОСТРАНСТВЕ

Егоров  Нестер  Александрович

студент  4  курса,  кафедра  алгебры  и  геометрии  ИМИ  СВФУ,  РФ,  г.  Якутск

E -mail:  egrvnester@mail.ru

Попов  Олег  Николаевич

научный  руководитель,  канд.  техн.  наук,  доцент  ИМИ  СВФУ,  РФ,  г.  Якутск

Как  известно,  в  трёхмерном  пространстве  круговой  цилиндр  можно  получить  вращением  прямой  L  параллельной  некоторой  оси  вокруг  этой  оси  (рис.  1).  Уравнение  цилиндра  задается  в  виде    для  любого  значения  z.  Заметим,  что  в  направляющей  кругового  цилиндра  является  окружность  (одномерная  сфера).

Рисунок  1.  Вращение  прямой  L   вокруг  оси  z

«При  этом  вращении  прямой  L,  каждая  её  точка  N  вращается  вокруг  соответствующей  точки  N₁  оси  z,  образуя  окружность.  Семейство  полученных  таким  образом  окружностей  зависит  от  параметра  z  и  является  искомым  цилиндром»  [1,  с.  122].

«Проведём  аналогичное  вращение,  поднявшись  на  размерность  выше,  вращая  плоскость  α,  расположенную  в  пространстве  Otyz,  x=0  (аналог  прямой  L)  вокруг  координатной  плоскости  β  Otz,  y=0,  x=0  (аналог  оси  z)  в  четырёхмерном  пространстве  (рис.  1,  рис.  2).  Из  рисунка  2  видно,  что  прямые  l₁  и  l₂,  лежащие  на  плоскости  α  перпендикулярно  координатной  плоскости  Oyt,  x=0,  z=0  вращаются  соответственно  вокруг  прямых  m₁  и  m₂,  расположенных  на  плоскости  Otz,  y=0,  x=0»  [2,  с.  33].

При  этом  прямая  l₁  своим  вращением  образует  цилиндр  в  пространстве  Oxyz,  t=0,  уравнение  которого  имеет  вид  .

Очевидно,  любая  прямая  плоскости  α,  параллельная  l₁,  вращаясь  вокруг  своей  оси,  также  порождает  двумерную  поверхность  —  цилиндр  в  трёхмерном  пространстве.

Рисунок  2.  Вращение  плоскости  α  вокруг  плоскости  β

Совокупность  всех  прямых  данной  плоскости,  параллельных  l₁,  будут  порождать  семейство  двумерных  цилиндров  с  параметром  t,  образующее  трёхмерную  поверхность  в  четырёхмерном  пространстве  Oxyzt.  Уравнением  цилиндра  данного  семейства  при  фиксированном  значении  t=t₀  является

Отпуская  параметр  t  с  фиксированного  значения  t₀,  получим  уравнение    (1).

Данное  уравнение  описывает  геометрический  образ  трёхмерной  поверхности,  полученной  вращением  плоскости  α  вокруг  плоскости  β,  в  четырёхмерном  пространстве.

Рассмотрим  прямую  n,  которая  является  пересечением  α  с  плоскостью  Oyt,  x=0,  z=0.

Проанализируем,  как  вращается  произвольно  взятая  точка  N  на  рассматриваемой  прямой  при  вращении  плоскости  α  вокруг  координатной  плоскости  β.  Из  рисунка  2  видно,  что  точка  N  описывает  окружность  вокруг  оси  Oz,  располагаясь  в  плоскости  Oxy,  z=0,  t=0.

Однако  точка  N  также  вращается  и  вокруг  оси  Ot,  так  как  данная  ось  также  перпендикулярна  плоскости  окружности  и  пересекает  эту  плоскость  в  той  же  точке,  что  и  ось  Oz  (рис.  4).  Это  означает,  что  прямая  n  вращается  вокруг  оси  Ot  (так  как  вокруг  оси  Ot  вращается  каждая  её  точка).  При  этом  в  пространстве  Oxyt,  z=0  образуется  двумерный  круговой  цилиндр  Ц  (рис.  3),  который  является  направляющей  поверхностью  цилиндра  (1),  полученного  вращением  плоскости  α  вокруг  плоскости  β  (рис.  3,  рис.  5).  Уравнение  этого  цилиндра  имеет  вид 

Заметим,  что  при  вращении  отрезка  вокруг  оси  получается  цилиндр,  в  основании  которого  находится  окружность,  т.  е.  одномерная  сфера.  «В  случае  вращения  прямоугольника  с  двумя  бесконечными  противоположными  сторонами  вокруг  плоскости  образуется  трёхмерный  цилиндр,  в  основании  которого  находится  двумерный  цилиндр»  [3,  с.  235]. 

Рисунок  3.  Круговой  цилиндр  Ц,  полученный  вращением  плоскости  α  вокруг  плоскости  β

Рисунок  4.  Точка  Q   одновременно  вращается  вокруг  оси  Oz  и  Ot

Рассмотрим  на  рис.  5  как  вращается  плоскость  α  вокруг  плоскости  β.  На  рисунке  видно,  что  каждая  прямая  плоскости  α,  параллельная  оси  Oz  описывает  цилиндр.  Совокупность  вращений  всех  этих  прямых  создаёт  вращение  плоскости  α  вокруг  β  и  при  этом  создаётся  иллюзия  прохождения  α  сквозь  плоскость  β  (хотя  во  время  вращения  плоскостине  должны  пересекаться).

Рисунок  5.  Вращение  плоскости  α  вокруг  плоскости  β

Зададимся  вопросом.  Возникнет  ли  у  двумерного  человека  подобная  иллюзия  при  его  попытке  наглядно  представить  вращение  прямой  относительно  другой  прямой  в  трёхмерном  пространстве?

Пусть  плоскость  α  является  пространством  двумерного  человека  и  параллельные  прямые  σ  и  σ₁  расположены  в  этой  плоскости.  При  вращении  прямой  σ  вокруг  σ₁  каждая  точка  N  прямой  σ  движется  по  окружности,  расположенной  в  трёхмерном  пространстве  (рис.  6,  б)).  Жизненное  пространство  двумерного  человека  ограничено  плоскостью  α.  Поэтому  пытаясь  представить  окружности,  получаемые  движением  точек  σ,  он  вынужден  расположить  их  в  своей  плоскости  (рис.  6,  а)).  В  результате  у  него  прямая  σ  как  совокупность  вращающихся  точек  будет  двигаться  в  плоскости  α.  При  этом  неизбежно  возникнет  иллюзия  того,  что  вращаемая  прямая  при  своём  движении  проходит  через  ось  σ₁.  В  действительности  же  прямая  σ,  движется  вне  плоскости  по  третьему  измерению,  образуя  круговой  цилиндр.  Также  и  в  четырёхмерном  пространстве  мы  вынуждены  представлять  движение  плоскости  в  том  же  пространстве,  где  находимся  сами.  В  реальности  при  вращении  плоскость,  выйдя  из  нашего  пространства,  движется  по  четвертому  измерению.

Рисунок  6.  а)  Двумерный  человек,  пытаясь  представить  окружности,  получаемые  движением  точек  σ,  он  вынужден  расположить  их  в  плоскости;  б)  При  вращении  прямой  σ  вокруг  σ₁  каждая  точка  N   прямой  σ  движется  по  окружности,  расположенной  в  трёхмерном  пространстве

Приведём  рассуждения  логически  объясняющие,  почему  плоскости  α  и  β  не  пересекаются  при  рассматриваемом  вращении  на  рисунке  5.  Пусть  параллельные  пространства  P  и  Q  получены  движением  плоскостей  p  и  q  (рис  7,  а)).  Далее  рассмотрим  на  рисунке  7,  б)  трёхмерный  цилиндр,  получаемый  вращением  плоскости  α  (α  проходит  через  прямые  l₁,  l₂)  вокруг  плоскости  β  (β  проходит  через  прямые  m₁,  m₂).  При  данном  вращении  каждая  точка  прямой  l₁  вращается  вокруг  оси  m₁  в  пространстве  P=Oxyz.  Плоскость  β  пересекается  с  пространством  P  только  по  прямой  m₁  (рис.  7,  б)).  Поэтому  прямая  l₁  при  своём  вращении  не  пересекает  плоскость  β.  Точно  также  прямая  l₂,  вращаясь  вокруг  прямой  m₂  в  пространстве  Q,  не  будет  пересекать  плоскость  β.  Проделанные  рассуждения  можно  распространить  и  на  остальные  прямые,  лежащие  на  плоскости  α  параллельно  прямым  l₁,  l₂.  Следовательно,  плоскость  α  не  пересекает  плоскость  β.

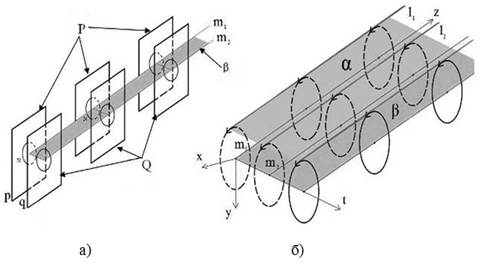
Рисунок  7.  а)  Параллельные  пространства  P   и  Q  получены  движением  плоскостей  p  и  q;  б)  Трёхмерный  цилиндр,  получаемый  вращением  плоскости  α  вокруг  плоскости  β

Далее  мы  будем  рассматривать  геометрические  объекты,  получаемые  вращением  одномерных  кривых  вокруг  плоскости  в  четырёхмерном  пространстве.  Рассмотрим  вращение  кривой  p  (рис.  8).  Сразу  понять,  что  представляет  собой  поверхность  вращения  данной  кривой  достаточно  сложно.  Однако  оказывается,  что  знание  строения  цилиндра  (рис.  5),  получаемого  вращением  одной  плоскости  вокруг  другой  в  четырёхмерном  пространстве,  позволяет  достаточно  просто  представить  геометрические  образы  вращения  кривых  вокруг  некоторой  плоскости.

Точка  N,  лежащая  на  кривой  p  (рис.  8,  рис.  9)  будет  описывать  окружность,  которая  является  направляющей  цилиндра  Ц,  расположенного  в  пространстве  Oxyz,  t=0  ввиду  того,  что  точка  N  лежит  на  прямой  l,  вращение  которой  образует  цилиндр  Ц.  Нетрудно  понять,  что  остальные  точки  кривой  также  будут  описывать  окружности  в  пространствах  Oxyz  при  различных  значениях  t.  Совокупность  этих  окружностей  определяет  трубчатую  двумерную  поверхность  в  четырёхмерном  пространстве  с  образующей  кривой  p.  Сечениями  этой  поверхности  пространствами  Oxyz,  будут  пары  рассмотренных  окружностей.  Проекция  данной  поверхности  на  координатное  пространство  Oxyz,  t=0  представляет  собой  двумерный  цилиндр  Ц  (рис.  9).  На  рисунках  10,  11  и  12  представлены  одномерные  геометрические  объекты  и  их  поверхности  вращения.  Рис.  10  и  рис.  11:  а)  отрезки;  б)  поверхности  вращения  —  «шайба»  и  усечённый  конус.  Рис.  12:  а)  два  взаимно  перпендикулярных  пересекающихся  отрезка  —  «крест»;  б)  поверхность  вращения  —  два  пересекающихся  цилиндра,  лежащие  в  двух  взаимно  перпендикулярных  пространствах.

Рисунок  8 .  Вращение  кривой  p

Рисунок  9.  Проекция  поверхности  на  координатное  пространство  представляет  двумерный  цилиндр  Ц

Рисунок  10.  а)  Одномерный  геометрический  объект  —  отрезок;  б)  Поверхность  вращения  —  «шайба»

Рисунок  11.  а)  Одномерный  геометрический  объект  —  отрезок;  б)  Поверхность  вращения  —  усечённый  конус

Рисунок  12.  а)  Одномерный  геометрический  объект  —  два  взаимно  перпендикулярных  пересекающихся  отрезка  —  «крест»;  б)  Поверхность  вращения  —  два  пересекающихся  цилиндра,  лежащие  в  двух  взаимно  перпендикулярных  пространствах

  Заключение:  разработан  метод,  на  интуитивном  уровне  формирующий  представление  о  геометрических  образах  поверхностей  вращения  в  четырехмерном  пространстве.

Список  литературы:

1.Александров  А.Д.,  Нецветаев  Н.Ю.  Геометрия:  учеб.  пособие.  М.:  Наука.  Гл.  ред.  физ.-мат.  лит.,  1990.  —  672  с.

2.Баишева  М.И.,  Кутукова  Л.Т.  Тезисы  XI  Республиканской  научно-методической  конференции,  посвященной  90-летию  В.В.  Алексеева  и  80-летию  Т.Н.  Селляховой.  Якутск:  ИД  СВФУ,  2014.  —  56  с.

3.Гриб  Е.Н.,  Гриб  Н.Н.,  Павлов  С.С.  Материалы  XIV  Всероссийской  научно-практической  конференции  молодых  ученых,  аспирантов  и  студентов  в  г.  Нерюнгри,  с  международным  участием.  Том  2.  Нерюнгри:  Печатный  Двор,  2013  —  436  с.