Статья опубликована в рамках: XXXV Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 27 октября 2015 г.)
Наука: Математика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ПРАВИЛЬНЫЕ МНОГОГРАННИКИ В ИЗОБРАЗИТЕЛЬНОМ ИСКУССТВЕ
Родина Кристина Сергеевна
студент 2 курса, специальность Фармация, ГБОУ СПО «ПМК» Минздрава России,
РФ, г. Пенза
Казакова Ольга Анатольевна
научный руководитель, преподаватель математики высшей категории, ГБОУ СПО «ПМК» Минздрава России,
РФ, г. Пенза
E-mail: kandincki@mail.ru
В данной работе речь пойдёт об использовании правильных многогранников в изобразительном искусстве.
Разве не приходилось нам ловить себя на том, что мы иногда непроизвольно рисуем какие-то геометрические фигуры, линии? Но было трудно предположить, что правильные многогранники найдут место в художественном искусстве. Однако одной из самых частых тем изобразительного искусства оказалось использование многогранников.
Главной целью работы является развитие Математической культуры. Ведь каждый из нас должен обладать определенным уровнем математической образованности, эрудицией и грамотностью. В данном случае ведется речь не только о познании точной науки, но и о расширении кругозора, стремлении узнать больше. Такой жизненный подход необходим в современном, постоянно развивающемся, мире, полном инноваций.
При этом хочется обратить внимание на то, под каким углом я смотрю на математику, как, сквозь призму точной науки, я пытаюсь открыть необычайно красочный мир. Также в своей работе я стремилась к тому, что бы каждый не просто почерпнул интересные сведения о правильных многогранниках, но еще и почувствовал глубину и глобальность моих рассуждений.
Напомню — правильный многогранник — это выпуклый многогранник, у которого все грани равные правильные многоугольники и из каждой вершины выходит одинаковое количество ребер.
Доказано, что существует только пять правильных многогранников: тетраэдр, куб (гексаэдр), октаэдр, икосаэдр, додекаэдр.
Еще с давних времён можно было отметить большой интерес человека к правильным многогранникам. Например, некоторые древние учёные (Пифагор, Платон) считали, что огонь имеет форму тетраэдра, вода — икосаэдра, Земля — куба, воздух — октаэдра, а вся Вселенная — это додекаэдр.
Правильные многогранники очень распространённые геометрические тела в окружающем нас мире. Множество живых организмов, химических элементов и минералов, которые мы можем встретить в природе, имеют форму правильных многогранников.
Исторически, математика играла важную роль в изобразительном искусстве. Согласно современным взглядам, математика и изобразительное искусство — очень удаленные друг от друга дисциплины. Первая — аналитическая, главную роль в которой играет точность и правильность решения. Вторая — эмоциональная, опирающаяся на чувства и душевное состояние личности. Казалось бы, что между этими сферами не может быть даже малейшего взаимодействия. Но в противопоставление этому хочется обратиться к работам некоторых известных художников, которые своим творчеством доказали притяжение противоположностей и воссоединили два противостоящих друг другу мира — мир математики и мир искусства.
Многие художники разных эпох и стран особо интересовались изучением многогранников, что оставило яркий след в их творчестве. Пик этого интереса приходится, конечно, на эпоху Возрождения.
Изучая явления природы, художники эпохи Возрождения стремились найти опирающиеся на опыт науки способы их изображения. Учения о перспективе, светотени и пропорциях, построенные на математике, оптике, анатомии, становятся основой нового искусства. Они позволяют художникам воссоздавать на плоскости трехмерное пространство, добиваться впечатления рельефности предметов.
Леонардо да Винчи (1452—1519) — титан Возрождения, живописец, скульптор, ученый — увлекался теорией многогранников и часто изображал их на своих полотнах. Он изобрел способ пространственного изображения многогранников называемого сегодня методом жестких ребер и сплошных граней (рис. 1).
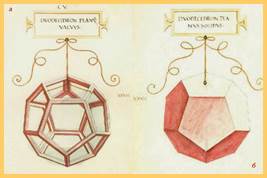
Рисунок 1. а) метод жестких ребер; б) метод сплошных граней
Эта техника впоследствии многократно использовалась художниками, скульпторами и учеными.
Для некоторых мастеров эпохи Возрождения многогранники являлись просто удобной моделью для тренировки мастерства перспективы. Другие восхищались их симметрией и лаконичной красотой. Третьих, вслед за Платоном, привлекали их философские и мистические символы. Таким примером является одна из наиболее таинственных работ Альбрехта Дюрера (1471—1528) — немецкого живописца и графика — резцовая гравюра на меди «Меланхолия» (рис. 2).

Рисунок 2. «Меланхолия»
Замысел «Меланхолии» до сих пор не раскрыт, но образ могучей крылатой женщины впечатляет значительностью, психологической глубиной. Эта картина принадлежит к числу произведений, «повергших в изумление весь мир». Одни, взглянув на неё, погружаются в круговорот собственных предположений о значении каждого изображённого на ней предмета, а другие приобретают такой же задумчивый вид, какой имеет женщина на картине.
Для меня эта картина стала самой запоминающейся. Не смотря на странное сочетание предметов, она заворожила меня своим скрытым жизненным эффектом. Изображённый на ней образ задумчивой девушки, в моём воображении, символизирует людей, но не всех сразу, а каждого по-отдельности. Предметы, окружающие эту девушку — повседневные жизненные проблемы и ситуации, с которыми сталкивается человек в течение дня. И все эти предметы расположены в каком-то беспорядке, как поток мыслей человека. Этот поток не имеет какой-либо последовательности и наполняет чашу человеческого разума до самого верха. Среди этих предметов, всех этих мыслей, событий и ситуаций, человек один, и он никак не может от этого отвлечься и выбраться из этого хаоса. Но, что самое интересное, среди этого беспорядка, художник изобразил правильный многогранник. Он как бы замаскировался на этой картине, предавая ей ещё большую необыкновенность. Возможно, это геометрическое тело (так как оно правильное) обозначает какой-нибудь верный или правильный жизненный путь, выход из этого потока мыслей или решение какой-нибудь жизненной проблемы, причём верное решение. Правильный многогранник позволяет упорядочить все предметы картины и придает ей своеобразное спокойствие.
Нельзя не привести примеры изображений многогранников, выполненных художниками XX века.
Мауриц Корнелис Эшер (1898—1972) — голландский художник, в некотором роде является отцом математического искусства. Правильные многогранники имели особое очарование для Эшера. В его многих работах многогранники являются главной фигурой и в еще большем количестве работ они встречаются в качестве вспомогательных элементов.

Рисунок 3. «Рептилии»
Гравюры Эшера образуют своего рода художественно-геометрический фильм, дающий зрителю редкую возможность увидеть геометрическое начало во многих явлениях природы и красоту — в чисто геометрических конструкциях и построениях. В гравюре «Рептилии» (рис. 3) маленькие крокодилы играючи вырываются из тюрьмы двухмерного пространства стола, проходят кругом, чтобы снова превратиться в двухмерные фигуры. Они находятся в окружении совершенно неожиданных предметов, среди которых есть и правильный многогранник. Я вижу в этой картине жизненный цикл человека: выход из двухмерного пространства стола — рождение, движение по книге, многограннику и другим предметам — обучение, развитие, становление личности, а повторное превращение в двухмерное изображение — смерть. Я считаю, что двигаясь по всем этим предметам человек ищет своё место в мире, своё предназначение, которым и является правильный многогранник.
Изящный пример звездчатого додекаэдра можно найти в работе «Порядок и хаос» (рис. 4). В данном случае звездчатый многогранник помещен внутрь стеклянной сферы. Красота этой конструкции контрастирует с беспорядочно разбросанным по столу мусором. Заметим также, что анализируя картину, можно догадаться о природе источника света для всей композиции — это окно, которое отражается в левой верхней части сферы. Если поразмыслить и связать эту картину с реальным миром, то становится ясно, что хотел сказать художник. Для меня этот многогранник — человек, который знает и видит свой жизненный смысл, ищет и находит свой путь, именно поэтому он так сияет, потому что он одержим идеей и стремлением, потому что он особенный!

Рисунок 4. «Порядок и хаос»
Кроме того, графические фантазии Эшера вовлекают зрителя в противопоставление иллюзии и реальности.
Во многих работах Эшера можно встретить фигуры, полученные объединением правильных многогранников. В работе «Двойной планетоид» (рис. 5) Эшер использовал тетраэдры. Здесь он попытался изобразить параллельный мир (иллюзию) — реальность, существующую каким-то образом одновременно с нашей, но независимо от неё.

Рисунок 5. «Двойной планитоид»
Наиболее интересной среди них является гравюра «Звезды» (рис. 6), на которой можно увидеть тела, полученные объединением тетраэдров, кубов и октаэдров. Если бы Эшер изобразил в данной работе, лишь различные варианты многогранников, мы никогда бы не узнали о ней. Но он по какой-то причине поместил внутрь центральной фигуры хамелеонов, чтобы затруднить нам восприятие всей фигуры. Таким образом, нам необходимо отвлечься от привычного восприятия картины и попытаться взглянуть на нее свежим взором, чтобы представить ее целиком. Этот аспект данной картины является еще одним предметом восхищения математиков творчеством Эшера.

Рисунок 6. «Звезды»
Сальвадор Дали (1904—1989) — яркий и парадоксальный испанский художник использовал математические идеи в некоторых своих картинах.
На картине «Тайная Вечеря» (рис. 7) изображён Христос со своими учениками. Все они облачены в белые одежды, так как белый цвет символизирует чистоту души, честность и искренность. Посмотрев на картину, можно заметить, что они находятся на верхнем этаже здания, что напрямую связанно с величием происходящего собрания. Фон картины — огромный прозрачный додекаэдр. Вы помните, что форму додекаэдра, по мнению древних, имела Вселенная, т. е. они считали, что мы живём внутри свода, имеющего форму поверхности правильного додекаэдра. На картине видно, что при изображении додекаэдра художник использовал технику жестких ребер. Но на самом верху картины также есть ещё один важный элемент: тело человека с разведёнными в стороны руками. Его руки как бы охватывают все предметы и всех присутствующих на этом собрании, оберегая и защищая их. Скорее всего, так художник изобразил Бога. Возможно он хотел, чтобы мы обратили внимание на то, что всё в мире находится под Его воздействием и контролем, а сама Вселенная не является додекаэдром, а только ограничена им, так как именно внутри него мы связанны с Всевышними силами и находимся под их нерушимой защитой.

Рисунок 7. «Тайная Вечеря»
Заключение
Не смотря на разнообразие подходов художников к правильным многогранникам, главное остаётся неизменным: они оставили яркий след в творчестве великих мастеров.
Как известно, изобразительное искусство появилось с самых древних времен, как способ выразить и передать информацию другим людям. Художники в своих работах не просто передают информацию, но еще и дают свою собственную оценку этой информации. Сочетая математические основы с художественным мастерством, им удается вовлечь нас в восприятие многогранников не как объектов геометрии, а как объектов искусства.
Каждый из нас может рассказать о картине по своему, найти в ней то, что, в сущности, беспокоит наше сердце и ответить на многие вопросы, на которые до сих пор кто-то не находил ответов, а также задуматься об истинном смысле казалось бы простых вещей.
Список литературы:
- Волошинов А.В. Математика и искусство. — М.: Просвещение, 1992. — 336 с.
- Глейзер Г.И. История математики в школе. IX—X классы. Пособие для учителей. — М.: Просвещение, 1983. — 351 с.
- Мир математики: в 40 т. Т. 1: Фернандо Корбалан. Золотое сечение. Математический язык красоты. — М.: Де Агостини, 2014. — 160 с.
- Мир математики: в 40 т. Т. 23: Клауди Альсина. Тысяча граней геометрической красоты. Многогранники. — М.: Де Агостини, 2014. — 148 с.
- Смирнова И.М. В мире многогранников: кн. для учащихся. — М.: Просвещение, 1995. — 144 с.
дипломов


Оставить комментарий