Статья опубликована в рамках: XLII Международной научно-практической конференции «Инновации в науке» (Россия, г. Новосибирск, 25 февраля 2015 г.)
Наука: Математика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
ДОКАЗАТЕЛЬСТВО СУЩЕСТВОВАНИЯ РЕШЕНИЯ ИНТЕГРАЛЬНОГО УРАВНЕНИЯ ВОЛЬТЕРРА С ФУНКЦИЕЙ ЛЕЖАНДРА В ЯДРЕ
Вагапов Винер Зуфарович
канд. физ.-мат. наук, доцент Стерлитамакского филиала Башкирского государственного университета, РФ, Республика Башкортостан, г. Стерлитамак
THE PROOF OF EXISTENCE OF THE SOLUTION OF THE INTEGRAL EQUATION OF VOLTERRA WITH THE FUNCTION OF LEGENDRE IN THE KERNEL
Viner Vagapov
candidate of Physical and Mathematical Sciences, associate professor of Sterlitamak branch of Bashkir State University, Russia, Republic of Bashkortostan, Sterlitamak
АННОТАЦИЯ
Статья посвящена доказательству существования решения интегрального уравнения Вольтерра первого рода с функцией Лежандра в ядре.
ABSTRACT
Article is devoted to the proof of existence of solution of Volterra integral equation of the first kind with the function of Legendre in the kernel.
Ключевые слова: интегральное уравнение Вольтерра; функция Лежандра в ядре.
Keywords: Volterra integral equation; function of Legendre in the kernel.
В работе [2] было доказана единственность решения интегрального уравнения

где ![]() ,
, ![]() — функция Лежандра [1, гл. 3]. Используя связь между функциями Лежандра и гипергеометрической функцией Гаусса [1, гл. 2], уравнение (1) было сведено к уравнению
— функция Лежандра [1, гл. 3]. Используя связь между функциями Лежандра и гипергеометрической функцией Гаусса [1, гл. 2], уравнение (1) было сведено к уравнению

где ![]() ,
, ![]() . Воздействуя на уравнение (2) специально подобранным интегральным оператором, была получена формула
. Воздействуя на уравнение (2) специально подобранным интегральным оператором, была получена формула
![]()
![]()

![]()
где ![]() — гипергеометрическая функция двух переменных, введенная профессором В.Ф. Волкодавовым [3].
— гипергеометрическая функция двух переменных, введенная профессором В.Ф. Волкодавовым [3].
Тем самым была доказана единственность решения уравнения (1). Перейдем к доказательству существования решения уравнения (1). Для этого подставим функцию ![]() , определяемую формулой (3), в левую часть уравнения (2). Получим
, определяемую формулой (3), в левую часть уравнения (2). Получим
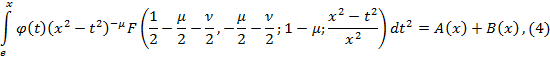
где

![]()
![]()


![]()
В выражении для ![]() функцию Гаусса разложим в степенной ряд по
функцию Гаусса разложим в степенной ряд по ![]() , а функцию
, а функцию![]() —
— ![]() и
и ![]() и поменяем порядок интегрирования и суммирований, будем иметь
и поменяем порядок интегрирования и суммирований, будем иметь



Вычислим последний интеграл с помощью подстановки ![]() и запишем выражение для
и запишем выражение для ![]() в виде
в виде

![]()
После применения к функции Гаусса формулы Больца (4) [1, п. 2.9] получим


Разложим полученную функцию Гаусса в степенной ряд по k, поменяем порядки суммирований и воспользуемся представлением функции ![]() в виде суммы двойного ряда (6) [1, п. 5.7]:
в виде суммы двойного ряда (6) [1, п. 5.7]:

![]()
К функции ![]() применим формулу вырождения (11) [1, п. 5.10] и учтем, что
применим формулу вырождения (11) [1, п. 5.10] и учтем, что ![]() Тогда в силу формулы (4) [1, п. 2.8] окончательно
Тогда в силу формулы (4) [1, п. 2.8] окончательно

Приступим к вычислению ![]() . В повторном интеграле изменим порядок интегрирования, разложим гипергеометрические функции в степенные ряды и поменяем порядки интегрирования и суммирований. После вычисления получившегося внутреннего интеграла с помощью замены переменной
. В повторном интеграле изменим порядок интегрирования, разложим гипергеометрические функции в степенные ряды и поменяем порядки интегрирования и суммирований. После вычисления получившегося внутреннего интеграла с помощью замены переменной ![]() имеем
имеем


![]()
К функции Гаусса применим формулу Больца (4) [1, п. 2.9], полученную функцию Гаусса разложим в степенной ряд по n и поменяем порядки суммирований:

![]()
Учитывая формулу (11) [1, п. 5.10] и то, что ![]() , получаем
, получаем

или в силу формулы (4) [1, п. 2.8] окончательно имеем
![]()
С учетом найденного выражение для ![]() становится следующим:
становится следующим:

Подставляя (5) и (6) в правую часть равенства (4), убеждаемся, что функция (3) действительно обращает уравнение (2) в тождество.
Возвращаясь в (3) к первоначальным обозначениям, получаем формулу обращения для интегрального уравнения (1):
![]()
![]()

![]()
Список литературы:
1.Бейтмен Г., Эрдейи А. Высшие трансцендентные функции. Т. 1. Гипергеометрическая функция. Функции Лежандра. М.: Наука, 1973. — 295 с.
2.Вагапов В.З. Доказательство единственности решения интегрального уравнения Вольтерра с функцией Лежандра в ядре // «Современная наука: актуальные проблемы и их решения»: сборник научных статей XIV Международной научной конференции. Липецк: ООО «Максимал информационные технологии», 2015. — С. 6—12.
3.Волкодавов В.Ф., Николаев Н.Я. Об одной специальной функции двух аргументов, встречающейся при решении краевых задач // Аналитические методы решения дифференциальных уравнений. Куйбышев: Куйбыш. гос. ун-т, 1986. — С. 42—46.
дипломов


Оставить комментарий