УСТОЙЧИВОСТЬ  ПЛОСКОГО ОДНОРОДНОГО  НЕЙРОННОГО  ПОЛЯ

Иванов  Сергей  Александрович

аспирант  кафедры  математического  анализа  Челябинского  государственного  педагогического  университета  (ЧГПУ),  г.  Челябинск

E-mail:  ivanovlord@yandex.ru

Пархоменко  Алексей  Александрович

магистрант,  ЧГПУ,  г.  Челябинск

STABILITY  OF  SIMILAR  FIELD NEURAL  NETWORKS

Ivanov  Sergey

post-graduate  student,  Dept.  of  Mathematical  Analysis, 

Chelyabinsk  State  Pedagogical  University  (CSPU)

Alexey  Parhomenko 

graduate  student,  Dept.  of  Computer  Science  (CSPU)

Работа  поддержана  грантом  Министерства  образования  и  науки  1.1711.2011  и  грантом  для  аспирантов  Челябинского  государственного  педагогического  университета.  Авторы  благодарны  проф.  Кипнису  М.М.  за  постановку  задачи  и  ценные  советы.

АННОТАЦИЯ

Экспериментально  получены  области  устойчивости  дискретных  нейронных  сетей  с  топологией  связей  в  виде  плоского  однородного  поля  в  пространстве  параметров.  Задача  сводится  к  проблеме  устойчивости  матричных  разностных  уравнений  высоких  порядков  с  запаздыванием. 

ABSTRACT

The  stability  domains  of  a  discrete  neural  network  are  obtained  by  numerical  experiments.  The  network  has  similar  field  architecture.  The  problem  is  reduced  to  the  matrix  delay  equations  of  higher  order. 

Ключевые  слова:  нейронные  сети;  разностные  матричные  уравнения;  устойчивость  разностных  уравнений;  нейронные  сети  в  виде  поля.

Keywords:  neural  networks;  difference  matrix  equations;  stability;  similar  field.

Нейрон  является  сложным,  имеет  свои  составляющие,  подсис­темы  и  механизмы  управления  и  передает  информацию  через  большое  количество  электрохимических  связей.  Направление  связи  от  одного  нейрона  к  другому  является  важным  аспектом  нейронных  сетей.  Искусственные  нейронные  сети  являются  электронными  моделями  нейронной  структуры  мозга,  который,  главным  образом,  учится  на  опыте.  Естественный  аналог  доказывает,  что  множество  проблем,  не  поддающиеся  решению  традиционными  компьютерами,  могут  быть  эффективно  решены  с  помощью  нейронных  сетей.

Искусственные  нейронные  сети  (сети  Хопфилда,  1984)  с    нейронами  в  дискретном  линеаризованном  варианте  описываются  разностными  уравнениями

                                                              (1)

Мы  рассматриваем  нейронную  сеть  из  девяти  нейронов  с  архитектурой  связей  в  виде  однородного  поля.

Рисунок  1.  Нейронная  сеть  с  девятью  нейронами  в  виде  поля

В  модели  взаимодействие  различных  нейронов  запаздывает  на  тактов.  Для  сетей  с  архитектурой  связей  в  виде  однородного  поля  уравнение  (1)  примет  вид:

                                                               (2)

где:    —  единичная  матрица  размером  , 

  —  коэффициент  затухания  собственных  колебаний  нейрона, 

—  матрица  взаимодействий  между  нейронами  в  сети.  Здесь    есть  мерный  вектор  состояния  нейронной  сети  в  момент  .

Силу  воздействия  нейрона  на  «левого»  и  «правого»  соседа  обозначим  ,  силу  воздействия  нейрона  на  соседа  «сверху»  и  «снизу»  —  .

Матрица  взаимодействий    размера    примет  вид

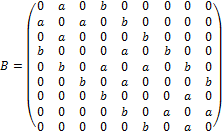.                                                              (3)

Для  численных  экспериментов  нам  понадобится  характерис­тическое  уравнение  для  матричного  уравнения  (2),  которое  имеет  вид

                                         (4) 

где: 

                                    (5)

Для  изучения  устойчивости  уравнения  (2)  с  матрицей  (3)  будем  использовать  программу  MatchcadPrime  2.0.  Зафиксируем  коэффи­циент  собственных  колебаний  ,  запаздывание  .  После  чего  перебираем  значения    из  некоторого  интервала  с  некоторым  шагом.  Для  каждого  выбранного  нами  значения  мы  подбираем  такие  значения  ,  в  окрестности  которых  устойчивость  системы  граничит  с  неустойчивостью.  Мы  ищем  корни  уравнения  (4)  с  учетом  (5).  Искомые  значения    берем  такие,  что  все  корни  характеристического  уравнения  (4)  находятся  внутри  единичного  круга  на  комплексной  плоскости,  а  по  крайней  мере  один  корень  на  границе  круга.  В  результате  мы  получаем  область  устойчивости  в  пространстве  параметров  .  В  конце  создаем  график,  иллюстрирующий  полученную  область  устойчивости  для  выбранных  параметров    и  .

Результаты  вычислений  области  устойчивости  для  значений  запаздывания    показаны  на  Рис.  2.

Рисунок  2.  Области  устойчивости  в  пространстве  параметров  (a,b)  для  γ=0,5,  k=1,  2,  3

Нами  выявлена  следующая  закономерность.  В  области  одновре­менно  положительных    и  ,  как  и  в  области  одновременно  отрицательных    и  ,  граница  устойчивости  от  запаздывания  не  зависит.  В  области  одновременно  положительного    и  отрицательного  ,  как  и  в  области  одновременно  отрицательного    и  положительного    видна  зависимость  от  запаздывания.  При  увели­чении  запаздывания    граница  устойчивости  расположенная  во  второй  и  четвертой  координатных  четвертях  сжимается  к  осям    и  .

Полученные  результаты  подтверждают  теорию  рассмотренную  в  работе  [4]  для  достаточно  больших  нейронных  сетей. 

Рекурсивные  нейронные  сети  с  топологией  связей,  отличной  от  однородного  поля,  изучены  в  работах  [2,  4].  Непрерывные  модели  нейронных  сетей  исследуются  в  работе  [5]  на  основе  теории  конусов  устойчивости  для  дифференциальных  уравнений  с  запаздываниями  [6]. 

Список  литературы:

1.Заенцов  И.В.,  Нейронные  сети:  основные  модели.  Издательство  Воронежского  университета,  Воронеж,  1999.

2.Иванов  С.А.  Область  устойчивости  в  пространстве  параметров  рекур­сивных  нейронных  сетей  с  топологией  многомерного  куба.  Челябинск:  Вестник  ЮУрГУ  серия  Математика.  Механика.  Физика  Выпуск  7,  2012.

3.Кипнис  М.М.,  Нигматулин  Р.М.  Устойчивость  трехчленных  линейных  разностных  уравнений  с  двумя  запаздываниями.  М:  Автоматика  и  телемеханика  №11,  2004.

4.Ivanov  S.A.,  Kipnis  M.M.  Stability  analysis  of  discrete-time  neural  networks  with  delayed  interactions:  torus,  ring,  grid,  line.  International  Journal  of  Pure  and  Applied  Math.  (2012)  V.  78(5),  p.  691—709.

5.Khokhlova  T.N.,  Kipnis  M.M.  Numerical  and  qualitative  stability  analysis  of  ring  and  linear  neural  networks  with  a  large  number  of  neurons,  International  Journal  of  Pure  and  Applied  Math.  (2012)  V.  76(3),  pp.  403—419.

6.Khokhlova  T.N.,  Kipnis  M.M.,  Malygina  V.V.  The  stability  cone  for  a  delay  differential  matrix  equation,  Appl.  Math.Letters  (2011)  V.  24,  pp.  742—745.