Статья опубликована в рамках: III Международной научно-практической конференции «Физико-математические науки и информационные технологии: проблемы и тенденции развития» (Россия, г. Новосибирск, 11 июня 2012 г.)
Наука: Физика
Секция: Химическая физика, в том числе физика горения и взрыва
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
МОДЕЛИРОВАНИЕ ФИЛЬТРАЦИОННОГО ГОРЕНИЯ СИСТЕМЫ УГЛЕРОД – ИНЕРТНЫЙ МАТЕРИАЛ ПРИ ПОСЛОЙНОЙ ЗАГРУЗКЕ
Вагнер Сергей Александрович
инженер, ИПХФ РАН, Черноголовка
Е-mail: vagnerserge@gmail.com
Салганский Евгений Александрович
канд. физ.- мат. наук, ст. науч. сотр., ИПХФ РАН, Черноголовка
Работа выполнена при частичной финансовой поддержке ФЦП "Научные и научно-педагогические кадры инновационной России" на 2009-2013 годы ГК 14.740.11.1093
Под фильтрационным горением (ФГ) понимается распространение волн экзотермического превращения в пористой среде при фильтрации газа. Механизм распространения зоны реакции в таких системах обычно включает прогрев исходных веществ перед фронтом и локальное химическое взаимодействие реагентов с выделением большого количества тепла [1—3]. ФГ представляет собой особый вид процессов горения, активно использующийся в различных технологических процессах.

Рис.1. Принципиальная схема.
При ФГ твердых топлив может наблюдаться неустойчивость фронта горения. Для борьбы с неустойчивостью горения, например, с искривлением фронта волны горения, может применяться послойная загрузка шихты. Целью исследования являлось изучение влияния организации процесса при послойной загрузке шихты на характеристики горения.
Математическая постановка задачи. Рассматривается воздушная газификация смеси частиц углерода с инертным материалом при спутном распространении волны горения и вынужденной фильтрации воздуха в вертикальном неадиабатическом реакторе. Загрузка шихты происходит послойно: слой углерода – слой инертного материала. Принципиальная схема показана на рис. 1. Для формулировки математической модели примем допущения: рассматриваем процесс в одномерном приближении в рамках однотемпературной модели; реактор неадиабатический; перепад давления мал и давление по всему реактору принимаем равным 1 атм; химическая реакция происходит с образованием единственного продукта С+О2=СО2; скорость химической реакции записываем в аррениусовском виде с первым порядком по концентрации каждого реагента; используется уравнение состояния идеального газа. С учетом сделанных предположений процесс описывается следующими уравнениями:
Закон сохранения энергии:
 (1)
(1)
где  ,
,  ;
;
Закон сохранения массы углерода:
 (2)
(2)
Закон сохранения массы кислорода:
![]() (3)
(3)
Уравнение состояния идеального газа:
![]() (4)
(4)
Выражение для расхода газа:
![]() (5)
(5)
Выражение для скорости химической реакции:
![]() (6)
(6)
Краевые условия:
 (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
где T – температура, t – время, ![]() - пористость,
- пористость, ![]() - плотность газа,
- плотность газа, ![]() - плотность углерода,
- плотность углерода, ![]() - плотность воздуха, c - теплоемкость газа,
- плотность воздуха, c - теплоемкость газа, ![]() - коэффициент теплопроводности газа,
- коэффициент теплопроводности газа, ![]() - скорость газа,
- скорость газа, ![]() - коэффициент теплоотдачи из закона Ньютона, r- радиус реактора,
- коэффициент теплоотдачи из закона Ньютона, r- радиус реактора, ![]() - тепловой эффект химической реакции,
- тепловой эффект химической реакции, ![]() - скорость химической реакции,
- скорость химической реакции, ![]() - степень черноты,
- степень черноты, ![]() - постоянная из закона Стефана-Больцмана,
- постоянная из закона Стефана-Больцмана, ![]() - давление, R – универсальная газовая постоянная,
- давление, R – универсальная газовая постоянная, ![]() - расход газа, E – энергия активации,
- расход газа, E – энергия активации, ![]() – удельная газовая постоянная, E – энергия активации,
– удельная газовая постоянная, E – энергия активации, ![]() - предэкспонент, z – пространственная координата по реактору, L – длина реактора.
- предэкспонент, z – пространственная координата по реактору, L – длина реактора.
Индексы: s – твердая фаза; g – газ; x – кислород, с – углерод; i – инертный компонент,0 – начальное значение.
Система уравнений решалась по явной разностной схеме, где конвективные слагаемые аппроксимируются разностями против потока [4]. Шаг по времени выбирался из условий устойчивости, которые возникают в связи с явностью схемы и типа уравнений:
Выражение для скорости химической реакции:
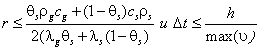 (10)
(10)
где ![]() - число Куранта.
- число Куранта.
Результаты расчета. Задача решалась в размерных переменных со следующими значениями характеристик процесса:
![]() =1000 Дж/(кг·К),
=1000 Дж/(кг·К),![]() =1300 Дж/(кг·К),
=1300 Дж/(кг·К), ![]() =1500 Дж/(кг·К),
=1500 Дж/(кг·К), ![]() =0.022 Вт/м·К,
=0.022 Вт/м·К, ![]() =1 Вт/м·К,
=1 Вт/м·К, ![]() =1 Вт/м2·К,
=1 Вт/м2·К, ![]() =0.5,
=0.5, ![]() =0.5,
=0.5, ![]() =400
=400 ![]() ,
, ![]() =900
=900 ![]() ,
,
![]() =1.19
=1.19 ![]() ,
, ![]() , E=75000.0 Дж/моль, Q=30000000 Дж/кг,
, E=75000.0 Дж/моль, Q=30000000 Дж/кг,
![]() =1500 м3/кг·с,
=1500 м3/кг·с, ![]() =10 Вт/м2·К,
=10 Вт/м2·К, ![]() =0.7,
=0.7,![]() =
=![]() , r=0.001.
, r=0.001.
Сначала проводился расчет волны ФГ в чистом углероде по модели (1)—(9) с исходными данными, описанными выше. На рис.2 представлены распределения температуры, концентрации кислорода и насыпной плотности углерода по реактору в последовательные моменты времени через 10 секунд.

Рис. 2 а – распределения температуры, б - распределения концентрации кислорода, в – распределения насыпной плотности углерода
Нагретый газ, состоящий из газообразных продуктов реакции и инертных составляющих воздуха, прогревает слои вещества перед фронтом волны горения. А твердые продукты реакции разогревают газ после фронта волны горения. Кислород расходуется полностью, для углерода в рамках данной модели имеет место не полное выгорание. Волна горения довольно растянутая, так как существенен конвективный теплообмен.
При расчете определялись время и координата по реактору при которых волна достигает стационарного состояния по всем параметрам. Дольше всего стационарного состояния достигает ширина волны. На рис. 3 представлена зависимость ширины волны (H) от времени. Под шириной волны будем понимать расстояние по реактору, где температура выше 400 K. Из графика видно, что ширина волны принимает постоянное значение равное 3.75 см приблизительно через 4 мин. На рис. 2 а красным выделен температурный профиль в момент достижения стационарного состояния.

Рис.3 – Зависимость ширины волны ФГ от времени.
Далее рассматривалась волна ФГ при послойной загрузке шихты: инертный материал -углерод. Выяснялись особенности процесса горения в зависимости от величины равной отношению ширины слоя инертного материала к ширине слоя углерода (β=hc/hi). Величина β варьировалась в диапазоне 0.4—1.0. На рис.4 представлены принципиальная схема реактора, распределения температуры, концентрации кислорода, насыпной плотности углерода и скорости фронта волны по реактору в последовательные моменты времени через 6 секунд, при β=0.5. Красными линиями выделены слои инертного материала. Из графиков хорошо виден характер горения при послойной загрузке.
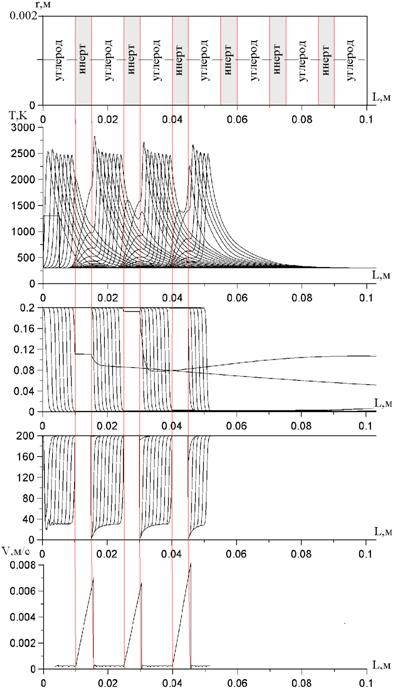
Рис. 4 а – принципиальная схема реактора, б – распределения температуры, в – распределения концентрации кислорода, г – распределения насыпной плотности углерода, д – распределения скорости фронта волны ФГ.
Когда фронт горения доходит до слоя инертного вещества, волна погасает, но за счет интенсивного теплообмена, за слоем начинает развиваться новая волна горения, т. е. воспламеняется следующий слой углерода. Причем в процессе формирования волны горения, возникает «всплеск» температуры. При расчете скорости за координату фронта горения принимали точку с максимальной температурой. Было получено следующее значение скорости в чистом углероде – 0.24 мм/с. «Всплески» температуры можно объяснить следующим образом: фронт волны горения очень быстро проскакивает инертный слой, что можно увидеть из рис. 4 д для скорости фронта, при этом инертный слой остается прогретым. Таким образом, образовавшаяся волна горения сразу за инертным слоем, некоторое время получает дополнительное тепло в зону реакции вместе с газом, разогретым от инертного слоя, что способствует образованию более высокой температуры и более полному выгоранию углерода.
В дальнейших расчетах величина β увеличивалась и при βкр=0.9 волна горения за инертным слоем не развивается, так как температура не достаточно высокая для воспламенения. Данное соотношение ширин слоев можно считать критическим в рамках данной модели. На рис. 5 представлено распределение температуры по реактору в последовательные моменты времени через 6 сек для βкр. Красными линиями выделен инертный слой.

Рис. 5 – Распределения температуры при критическом соотношении β
Из работы можно сделать вывод, что послойная организация процесса приводит к локальному подъему температуры горения, при прохождении фронта горения через инертный слой. Также существует критическое соотношение ширины слоев, больше которого распространение волны горения по шихте невозможно.
Список литературы:
1.Алдушин А.П., Мержанов А.Г. Теория фильтрационного горения: общие представления и состояния исследования / в сб. Распространение тепловых волн в гетерогенных средах, под ред. Ю.Ш. Матроса, М: Наука, Новосибирск, 1988, С. 9—49
2.Салганский Е.А., Фурсов В.П., Глазов С.В., Салганская М.В., Манелис Г.Б. Модель воздушной газификации твердого горючего в фильтрационном режиме // Физика горения и взрыва, 2003, Т. 39, № 1, С. 44—50.
3.Салганский Е.А., Кислов В.М., Глазов С.В., Жолудев А.Ф., Манелис Г.Б. Фильтрационное горение смеси углерод - инертный материал в режиме со сверхадиабатическим разогревом // Физика горения и взрыва, 2008, Т. 44, № 3, С. 30—38.
4.Самарский А.А., Николаев Е.С. Методы решений сеточных уравнений. М.: Наука. 1978. 592 с.
дипломов

Комментарии (1)
Оставить комментарий