Статья опубликована в рамках: VI Международной научно-практической конференции «Физико-математические науки и информационные технологии: проблемы и тенденции развития» (Россия, г. Новосибирск, 25 сентября 2012 г.)
Наука: Математика
Секция: Дифференциальные уравнения, динамические системы и оптимальное управление
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
СВОЙСТВА СИНГУЛЯРНОГО МАТРИЧНОГО УРАВНЕНИЯ РИККАТИ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
Копец Мирослав Михайлович
канд. физ.-мат. наук, доцент НТУУ «КПИ», г. Киев
E-mail: miroslav1941@windowslive.com
Введение
Обычно сингулярная система линейных уравнений с частными производными имеет следующий вид
![]() ,
, ![]() ,
, ![]() , (1)
, (1)
где ![]() ,
, ![]() ,
, ![]() — заданные постоянные матрицы размера
— заданные постоянные матрицы размера ![]() ,
, ![]() — искомая
— искомая ![]() вектор — функция, причем
вектор — функция, причем ![]() , то есть матрица
, то есть матрица ![]() является вырожденной; переменная
является вырожденной; переменная ![]() ассоциируется со временем,
ассоциируется со временем, ![]() — пространственная переменная,
— пространственная переменная, ![]() ,
, ![]() ,
, ![]() — заданные действительные числа,
— заданные действительные числа, ![]() —
— ![]() -мерный действительный вектор-столбец, в дальнейшем называемый состоянием системы (1). Такие системы называют по-разному: алгебро-дифференциальные системы; вырожденные системы; дифференциально-алгебраические системы; системы не типа Коши-Ковалевской; системы, не разрешенные относительно производных; дескрипторные системы; сингулярные системы; системы с вырождением. Однако независимо от названия всех их объединяет одно общее свойство: матрица
-мерный действительный вектор-столбец, в дальнейшем называемый состоянием системы (1). Такие системы называют по-разному: алгебро-дифференциальные системы; вырожденные системы; дифференциально-алгебраические системы; системы не типа Коши-Ковалевской; системы, не разрешенные относительно производных; дескрипторные системы; сингулярные системы; системы с вырождением. Однако независимо от названия всех их объединяет одно общее свойство: матрица ![]() — вырожденная (
— вырожденная (![]() ). Возможны также случаи, когда обе матрицы
). Возможны также случаи, когда обе матрицы ![]() и
и ![]() — вырожденные. Сингулярным системам со сосредоточенными параметрами посвящены, например, работы [6—8] . Там же можно найти обширную библиографию по данному вопросу. Сингулярные системы с распределенными параметрами менее исследованы. В частности, такие системы изучались в работах [1—2]. В качестве простого иллюстративного примера, который приводит к сингулярной системе (1), можно рассмотреть телеграфное уравнение [5, с. 215]:
— вырожденные. Сингулярным системам со сосредоточенными параметрами посвящены, например, работы [6—8] . Там же можно найти обширную библиографию по данному вопросу. Сингулярные системы с распределенными параметрами менее исследованы. В частности, такие системы изучались в работах [1—2]. В качестве простого иллюстративного примера, который приводит к сингулярной системе (1), можно рассмотреть телеграфное уравнение [5, с. 215]:
![]() . (2)
. (2)
С помощью введения новых переменных:

уравнение (2) можно свести к следующей системе трех уравнений:

где матрицы ![]() ,
, ![]() ,
,![]() соответственно равны:
соответственно равны:
 ,
,  ,
,  .
.
К сингулярным системам относят также и такие системы вида (1), когда все три матрицы ![]() ,
, ![]() ,
,![]() — прямоугольные матрицы одинакового размера.
— прямоугольные матрицы одинакового размера.
Вспомогательные сведения
Пусть объект управления описывается следующей системой линейных уравнений с частными производными
![]() , (3)
, (3)
где ![]() ,
, ![]() ,
, ![]() — заданные матрицы размера
— заданные матрицы размера ![]() ,
, ![]() — заданная матрица размера
— заданная матрица размера ![]() , причем все эти четыре матрицы — постоянные (их элементами являются действительные числа) и
, причем все эти четыре матрицы — постоянные (их элементами являются действительные числа) и ![]() . Переменная
. Переменная ![]() ,
, ![]() ассоциируется со временем, переменная
ассоциируется со временем, переменная ![]() ,
, ![]() , является пространственной переменной,
, является пространственной переменной, ![]() ,
, ![]() и
и ![]() — заданные действительные числа,
— заданные действительные числа, ![]() — действительный
— действительный ![]() -мерный вектор-столбец, в дальнейшем называемый состоянием системы (3), действительный
-мерный вектор-столбец, в дальнейшем называемый состоянием системы (3), действительный ![]() -мерный вектор-столбец
-мерный вектор-столбец ![]() называется управлением. Предполагается, что управления принадлежат классу кусочно-непрерывных вектор-функций. Для системы (3) задано начальное условие
называется управлением. Предполагается, что управления принадлежат классу кусочно-непрерывных вектор-функций. Для системы (3) задано начальное условие
![]() (4)
(4)
и граничное условие
![]() . (5)
. (5)
Действительные ![]() -мерные вектор-столбцы
-мерные вектор-столбцы ![]() и
и ![]() известны. Считаем, что для каждого заданного управления
известны. Считаем, что для каждого заданного управления ![]() система уравнений (3) имеет единственное решение, которое удовлетворяет условиям (4) и (5).
система уравнений (3) имеет единственное решение, которое удовлетворяет условиям (4) и (5).
Рассмотрим следующий критерий оптимальности
![]()
 , 6)
, 6)
где выражение ![]() означает скалярное произведение векторов
означает скалярное произведение векторов ![]() и
и ![]() , то есть
, то есть ![]() ,
, ![]() —
—
заданная симметричная положительно определенная матрица размера ![]() (следовательно, существует матрица
(следовательно, существует матрица![]() ),
), ![]() и
и ![]() также известные симметричные неотрицательно определенная матрицы размера
также известные симметричные неотрицательно определенная матрицы размера ![]() . Задача оптимального управления объектом, описываемым системой соотношений (3) — (5), состоит в определении такого управления
. Задача оптимального управления объектом, описываемым системой соотношений (3) — (5), состоит в определении такого управления ![]() , при котором функционал (6) принимает наименьшее значение. Если такое управление
, при котором функционал (6) принимает наименьшее значение. Если такое управление ![]() существует, то оно называется оптимальным управлением.
существует, то оно называется оптимальным управлением.
Как правило, для нахождения решения задач оптимального управления системами как и со сосредоточенными параметрами, так и с распределенными параметрами, используется принцип максимума Л.С. Понтрягина [4, с. 183] или метод динамического программирования Беллмана [4, с. 291]. Оба этих метода предполагают, что система дифференциальных уравнений, которая описывает поведение объекта управления, разрешена относительно производных по времени. В случае сингулярных систем такой возможности нет. Однако можно воспользоваться методом множителей Лагранжа [4, с. 31]. Сущность метода состоит в том, что вместо функционала (6) рассматривается следующий функционал
![]()
![]()
![]() , (7)
, (7)
где ![]() — неизвестная
— неизвестная ![]() вектор-функция. Очевидно, что при выполнении соотношения (3) значения функционалов (6) и (7) совпадают. Поэтому задача на условный экстремум для функционала (6) сводится к задаче на безусловный экстремум для функционала (7). Дальше находим выражение для приращения
вектор-функция. Очевидно, что при выполнении соотношения (3) значения функционалов (6) и (7) совпадают. Поэтому задача на условный экстремум для функционала (6) сводится к задаче на безусловный экстремум для функционала (7). Дальше находим выражение для приращения ![]() функционала (7).
функционала (7).
![]()
После несложных преобразований находим для ![]() следующую формулу (см. [3])
следующую формулу (см. [3])
![]()
![]()
![]()

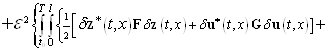
![]()
![]() . (8)
. (8)
Полученное выражение для ![]() дает возможность сформулировать следующее утверждение.
дает возможность сформулировать следующее утверждение.
Теорема 1. Единственное оптимальное управление ![]() , которое реализует минимум функционала (6), определяется из таких соотношений:
, которое реализует минимум функционала (6), определяется из таких соотношений:
 (9)
(9)
Доказательство этого утверждения приведено в работе [3]. Исходя из системы уравнений (9) и соотношения ![]() можно получить следующие уравнения:
можно получить следующие уравнения:
![]()
![]() , (10)
, (10)
![]() , (11)
, (11)
![]() ,
,![]() ,
,![]() , (12)
, (12)
где ![]() — неизвестная матричнозначная функция. Уравнение типа (10) будем называть сингулярным матричным дифференциальным уравнение Риккати с частными производными.
— неизвестная матричнозначная функция. Уравнение типа (10) будем называть сингулярным матричным дифференциальным уравнение Риккати с частными производными.
Свойства сингулярного матричного уравнения Риккати с частными производными
Применяя к равенству (10) операцию транспонирования, приходим к такому соотношению
![]()
![]() . (13)
. (13)
Условия (11) и (12) после транспонирования соответственно примут вид
![]() , (14)
, (14)
![]() ,
, ![]() ,
,![]() . (15)
. (15)
Кроме того, из равенства (14) имеем
![]() . (16)
. (16)
Таким образом, обе функции ![]() и
и ![]() являются решениями одного и того же уравнения (10) и удовлетворяют одним тем же условиям (11) и (12). Поэтому справедливо следующее утверждение.
являются решениями одного и того же уравнения (10) и удовлетворяют одним тем же условиям (11) и (12). Поэтому справедливо следующее утверждение.
Теорема 2. Если задача (10) — (12) имеет единственное решение, то справедливо равенство ![]() , то есть для каждой упорядоченной пары
, то есть для каждой упорядоченной пары ![]() где
где![]() решение
решение ![]() есть симметрической матрицей порядка
есть симметрической матрицей порядка ![]() .
.
Теорема 3. Если ![]() — решение задачи (10) — (12), то имеет место соотношение
— решение задачи (10) — (12), то имеет место соотношение
![]() , (17)
, (17)
где функции ![]() и
и ![]() удовлетворяют системе уравнений
удовлетворяют системе уравнений
 (18)
(18)
и дополнительным условиям
![]() ,
,![]() , (19)
, (19)
при условии, что матричнозначная функция ![]() существует. Также выполняются равенства
существует. Также выполняются равенства ![]() ,
, ![]() .
.
Доказательство. Предположим, что существует матрица ![]() и имеет место следующая зависимость
и имеет место следующая зависимость
![]() , (20)
, (20)
где ![]() и
и ![]() — неизвестные пока функции. Выполнив в равенстве (20) операцию транспонирования, получим
— неизвестные пока функции. Выполнив в равенстве (20) операцию транспонирования, получим
![]() . (21)
. (21)
Дальше рассмотрим очевидное тождество
![]() . (22)
. (22)
Подставляя в левую часть (22) значение ![]() из (20), а в правую часть
из (20), а в правую часть ![]() из (22), получаем следующее соотношение
из (22), получаем следующее соотношение
![]() , (23)
, (23)
которое в дальнейшем будет использовано.
Из соотношения (20) имеем
![]() (24)
(24)
и
![]() . (25)
. (25)
Подставляя (20), (21), (24) и (25) в уравнение (10), получим
![]()
![]()
![]() . (26)
. (26)
После умножения равенства (26) справа на матрицу ![]() , имеем
, имеем
![]()
![]() . (27)
. (27)
Если теперь предположить, что выполняется соотношение
![]() , (28)
, (28)
то равенство (27) примет вид
![]()
![]() . (29)
. (29)
Теперь, принимая во внимание соотношения (11), (20) и (21), получим
![]() .
.
С учетом этого равенства и соотношения (23) уравнение (29) можно переписать следующим образом
![]()
![]()
или
![]() .
.
Последнее соотношение будет выполнено, если имеет место равенство
![]() . (30)
. (30)
Таким образом, объединяя соотношения (28) и (30), в результате получаем следующую систему матричных уравнений с частными производными
 . (31)
. (31)
Условие (11) приводит к такому равенству
![]() .
.
Если это равенство умножить слева на матрицу![]() и справа на матрицу
и справа на матрицу ![]() , то в результате получим
, то в результате получим
![]() .
.
Из равенства ![]() имеем
имеем ![]() или
или ![]() . Из условий
. Из условий ![]() и равенства
и равенства ![]() получаем
получаем ![]() .
.
Теорема 4. Если рассмотреть блочную матрицу ![]() размера
размера ![]()
![]() , (32)
, (32)
то систему уравнений (31) можно записать в таком виде
 , (33)
, (33)
где ![]() — квадратная матрица размера
— квадратная матрица размера ![]() , все элементы которой равны нулю.
, все элементы которой равны нулю.
Доказательство. Действительно, путем непосредственного вычисления находим
 .
.
Подобным образом устанавливается и следующее утверждение.
Теорема 5. С помощью матрицы (32) систему уравнений (10) — (11) можно записать в блочной форме
 , (34)
, (34)
где ![]() — единичная матрица размера
— единичная матрица размера ![]() ,
, ![]() — квадратная матрица размера
— квадратная матрица размера ![]() , все элементы которой равны нулю.
, все элементы которой равны нулю.
Доказательство. В самом деле, имеем

 .
.
Дальше находим

 .
.
Таким образом, окончательно получим
![]()
![]() ,
,
поскольку ![]() . Это означает, что равенство (34) доказано.
. Это означает, что равенство (34) доказано.
Теорема 6. Пусть функция ![]() — частное решение уравнений (10) — (12). Если
— частное решение уравнений (10) — (12). Если ![]() — некоторое другое решение задачи (10) — (12), отличное от
— некоторое другое решение задачи (10) — (12), отличное от ![]() , то функция
, то функция ![]() является решением матричного уравнения Бернулли с частными производными
является решением матричного уравнения Бернулли с частными производными
![]() , (35)
, (35)
где ![]() ,
, ![]() . При этом выполняются равенства
. При этом выполняются равенства ![]() ,
,![]() ,
, ![]() и
и ![]() .
.
Доказательство. Из равенства ![]() непосредственно имеем
непосредственно имеем ![]() и
и ![]() . Подставляя эти выражения в уравнение (10), получим:
. Подставляя эти выражения в уравнение (10), получим:
![]()
![]()
![]()
![]() . (36)
. (36)
Согласно условию теоремы 6 имеет место равенство
![]()
![]() .
.
С учетом этого соотношения из (36) находим
![]()
![]() .
.
Если ввести обозначение ![]() , то тогда
, то тогда ![]() , и последнее соотношение примет вид
, и последнее соотношение примет вид
![]()
Дальше из равенства ![]() имеем
имеем ![]() . Из соотношений
. Из соотношений ![]() ,
,![]() и
и ![]() получаем
получаем![]() ,
,![]() . Также из равенств
. Также из равенств ![]() ,
, ![]() ,
,![]() соответственно находим
соответственно находим ![]() ,
,![]() . Это означает, что теорема 6 полностью доказана.
. Это означает, что теорема 6 полностью доказана.
Теорема 7. С помощью замены ![]() уравнение (35) сводится к линейному уравнению
уравнение (35) сводится к линейному уравнению ![]() . При этом должно выполняться условие
. При этом должно выполняться условие ![]() .
.
Доказательство. Поскольку верно равенство ![]() , то используя формулы
, то используя формулы ![]() и
и ![]() , имеем
, имеем ![]() . Кроме того, из тождества
. Кроме того, из тождества ![]() очевидным способом получаем
очевидным способом получаем ![]() . С помощью формулы для производной обратной матрицы имеем
. С помощью формулы для производной обратной матрицы имеем ![]() и
и ![]() . Подставляя эти выражения в уравнение (35), получим
. Подставляя эти выражения в уравнение (35), получим
![]() .
.
Используя теперь соотношения ![]() и
и ![]() , последнее равенство перепишем так
, последнее равенство перепишем так
![]() .
.
Если теперь это равенство умножить слева на матрицу![]() , то окончательно находим
, то окончательно находим
![]() . (37)
. (37)
Учитывая равенство ![]() , получим
, получим ![]() . Таким образом, теорема 7 полностью доказана.
. Таким образом, теорема 7 полностью доказана.
Пусть известно частное решение ![]() уравнения (37). Тогда это уравнение можно свести к однородному уравнению, если выполнить замену.
уравнения (37). Тогда это уравнение можно свести к однородному уравнению, если выполнить замену.
![]() . (38)
. (38)
На основании (38) имеем
![]() (39)
(39)
и
![]() ,
, ![]() . (40)
. (40)
Подставляя (38) — (40) в уравнение (37), находим
![]()
![]() . (41)
. (41)
Согласно предположению справедливо равенство
![]() .
.
Поэтому из (41) имеем
![]() . (42)
. (42)
Таким образом, доказано следующее утверждение.
Теорема 8. Если матричнозначная функция ![]() является решением уравнения (37), то с помощью замены (38) уравнение (37) сводится к однородному линейному уравнению (42).
является решением уравнения (37), то с помощью замены (38) уравнение (37) сводится к однородному линейному уравнению (42).
Решение уравнения (42) можно искать в виде следующего произведения ![]() , где
, где ![]() — произвольная постоянная матрицы размера
— произвольная постоянная матрицы размера ![]() ,
, ![]() и
и ![]() — неизвестные матрицы такого же размера. Отсюда следует, что
— неизвестные матрицы такого же размера. Отсюда следует, что
![]() ,
,
![]()
и ![]() . Подставляя эти выражения в уравнение (42), имеем
. Подставляя эти выражения в уравнение (42), имеем
![]()
![]() .
.
Это равенство запишем в следующей эквивалентной форме
![]()
![]() . 43)
. 43)
Если теперь функцию ![]() выбрать так, чтобы выполнялось равенство
выбрать так, чтобы выполнялось равенство
![]() , (44)
, (44)
то соотношение (43) будет выглядеть так
![]() . 45)
. 45)
Поскольку имеет место соотношение ![]() , то отсюда находим
, то отсюда находим ![]() . Из равенств
. Из равенств ![]() ,
, ![]() имеем
имеем ![]() . Так как
. Так как ![]() и
и ![]() , то можно написать равенство
, то можно написать равенство ![]() или
или ![]() , если матрица
, если матрица ![]() существует. Также из равенства
существует. Также из равенства ![]() получаем
получаем ![]() . С учетом этих замечаний вместо уравнения (45) получим следующее уравнение
. С учетом этих замечаний вместо уравнения (45) получим следующее уравнение
![]()
или
![]() .
.
Умножая справа последнее равенство на матрицу ![]() , находим
, находим
![]() .
.
Если теперь в этом уравнении сделать замену ![]() и учесть, что
и учесть, что ![]() и
и ![]() , то окончательно находим
, то окончательно находим
![]() . (46)
. (46)
В результате приходим к следующему утверждению.
Теорема 9. Решение уравнения (42) имеет вид ![]() , где
, где ![]() — произвольная постоянная матрицы размера
— произвольная постоянная матрицы размера ![]() ,
, ![]() и
и ![]() — матричнозначные функции такого же размера, удовлетворяющие уравнениям (44) и (46) соответственно при условии, что матрица
— матричнозначные функции такого же размера, удовлетворяющие уравнениям (44) и (46) соответственно при условии, что матрица ![]() существует.
существует.
Уравнение (10) можно представить в симметрической форме. В самом деле, из условия ![]() следует, что
следует, что ![]() . Поэтому
. Поэтому ![]() и
и ![]() . Отсюда следует, что уравнение (10) можно переписать так
. Отсюда следует, что уравнение (10) можно переписать так
![]()
![]() . (47)
. (47)
Уравнение (47) естественным образом порождает следующую блочную матрицу
 (48)
(48)
размера ![]() .
.
Теорема 10. С помощью матрицы (48) уравнение (47) можно представить таким образом
 .
.
Доказательство. С помощью непосредственного вычисления находим
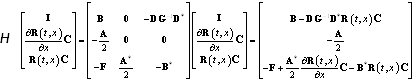
 \
\

![]() ,
,
что и требовалось доказать.
Вычисление минимального значения критерия оптимальности
На основании формулы Ньютона-Лейбница имеем
![]()
![]() .
.
Так как имеет место равенство ![]() , то отсюда непосредственно находим
, то отсюда непосредственно находим
![]()
![]() . (49)
. (49)
С учетом этого замечания функционал (6) можно представить таким образом
![]()
![]() . (50)
. (50)
Согласно формуле дифференцирования произведения трех сомножителей получим
![]()
![]() . (51)
. (51)
С учетом соотношения (51) функционал (50) примет вид
![]()
![]()
![]() . (52)
. (52)
Подставляя выражение ![]() в уравнение (3), имеем
в уравнение (3), имеем
![]() . (53)
. (53)
Выполняя операцию транспонирования в соотношении (53) . получим
![]() . (54)
. (54)
Поскольку ![]() , то
, то ![]() и
и
![]() . (55)
. (55)
Дальше на основании соотношений (53) и (54) находим
![]()
![]() , (56)
, (56)
![]()
![]() , (57)
, (57)
С учетом соотношений (55) — (57) функционал (52) примет вид
![]()
![]()
![]()
![]()
![]()
![]()
![]() . (58)
. (58)
Поскольку справедливы равенства ![]() , то на основании формулы Ньютона-Лейбница получим
, то на основании формулы Ньютона-Лейбница получим
. (59)
Из очевидного соотношения
![]()
![]() ,
,
с учетом равенства (59) находим
![]()
![]() .(60)
.(60)
Теперь принимая во внимание соотношение (60) и приводя подобные члены в (58), имеем
![]()
![]()
![]()
![]() .
.
Поскольку справедливы соотношения (10) и (11), то окончательно получим
![]() . (61)
. (61)
Теорема 11. Минимальное значение функционала (4)
вычисляется по формуле (61), где функция ![]() — решение матричного уравнения с частными производными (10) и удовлетворяет дополнительными условиям (11) — (12).
— решение матричного уравнения с частными производными (10) и удовлетворяет дополнительными условиям (11) — (12).
Список литературы:
1.Бормотова О.В., Гайдомак С.В., Чистяков В.Ф.В. О разрешимости вырожденных систем дифференциальных уравнений в частных производных. // Изв. вузов. Математика. — 2005. — № 4 (515). — С. 18—29.
2.Бормотова О.В., Чистяков В.Ф. В. О методах численного решения и исследования систем не типа Коши-Ковалевской. // Журн. вычисл. матем. и мат. физики. — 2004. — Т. 44, № 8. — С. 1380—1387.
3.Копец М.М. Оптимальное управление объектом, описываемым сингулярной системой линейных уравнений с частными производными. // «Математика и информационные технологии в современном мире», материалы международной заочной научно-практической конференции. — Новосибирск, 2011. — с. 5—17.
4.Сиразетдинов Т.К. Оптимизация систем с распределенными параметрами. М.: Наука, 1977. — 480 с.
5.Фарлоу С. Уравнения с частными производными для научных работников и инженеров: Пер. с англ. М.: Мир, 1985. — 384 с.
6.Campbell S.L. Singular system of differential equations. Research Notes in Math., No 40. San Francisco: Pitman, 1980. — 176 p.
7.Campbell S.L. Singular system of differential equations. II. Research Notes in Math., No 61. San Francisco: Pitman, 1982. — 234 p.
8.Kunkel P., Mehrmann V. Differential-Algebraic Equations. Analysis and Numerical Solution. Printed in Germany, 2006. — 377 p.
дипломов

Оставить комментарий