Статья опубликована в рамках: IV Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 01 апреля 2013 г.)
Наука: Математика
Секция: Вещественный, комплексный и функциональный анализ
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ОБОБЩЕННАЯ КОМПЛЕКСНАЯ ЭКСПОНЕНТА И ЕЁ ПРИМЕНЕНИЯ ДЛЯ ОТЫСКАНИЯ СУММЫ
Сагиндыков Бимурат Жумабекович
канд. физ.-мат. наук, доцент КазНТУ, г. Алматы
Бимурат Жанар
Магистрант ENSG, г. Nancy
E-mail: bimurat55@gmail.com
В данной статье рассматривается обобщенная комплексная экспонента. Описанная в статье методика позволяет найти некоторые конечные суммы показательно — тригонометрических рядов.
Ключевые слова: обобщенное комплексное число, комплексная экспонента, формула Эйлера, ряды, конечные суммы.
Введение
Обобщенная комплексная экспонента — математическая функция, задаваемая соотношением ![]() , где
, где ![]() ,
, ![]() есть обобщенное комплексное число. Обобщенная комплексная экспонента определяется как аналитическое продолжение экспоненты
есть обобщенное комплексное число. Обобщенная комплексная экспонента определяется как аналитическое продолжение экспоненты ![]() вещественного переменного х. Определим формальное выражение
вещественного переменного х. Определим формальное выражение ![]() . Определенное таким образом выражение на вещественной оси будет совпадать с классической вещественной экспонентой. Для полной корректности построения необходимо доказать аналитичность функции
. Определенное таким образом выражение на вещественной оси будет совпадать с классической вещественной экспонентой. Для полной корректности построения необходимо доказать аналитичность функции ![]() , то есть показать, что
, то есть показать, что ![]() разлагается в некоторый сходящийся к данной функции ряд. Покажем это:
разлагается в некоторый сходящийся к данной функции ряд. Покажем это:
![]() ,
,
где: ![]() , а
, а ![]() ,
, ![]() — вещественные числа. Сходимость данного ряда легко доказывается:
— вещественные числа. Сходимость данного ряда легко доказывается:

Ряд всюду сходится абсолютно, то есть вообще всюду сходится, таким образом, сумма этого ряда в каждой конкретной точке будет определять значение аналитической функции ![]() .
.
Единственным обобщением вещественных чисел с сохранением известных законов арифметики являются комплексные числа. Поэтому мы здесь займемся обобщением только внутреннего строения комплексных чисел. Обобщенное комплексное число ![]() можно представить в виде
можно представить в виде ![]() , где
, где ![]() . Чтобы термин соответствовал названию, рассмотрим частные случаи.
. Чтобы термин соответствовал названию, рассмотрим частные случаи.
Если ![]() ,
, ![]() ,
, ![]() , то обобщенному комплексному числу соответствует обычное комплексное число
, то обобщенному комплексному числу соответствует обычное комплексное число ![]() .
.
Если ![]() ,
, ![]() ,
, ![]() , то обобщенному комплексному числу соответствует двойное число.
, то обобщенному комплексному числу соответствует двойное число.
Если ![]() ,
, ![]() , то обобщенному комплексному числу соответствует дуальное число.
, то обобщенному комплексному числу соответствует дуальное число.
Меняя управляющие параметры ![]() ,
, ![]() , получаем разные теории.
, получаем разные теории.
Приступая к изложению обобщенных комплексных вида ![]() , определим сложение, умножение и сопряжение таких выражений по формулам:
, определим сложение, умножение и сопряжение таких выражений по формулам:
сложение ![]()
произведение ![]()
сопряжение ![]()
Умножение ![]() дает неотрицательное вещественное число, поэтому определяет норму обобщенного комплексного числа
дает неотрицательное вещественное число, поэтому определяет норму обобщенного комплексного числа ![]() . Таким образом
. Таким образом
![]() (1)
(1)
Правая часть (1) является квадратичной формой от двух переменных х, у.
Относительно инварианта квадратичной формы обобщенные комплексные числа делятся на типы. А именно, различают эллиптические, гиперболические и параболические комплексные числа. Это означает следующее. Пусть ![]() . Тогда числа делятся на указанные типы в зависимости от того, какими являются
. Тогда числа делятся на указанные типы в зависимости от того, какими являются ![]() и
и ![]() . Если
. Если ![]() то такие обобщенные комплексные числа относятся к эллиптическому типу, если же
то такие обобщенные комплексные числа относятся к эллиптическому типу, если же ![]() то — к гиперболическому типу, если
то — к гиперболическому типу, если ![]() то — к параболическому типу.
то — к параболическому типу.
Для обобщенных комплексных чисел отметим также формулу Эйлера
![]()
 (2)
(2)
истинная природа, которой будет выявлена в дальнейшем. Наиболее простое доказательство этой формулы получается с использованием теории дифференциальных уравнений.
В тождестве (2) его комплексное сопряжение дает
![]() ,
,
или
![]() . (3)
. (3)
Умножая (2) и (3) можно легко получить основное показательно — тригонометрическое тождество для обобщенно — комплексных чисел
![]() . (4)
. (4)
1. Формулы сложения
По принятому соглашению ![]() С другой стороны
С другой стороны ![]() Отсюда отделяя вещественные и мнимые части относительно параметра р имеем:
Отсюда отделяя вещественные и мнимые части относительно параметра р имеем:
![]() (5)
(5)
где: ![]() .
.
Пример 1. Пусть ![]() ,
, ![]() ,
, ![]()
![]()
Тогда из (2), (5) следуют следующие формулы сложения
![]()
![]()
Если в формулах (5) принять ![]() мы получим формулы двойного аргумента
мы получим формулы двойного аргумента
 (6)
(6)
Пример 2. Пусть ![]() ,
, ![]() ,
, ![]() Тогда
Тогда ![]()
2. Отыскание сумм некоторых показательно-тригонометрических рядов
Пусть ![]() — функция обобщенного комплексного переменного
— функция обобщенного комплексного переменного ![]() , аналитическая для
, аналитическая для ![]() , где
, где ![]() . В этих условиях известно, что для
. В этих условиях известно, что для ![]() функция
функция ![]() может быть разложена в степенной ряд
может быть разложена в степенной ряд
![]() (7)
(7)
Допустим, что коэффициенты этого ряда оказались вещественными числами. Положим ![]() . Таким образом, для любого х:
. Таким образом, для любого х:
![]()
![]() (8)
(8)
![]()
Отделим в выражении ![]() действительную и мнимую части, т.е. представим
действительную и мнимую части, т.е. представим ![]() в виде
в виде
![]() ,
,
где: ![]() и
и ![]() — вещественные функции. Из (8) тогда очевидно следует, что
— вещественные функции. Из (8) тогда очевидно следует, что
![]()
![]()
Этим обстоятельством можно воспользоваться, чтобы получить суммы некоторых показательно – тригонометрических рядов.
Пример 3. Известно, что для всех ![]()

Тогда в силу (8)

С другой стороны
![]()
и поэтому
 (9)
(9)
Пример 4. Пусть ![]() ,
, ![]() ,
, ![]() Тогда в силу (9)
Тогда в силу (9)
![]()
![]()
Пример 5. Найти сумму ряда ![]() . Данный ряд является геометрической прогрессией (сходящуюся для
. Данный ряд является геометрической прогрессией (сходящуюся для ![]() ) со знаменателем
) со знаменателем ![]() . Следовательно,
. Следовательно, ![]() . По принятому соглашению
. По принятому соглашению ![]() и
и ![]() . Тогда
. Тогда

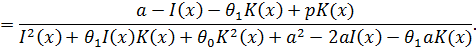
Отсюда
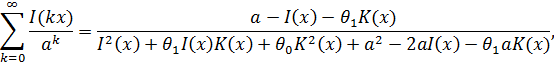

Пример 6. Пусть ![]() ,
, ![]() ,
,
 ,
, ![]() .
.
Тогда


Эти разложения справедливы для всех х, когда ![]() или
или ![]() , или
, или ![]() , т. е. когда
, т. е. когда ![]() .
.
3. Нахождение конечных сумм и рядов
Найти сумму ряда



Отсюда ![]()
![]()
где ![]()
Пример 7. Пусть ![]() ,
, ![]() ,
, ![]() . Тогда
. Тогда

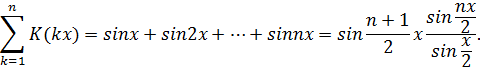
Пример 8. Пусть ![]() ,
,
 .
.
Тогда
![]()

![]()

Зная формулы понижения степени, мы можем найти конечные суммы следующих рядов: ![]() и
и ![]() , где
, где
![]()
![]()
![]()




Пример 9. Пусть ![]() ,
, ![]() . Тогда
. Тогда

Совершенно аналогично находится сумма для косинусов:

Список литературы:
1.Сагиндыков Б.Ж. Эллиптическая система чисел и ее применение // Вестник КазНТУ. — 2007. — № 4. [Электронный ресурс] — Режим доступа. — URL: http://www.e-lib.kazntu.kz/sites/default/files/articles/sagindykov_2007_4.pdf
дипломов


Оставить комментарий