ЗАДАЧА  ОПТИМАЛЬНОГО  УПРАВЛЕНИЯ  ДВУМЕРНОЙ  СИСТЕМОЙ  С  РАСПРЕДЕЛЕННЫМИ  ПАРАМЕТРАМИ

Копец  Мирослав  Михайлович

канд.  физ.-мат.  наук,  доцент  НТУУ  «Киевский  политехнический  институт»,  г.  Киев

E-mail:  optimal201214@yandex.ua

В  настоящее  время  существует  много  серьезных  монографий  и  журнальных  статей,  посвященных  проблемам  оптимального  управления  объектами  с  распределенными  параметрами.  Чтобы  убедиться  в  этом,  достаточно  упомянуть,  например,  монографии  [1]—[5].  В  каждой  из  них  также  содержится  достаточно  обширная  библиография  по  упомянутой  выше  проблеме.  Традиционно  в  большинстве  этих  работ  рассматривается  объект,  поведение  которого  описывается  одним  дифференциальным  уравнением  с  частными  производными.  Однако  не  подлежит  сомнению  тот  факт,  что  во  многих  случаях  для  составления  математической  модели  физических  процессов  возникает  необходимость  рассмотрения  системы  дифференциальных  уравнений  с  частными  производными.  Во-первых,  такая  модель  может  казаться  более  адекватной  исследуемому  процессу.  Во-вторых,  изучение  такой  модели  позволяет  получать  новые  математические  объекты,  и  существенно  продвинуться  в  исследовании  свойств  этих  объектов. 

Данная  работа  посвящена  задаче  минимизации  квадратического  функционала  на  решениях  системы  линейных  дифференциальных  уравнений  с  частными  производными  при  условии,  что  правые  части  этих  уравнений  включают  в  себя  параметры,  именуемые  управлениями.  Для  решения  упомянутой  задачи  используется  метод  множителей  Лагранжа.  Привлечение  этого  метода  дало  возможность  получить  для  данной  задачи  необходимые  условия  оптимальности.  На  основе  полученных  условий  оптимальности  предложен  вывод  матричного  интегро-дифференциального  уравнения  Риккати.

Пусть  объект  управления  описывается  следующей  системой  линейных  уравнений  с  частными  производными

,  (1)

где:  ,    и    —  заданные  матрицы  размера  , 

  —  заданная  матрица  размера  ,  причем  все  эти  три  матрицы  —  постоянные  (их  элементами  являются  действительные  числа).  Переменная    означает  время, 

  и    —  пространственные  переменные, 

  —  действительный  -мерный  вектор-столбец,  в  дальнейшем  именуемый  состоянием  системы  (1),  действительный  -мерный  вектор-столбец    называется  управлением.  Предполагается,  что  управления  принадлежат  классу  кусочно-непрерывных  вектор-функций.  Для  системы  (1)  заданы  начальное  условие 

  (2)

и  граничные  условия

,  .  (3)

Действительные  числа  ,  ,  ,  ,  -мерные  вектор-столбцы  ,    и    заданы.  В  дальнейшем  предполагаем,  что  для  каждого  заданного  управления    система  уравнений  (1)  имеет  единственное  решение,  которое  удовлетворяет  условиям  (2)  и  (3). 

Рассмотрим  следующий  критерий  оптимальности 

,  (4)

где:    и    —  заданные  неотрицательно  определенные  симметрические  матрицы  размера  , 

  —  заданная  положительно  определенная  симметрическая  матрица  размера  (следовательно,  существует  обратная  матрица  )  причем  элементами  этих  матриц  являются  действительные  числа.  Выражение    означает  скалярное  произведение  векторов    и  , 

т.  е.  .  Задача  оптимального  управления  объектом,  описываемым  системой  соотношений  (1)—(3)  при  наличии  функционала  (4),  состоит  в  определении  управления  ,  при  котором  на  решениях  краевой  задачи  (1)—(3)  функционал  (4)  принимает  наименьшее  значение.  Если  такое  управление  существует,  то  оно  называется  оптимальным  управлением.

Решение  сформулированной  выше  задачи  оптимального  управления  будем  искать  с  помощью  метода  множителей  Лагранжа  [6,  с.  31].  Сущность  метода  состоит  в  том,  что  функционал  (4)  следует  заменить  следующим  функционалом

,  (5)

Где:  —  неизвестная  мерная  вектор-функция  (множитель  Лагранжа).  Если  выполняются  равенства  (1)—(3),  то  значения  функционалов  (4)  и  (5)  совпадают.  В  результате  задача  на  условный  экстремум  для  функционала  (4)  сводится  к  задаче  на  безусловный  экстремум  для  функционала  (5).  Дальше  находим  выражение  для  приращения    функционала  (5): 

.

Легко  видеть,  что  ,  ,  ,  ,  ,  .  Дальше  имеем 

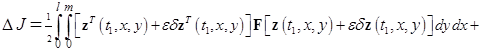
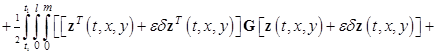
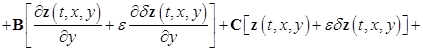
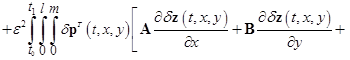
.  (6)

Очевидны  следующие  соотношения

,  (7)

,  (8)

,  (9)

,  (10)

.  (11)

Если    и  ,  то  имеют  место  равенства

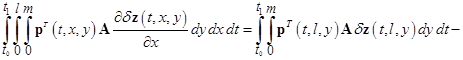
,  (12)

.  (13)

С  учетом  соотношений  (7)—(13)  выражение  (6)  будет  иметь  следующий  вид

.  (14)

Необходимое  условие  экстремума  функционала  (5)  —  равенство  нулю  его  первой  вариации.  Это  условие  будет  выполнено,  если  имеют  место  такие  равенства

,  (15)

,  (16)

,  (17)

.  (18)

Соотношения  (15)—(18)  дают  основание  для  следующего  утверждения. 

Теорема  1.  Если  задача  оптимизации  (1)—(4)  имеет  решение  ,  то  это  решение  единственно  и  определяется  из  следующих  соотношений:

   (19)

где:  символ    обозначает  транспонированную  матрицу  .  Аналогично  обозначаются  транспонированые  матрицы  ,    и  .

Доказательство.  Система  уравнений  (19)  составлена  на  основании  равенств  (15)—(18)  путем  присоединения  к  ним  начального  условия  (2),  граничных  условий  (3)  и  условий  ,.  Коэффициент  при    в  соотношении  (14)  равен

.

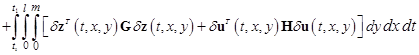В  силу  положительной  определенности  матрицы    и  неотрицательной  определенности  матриц    и  имеем  .  Это  означает,  что  управление  реализует  минимум  функционала  (5),  следовательно,  и  функционала  (4).  Доказательство  единственности  оптимального  управления  следует  из  таких  соображений.  Пусть  существует  управление  ,  на  котором  также  реализуется  минимум  функционала  (5).  Тогда  приращение  равно  нулю.  Поскольку  в  этом  случае  выполняются  равенства  (19),  то  тогда  также  и      Последнее  равенство  возможно  в  том  случае,  когда    и  .  Отсюда  следует,  что  .

Из  последнего  соотношения  системы  (19)  имеем  .  После  подстановки  этого  выражение  в  первое  из  уравнений  системы  (19)  для  нахождения    и  получим  следующую  систему  уравнений

   (20)

Дальше  ищем  матричнозначную  функцию  ,  которая  удовлетворяет  соотношению 

,  (21)

где:  и  являются  решением  системы  уравнений  (20).  Очевидно,  имеем 

,  (22)

  ,  (23)

.  (24)

Подставляя  выражение  (21)  для  в  первое  уравнение  системы  (20),  находим

.

С  учетом  этого  равенства  первое  соотношение  (22)  будет  иметь  вид

.  (25)

Дальше  в  кратном  интеграле 

сначала  меняем  порядок  интегрирования  по  переменным    и  ,  после  этого  переобозначаем    на    и,  наоборот,    на  .  В  результате  получим 

.  (26)

Дальше  в  последнем  интеграле  аналогично  поступаем  с  переменными    и  .  Это  приводит  к  следующему  соотношению

.  (27)

Полагая    и  ,  после  интегрирования  по  частям  находим

.  (28)

Подобным  образом  получим

.  (29)

С  учетом  равенств  (21)  и  (22)  соотношение  (21)  перепишется  так

.  (30)

Аналогично,  на  основании  второго  уравнения  системы  (20),  равенств  (21),  (23)  и  (24)  находим 

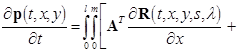
,  (31)

где:    —  двумерная  дельта-функция  Дирака.  Сопоставляя  соотношения  (30)  и  (31),  в  результате  получим

или 

.  (32)

Дальше  из  условия    и  соотношения  (21)  находим

.  (33)

Подводя  итоги,  приходим  к  следующему  заключению.

Теорема  2.  Если  задача  оптимизации  (1)—(4)  имеет  решение,  то  его  можно  найти  по  формуле 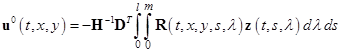 ,  где  матричнозначная  функция    есть  решением  матричного  интегро-дифференциального  уравнения  (32)  с  дополнительным  условием  (33)  и  граничными  условиями    и  ,  а  оптимальное  состояние    является  решением  матричного  интегро-дифференциального  уравнения 

,

удовлетворяет  начальному  условию  (2)  и  граничным  условиям  (3).

Список  литературы:

1.Бутковский  А.Г.  Теория  оптимального  управления  системами  с  распределенными  параметрами.  —  М.:  Наука,  1965  —  476  с.

2.Бутковский  А.Г.  Методы  управления  системами  с  распределенными  параметрами.  —  М.:  Наука,  1975  —  568  с.

3.Лионс  Ж.-Л.  Оптимальное  управление  системами,  описываемыми  уравнениями  с  частными  производными.  —  М.:  Мир,  1972.  —  414  с.

4.Лурье  К.А.  Оптимальное  управление  в  задачах  математической  физики.  М.:  Наука,  1975.  —  480  с.

5.Сиразетдинов  Т.К.  Оптимизация  систем  с  распределенными  параметрами.  —  М.:  Наука,  1977  —  480  с.