Статья опубликована в рамках: VI Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 27 мая 2013 г.)
Наука: Информационные технологии
Секция: Автоматизация и управление технологическими процессами и производствами
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ИДЕНТИФИКАЦИЯ НАПОРНОЙ ХАРАКТЕРИСТИКИ НАСОСА
Бакаляр Николай Владимирович
бакалавр Московского физико-техническогоинститута (Государственного университета), г. Долгопрудный
Тмур Антон Борисович
главный специалист ООО «Интэком», г. Москва
Юрченко Сергей Михайлович
канд. физ.-мат. наук, Технический директор ООО «Интэком», г. Москва
E-mail: kolyan89@gmail.com
Трубопроводный транспорт нефти в настоящее время является самым дешёвым видом транспорта энергоресурсов. Однако при длительном использовании трубопровод изнашивается, что может привести к нежелательным авариям и разливам нефти. Такие аварии наносят значимый ущерб окружающей среде, а ликвидация их последствий является весьма дорогостоящим процессом.
В связи с этим широкое развитие и применение получило математическое моделирование в сфере трубопроводного транспорта. Сейчас модели применяются при решении различных задач: при расчёте режимов работы трубопровода, при создании систем обнаружения утечек, при расчёте нестационарных процессов, возникающих при переходе с режима на режим и т. д.
Одной из частей задачи моделирования трубопроводной системы является моделирование работы насоса. При моделировании работы насоса очень важно использование напорной характеристики (зависимость напора H от подачи (расхода) Q), которая максимально приближена к реальной. В связи с этим возникает задача идентификации напорной характеристики на основе исторических данных о параметрах работы насоса.
Ограничимся наиболее простым режимом работы насоса — без кавитационных явлений в проточной части. Кавитация на входе в насос сказывается на собственной частоте колебаний жидкости в тракте перед насосом, а иногда и на коэффициенте усиления насоса, т. е. на отношении амплитуды колебаний давления на выходе из насоса к амплитуде на его входе.
При формировании математической модели течения жидкости в насосе пренебрегаем сжимаемостью жидкости и податливостью стенок насоса, т. к. скорость жидкости в проточной части достаточно велика. А также ограничимся наиболее простым режимом работы насоса — без кавитационных явлений в проточной части. При таких предположениях перепад давлений, создаваемый насосом, описывается многочленом:
 ,(1)
,(1)

Рисунок 1. Схема центробежного насоса
где:![]() ,
, ![]() ,
, ![]() — коэффициенты напорной характеристики насоса,
— коэффициенты напорной характеристики насоса,
Q – объемный расход через насос,
N — текущее число оборотов насоса в минуту,
![]() ,
, ![]() — давление до насоса и за насосом соответственно.
— давление до насоса и за насосом соответственно.
В нашей же работе мы предположим, что напорная характеристика описывается следующим многочленом третьей степени:
![]() , (2)
, (2)
где: H — напор, создаваемый насосом в![]() ,
,
Q — расход в ![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() — постоянные коэффициенты.
— постоянные коэффициенты.

Рисунок 2. Напорная характеристика насоса
Это сделано, потому что напорная характеристика насоса, для которого получены экспериментальные данные, имеет вид, представленный на Рисунке 2. Из рисунка видно, что график напорной характеристики имеет точку перегиба, в которой вторая производная меняет знак. Для аппроксимации такой функции необходимо использовать многочлен как минимум третьей степени.
Исходя из предположений [4], можно получить корректировку напорной характеристики, имея единичное измерение ![]() . Сначала предположим, что напорная характеристика изменена только за счет изменения диаметра колеса насоса и мы имеем только одно измерение, полученное при измененной характеристике. При таком предположении [5] напорная характеристика может измениться следующим образом:
. Сначала предположим, что напорная характеристика изменена только за счет изменения диаметра колеса насоса и мы имеем только одно измерение, полученное при измененной характеристике. При таком предположении [5] напорная характеристика может измениться следующим образом:
 (3)
(3)
Здесь коэффициент k варьируется в зависимости от того, насколько изменился диаметр.
Тогда,
![]() (4)
(4)
и коэффициент k есть решение нелинейного уравнения третьей степени:
![]() (5)
(5)
Рассчитав коэффициент k, можно получить коэффициенты новой напорной характеристики, основанной только на одном измерении
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
Здесь верхний индекс initial означает коэффициенты заводской напорной характеристики, считающиеся известными.
В случае большого числа измерений для каждого i-го измерения имеем ошибку:
![]() (10)
(10)
Тогда, для определения k воспользуемся методом наименьших квадратов. Необходимо минимизировать следующий функционал:
![]() (11)
(11)
Минимум такого функционала находится путем приравнивания нулю следующей производной:
![]() (12)
(12)
После взятия производной, раскрытия скобок и замены величин ![]() и
и ![]() на соответствующие им безразмерные:
на соответствующие им безразмерные:
 ;
; ![]() (13)
(13)
Получаем нелинейное уравнение
![]() (14)
(14)
с коэффициентами
![]() (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
![]() (19)
(19)
![]() (20)
(20)
Введем следующие величины
![]()
![]()
![]()
![]()

 (21)
(21)







Тогда, используя еще одну замену ![]() , решаем нелинейное уравнение относительно
, решаем нелинейное уравнение относительно ![]() :
:
![]() , (22)
, (22)
с коэффициентами
![]() (23)
(23)
![]() (24)
(24)
![]() (25)
(25)
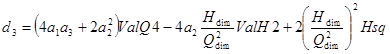 (26)
(26)
 (27)
(27)
![]() (28)
(28)
Решив полученное нелинейное уравнение, находим ![]() . Затем находим
. Затем находим ![]() и пересчитываем коэффициенты напорной характеристики (получаем первое приближение по всем полученным данным):
и пересчитываем коэффициенты напорной характеристики (получаем первое приближение по всем полученным данным):
![]() (29)
(29)
![]() (30)
(30)
![]() (31)
(31)
![]() (32)
(32)
Верхний индекс у коэффициентова означает: initial — заводская напорная характеристика. Далее, мы скорректируем полученное первое приближение, пользуясь Методом внутренней точки.
На данном этапе мы вводим ограничения на условия нахождения коэффициентов. Во-первых, производная функции напорной характеристики должна быть не положительной. Это необходимо для недопущения неустойчивости системы. Т. к. если допустить, что напорная характеристика может возрастать, то при увеличении напора, мы увеличиваем и расход. Исходя из этого возможно увеличение расхода до бесконечности, при увеличении напора, что физически невозможно. Чтобы устранить такую возможность введем одномерную сетку ![]() ,
,![]() с шагом
с шагом ![]() и такую, что точка
и такую, что точка ![]() совпадает с точкой пересечения напорной характеристики и оси абсцисс. В каждой точке сетки посчитаем первую производную. Она равна:
совпадает с точкой пересечения напорной характеристики и оси абсцисс. В каждой точке сетки посчитаем первую производную. Она равна:
 (33)
(33)
Каждая такая производная должна быть меньше либо равна нулю. Получаем первую часть матрицы ограничений:
 (34)
(34)
Вторая часть матрицы ограничений — это ограничения, вводимые на концах напорной характеристики. Такие ограничения нужны, потому что идентификация происходит для данных, которые лежат в рабочей зоне насоса. При этом часть идентифицированной характеристики, которая соответствует нерабочей зоне насоса, может сильно расходиться с реальной. Чтобы этого не происходило, и накладываются ограничения на концы напорной характеристики. Для удобства, пусть каждое ограничение выражается следующим образом: значение напора, рассчитываемое по напорной характеристике в точке![]() не больше
не больше![]() , если
, если ![]() , и не меньше
, и не меньше![]() , если
, если ![]() . Таким образом, каждое ограничение есть тройка чисел:
. Таким образом, каждое ограничение есть тройка чисел: ![]() ,
, ![]() ,
, ![]() .
.
Получаем вторую часть матрицы ограничений. Вся система ограничений имеет следующий вид:
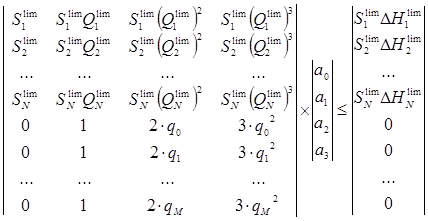 (35)
(35)
В результате имеем задачу условной оптимизации вида:
![]() ,
,
при
 (36)
(36)
Перепишем в следующем вид:
![]() ,
, ![]() . (37)
. (37)
На ее основе строится задача безусловной минимизации:
![]() ,
,![]() , (38)
, (38)
где: ![]() — расширенная функция,
— расширенная функция,
![]() — штрафная функция,
— штрафная функция,
![]() — штрафной параметр.
— штрафной параметр.
Задача условной минимизации ![]() заменяется последовательностью задач безусловной минимизации
заменяется последовательностью задач безусловной минимизации ![]() при t=1,2... При этом, исходя из заданной начальной точки
при t=1,2... При этом, исходя из заданной начальной точки ![]() , находится последовательность точек
, находится последовательность точек ![]() ,
,![]() ,..., сходящаяся при определенных условиях к решению
,..., сходящаяся при определенных условиях к решению ![]() исходной задачи. При минимизации расширенной функции
исходной задачи. При минимизации расширенной функции ![]() , t=1,2..., исходной (начальной) точкой является
, t=1,2..., исходной (начальной) точкой является ![]() , а решение задачи безусловной минимизации
, а решение задачи безусловной минимизации ![]() определяет точку
определяет точку ![]() .
.
В качестве внутренней штрафной функции мы будем использовать логарифмическую штрафную функцию:
 . (39)
. (39)
Для вычисления ![]() используется рекуррентное соотношение
используется рекуррентное соотношение
![]() , t=1,2,…, (40)
, t=1,2,…, (40)
где![]() (
(![]() ),
), ![]() (
(![]() ).
).
При этом на каждом шаге алгоритма, чтобы минимизировать функционал ![]() мы будем применять хорошо известный метод Ньютона.
мы будем применять хорошо известный метод Ньютона.
Далее продемонстрированы результаты расчетов. Физические параметры исследуемой системы предоставлены ООО «Интеком». Коэффициенты заводской напорной характеристики для насоса:
![]() (41)
(41)
![]() (42)
(42)
![]() (43)
(43)
![]() (44)
(44)
Во-первых, продемонстрируем, что по одной точке, согласно теории, наша модель определяет новые коэффициенты (n=1).

Рисунок 3. Идентификация по 1 точке
Красная линия — заводская характеристика. Синяя линия — результат идентификации. Черная точка — данные. Ось абсцисс — Расход в ![]() . Ось ординат — Напор в
. Ось ординат — Напор в![]() .
.
Возьмем 10 точек (n=10).

Рисунок 4. Идентификация по 10 точкам
Красная линия — заводская характеристика. Черная линия — результат идентификации. Синие точки — данные. Ось абсцисс — Расход в ![]() . Ось ординат — Напор в
. Ось ординат — Напор в![]() .
.

Рисунок 5. Идентификация по 10 точкам
Красная линия — заводская характеристика. Черная линия — результат идентификации. Синие точки — данные. Ось абсцисс — Расход в ![]() . Ось ординат — Напор в
. Ось ординат — Напор в![]() .
.
В конце хотелось бы подвести итог проделанной работе. Мы получили следующие результаты:
1. Построен эффективный метод, позволяющий проводить идентификацию напорной характеристики насоса, который внедрен и успешно применяется на нефтепроводе ВСТО-2.
2. Данный метод позволяет учитывать кубическую форму напорной характеристики, а также накладывать ограничения в форме неравенств, как на саму функцию ![]() , так и на ее производную.
, так и на ее производную.
3. Перспективным направлением развития данной работы является получение аналогичных оценок погрешности для идентификации эффективных диаметров, расходных характеристик заслонок регуляторов.
Список литературы:
1.Вайншток С.М. Трубопроводный транспорт нефти. т. 1 — М.: Недра, 2002 г. — 407 с.
2.Гликман Б.Ф. Автоматическое регулирование жидкостных ракетных двигателей — 2-е изд., перераб. и доп. — М.: Машиностроение. 1989 г. — 296 с.
3.Гроп Д. Методы идентификации систем — М.: Мир, 1979 г. — 302 с.
4.Кузьминский Ю.Г., Шилько С.В., Вьюн В.И. Расчет гидравлических характеристик путем идентификации моделей насосных агрегатов и перекачивающих станций магистральных нефтепроводов //Механика машин, механизмов и материалов. 2008 г. — № 3 — с. 58—63.
5.Лурье М.И. Математические модели в транспорте нефти и газа — М.: РГУ нефти и газа им. Губкина, 2001 г.
6.Поляк Б.Т. Введение в оптимизацию — М.: Наука, 1983 г. — 384 с.
7.Харчистов Б.Ф. Методы оптимизации: Учебное пособие — Таганрог: Изд-во ТРТУ, 2004 г. — 140 с.
дипломов


Комментарии (1)
Оставить комментарий