Статья опубликована в рамках: XV Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 05 февраля 2014 г.)
Наука: Математика
Секция: Дифференциальные уравнения, динамические системы и оптимальное управление
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
АНАЛИЗ МНОЖЕСТВА ДОСТИЖИМОСТИ НЕЛИНЕЙНЫХ УПРАВЛЯЕМЫХ СИСТЕМ
Екимов Александр Валерьевич
канд. физ.-мат. наук, доцент, Санкт-Петербургский государственный университет, Россия, г. Санкт-Петербург
E-mail: alex.ekimov@mail.ru
THE ANALYSIS OF THE ATTAINABILITY SET OF NONLINEAR CONTROLLED SYSTEMS
Alexander Ekimov
candidate of physico-mathematical sciences, associate professor of Saint-Petersburg State University, Russia, Saint-Petersburg
E-mail: alex.ekimov@mail.ru
АННОТАЦИЯ
Рассмотрена проблема анализа множества достижимости нелинейных управляемых систем. Получены достаточные условия ограниченности интегральной воронки
ABSTRACT
The attainability set analysis problem for nonlinear controlled systems are considered. The sufficient conditions of boundedness of the integral vortex are obtained.
Ключевые слова: управление; устойчивость; множество достижимости; интегральная воронка.
Keywords: control; stability; attainability set; integral vortex.
Введение. Множество достижимости является фундаментальной характеристикой управляемой системы. Анализ множества достижимости и построение его оценок, как отмечено в [3], существенно облегчает решение целого ряда задач математической теории управления. Наиболее полный анализ множества достижимости проведен для линейных управляемых систем. При анализе нелинейных управляемых систем часто пользуются линейными аппроксимациями.
Основные понятия. Рассмотрим нелинейную управляемую систему где ![]() непрерывная и ограниченная при
непрерывная и ограниченная при ![]() матрица, вектор-функция
матрица, вектор-функция ![]() также непрерывна по своим аргументам в области D
также непрерывна по своим аргументам в области D![]() . Допустимыми считаем скалярные управления
. Допустимыми считаем скалярные управления ![]() , которые являются кусочно-непрерывными функциями при
, которые являются кусочно-непрерывными функциями при ![]() . Множество допустимых управлений будем обозначать
. Множество допустимых управлений будем обозначать ![]() .
.
Определение [3]. Множеством достижимости ![]() системы (1) называется совокупность концов
системы (1) называется совокупность концов ![]() всех траекторий этой системы, начинающихся в момент
всех траекторий этой системы, начинающихся в момент ![]() в точке
в точке ![]()
Определение [3]. Множество ![]() называется интегральной воронкой системы (1).
называется интегральной воронкой системы (1).
В данной работе рассматривается вопрос об ограниченности интегральной воронки ![]() нелинейной управляемой системы (1).
нелинейной управляемой системы (1).
Определение. Множество достижимости ![]() будем считать ограниченным, если оно может быть погружено в сферу конечного радиуса.
будем считать ограниченным, если оно может быть погружено в сферу конечного радиуса.
Наряду с системой ![]() рассмотрим линейную однородную систему
рассмотрим линейную однородную систему
![]()
Определение [1]. Система ![]() называется экспоненциально устойчивой, если для любого ее решения
называется экспоненциально устойчивой, если для любого ее решения ![]() справедливо неравенство
справедливо неравенство
![]()
где: ![]() положительные постоянные, не зависящие от выбора решения.
положительные постоянные, не зависящие от выбора решения.
Теоретический анализ. В дальнейшем будем использовать следующую лемму об интегральных неравенствах.
Лемма Гронуолла-Беллмана ![]() . Пусть
. Пусть ![]() и
и ![]() непрерывны при
непрерывны при ![]() причем для любого
причем для любого ![]() выполнено неравенство
выполнено неравенство

где: ![]() положительная постоянная. В таком случае при
положительная постоянная. В таком случае при ![]() имеем
имеем
![]()
Предположим, что множество допустимых управлений имеет вид
![]() .
.
Теорема 1. Для того, чтобы интегральная воронка ![]() системы (1) была ограничена для любого
системы (1) была ограничена для любого ![]() , достаточно, чтобы
, достаточно, чтобы
1. Система ![]() была экспоненциально устойчивой;
была экспоненциально устойчивой;
2. ![]() где
где ![]() положительная постоянная;
положительная постоянная;
3. ![]() где
где ![]() положительная постоянная.
положительная постоянная.
Доказательство: Обозначим через ![]() нормированную при
нормированную при ![]() фундаментальную матрицу системы
фундаментальную матрицу системы ![]() . Для матрицы Коши
. Для матрицы Коши ![]() в силу экспоненциальной устойчивости этой системы справедлива оценка
в силу экспоненциальной устойчивости этой системы справедлива оценка
![]()
Интегральное уравнение, эквивалентное системе (1), в терминах матрицы Коши имеет вид

Переходя к оценке по норме с учетом ![]() получим
получим

Преобразуем полученное неравенство следующим образом:

Далее воспользуемся условиями 2,3 теоремы 1.

Поскольку ![]() получаем неравенство
получаем неравенство

Далее воспользуемся леммой Гронуолла-Беллмана.
![]()
Таким образом, интегральная воронка ![]() системы (1) ограничена для любого
системы (1) ограничена для любого ![]()
Теорема доказана .
Для обобщения теоремы 1 воспользуемся следующей леммой об интегральных неравенствах.
Лемма Бихари ![]() . Пусть
. Пусть ![]() и
и ![]() непрерывны при
непрерывны при ![]() причем для любого
причем для любого ![]() выполнено неравенство
выполнено неравенство

где: ![]() положительная постоянная,
положительная постоянная, ![]() . В таком случае при
. В таком случае при ![]() имеем
имеем
![]() если
если ![]()
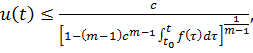 если
если ![]() и
и ![]() .
.
Теорема 2. Для того, чтобы интегральная воронка ![]() системы (1) была ограничена для любого
системы (1) была ограничена для любого ![]() , достаточно, чтобы
, достаточно, чтобы
1. Система ![]() была экспоненциально устойчивой;
была экспоненциально устойчивой;
2. ![]() где
где ![]() положительная постоянная,
положительная постоянная, ![]() ;
;
3. ![]() где
где ![]() положительная постоянная.
положительная постоянная.
При ![]() ограниченность интегральной воронки имеет место при определенном соотношении параметров
ограниченность интегральной воронки имеет место при определенном соотношении параметров ![]()
Доказательство: Действуя по аналогии с доказательством теоремы 1, получим следующее неравенство для нормы решения
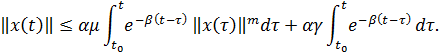
При ![]() в соответствии с леммой Бихари
в соответствии с леммой Бихари
 .
.
Очевидно, что в данном случае ограниченность интегральной воронки имеет место при любом соотношении параметров ![]()
При ![]() оценки будут корректными лишь в случае
оценки будут корректными лишь в случае
![]() или
или ![]()
Таким образом, ограниченность интегральной воронки в данном случае имеет место при достаточно малых ![]() и достаточно большом
и достаточно большом ![]() Для нормы решения получим оценку
Для нормы решения получим оценку
 .
.
Теорема доказана .
Замечание. Для доказательства теорем 1,2 может быть использован второй метод Ляпунова ![]() . В качестве функций Ляпунова можно выбрать квадратичные формы в соответствии с теоремой о необходимых и достаточных условиях экспоненциальной устойчивости системы
. В качестве функций Ляпунова можно выбрать квадратичные формы в соответствии с теоремой о необходимых и достаточных условиях экспоненциальной устойчивости системы ![]() сформулированных в работе
сформулированных в работе ![]() Данный подход продемонстрирован в работе автора
Данный подход продемонстрирован в работе автора ![]() .
.
Список литературы :
1.Демидович Б.П. Лекции по математической теории устойчивости. М., Наука, 1967, — 472 с.
2.Зубов В.И. Лекции по теории управления. М., Наука, 1975, — 495 с.
3.Черноусько Ф.Л. Оценивание фазового состояния динамических систем. М., Наука, 1988, — 320 с.
4.Ekimov A.V. The estimate of the integral vortex of controlled systems by the Lyapunov functions method. // Preprints of the eleventh IFAC international workshop «Control applications of optimization», SPb., 2000, — p. 106—110.
дипломов


Оставить комментарий