КВАТЕРНИОНЫ  КАК  ВЕЩЕСТВЕННЫЕ  МАТРИЦЫ  СПЕЦИАЛЬНОГО  ВИДА  И  ИХ  РОЛЬ  В  ОПРЕДЕЛЕНИИ  СКАЛЯРНОГО  И  ВЕКТОРНОГО  ПРОИЗВЕДЕНИЯ  ВЕКТОРОВ

Свиркина  Лариса  Анатольевна

канд.  физ.-мат.  наук,  доцент  Санкт-Петербургского  государственного  университета,  РФ,  г.  Санкт-Петербург

E-mail:  lara_a@mail.ru

Хитров  Геннадий  Михайлович

доцент,  канд.  физ.-мат.  наук,  доцент  Санкт-Петербургского  государственного  университета,  РФ,  г.  Санкт-Петербург

E-mail: 

QUATERNIONS  AS  REAL  MATRICES  OF  THE  SPECIAL  KIND  AND  THEIR  ROLE  IN  DEFINITION  OF  SCALAR  AND  VECTOR  PRODUCT  OF  VECTORS

Larisa  Svirkina

candidate  of  physical  and  mathematical  sciences,  associate  professor  of  St.  Petersburg  State  University,  Russia,  St.  Petersburg

Gennady  Khitrov

associate  professor,  candidate  of  physical  and  mathematical  sciences,  associate  professor  of  St.  Petersburg  State  University,  Russia,  St.  Petersburg

АННОТАЦИЯ

Дано  современное  компактное  изложение  алгебры  кватернионов.  Доказаны  основные  свойства  этой  алгебраической  структуры.  Приведена  геометрическая  интерпретация  векторной  части  кватерниона,  благодаря  которой  кватернионы  нашли  широкое  применение,  как  в  описании  управляемых  движений  космических  аппаратов,  так  и  в  компьютерных  играх. 

ABSTRACT

The  modern  compact  treatment  of  quaternion  algebra  is  presented.  The  main  properties  of  this  algebraic  structure  are  proved.  Because  of  the  geometrical  interpretation  of  their  imaginary  part,  quaternions  are  widely  used  both  in  the  description  of  controlled  motion  of  spacecrafts  and  computer  games.

Ключевые  слова:  матрицы;  алгебраические  структуры;  кватернионы.

Keywords:  matrices;  algebraic  structures;  quaternions.

Введение.  Широкое  использование  кватернионов  в  различных  областях  науки  [1,  2,  4,  6]  и  компьютерных  технологиях  [5,  7]  все  настоятельнее  требует  изучения  кватернионов  в  начальном  курсе  алгебры.  В  статье  показывается,  что  матричный  подход  к  введению  комплексных  чисел  может  быть  использован  и  для  введения  кватернионов.  При  этом  большая  часть  свойств  кватернионов  вытекает  из  соответствующих  свойств  квадратных  вещественных  матриц.  Поскольку  некоторые  курсы  алгебры  начинаются  с  изучения  линейных  систем  и  матриц,  то  кватернионы  могут  изучаться  уже  в  первом  семестре  первого  курса.  По  сути,  матричному  подходу  к  введению  кватернионов  и  строгому  доказательству  некоторых  основных  свойств  кватернионов  и  посвящена  данная  работа.  Более  того,  статья  объясняет,  как  из  кватернионов  появились  скалярное  и  векторное  произведения  векторов  трехмерного  пространства.

Из  соображений  разумной  экономии  в  статье  не  рассматривается  история  появления  и  изучения  кватернионов,  поскольку  сегодня  ответы  на  эти  вопросы  легко  найти  в  Интернете.  Отметим  только,  что  существует  несколько  подходов  к  объяснению  появления  и  обоснования  кватернионов.  Например,  кватернионы  иногда  рассматривают  как  обобщение  комплексных  чисел,  точнее  как  числа  с  тремя  «мнимыми  единицами»,  с  заданными  законами  перекрестных  произведений  мнимых  единиц  и  умножений  этих  единиц  самих  на  себя.  Поэтому  кватернионы  относят  к  категории  так  называемых  «гиперкомплексных  чисел»  [3].  При  таком  подходе  к  определению  кватернионов  возникают  определенные  технические  трудности,  особенно  при  доказательстве  свойств  умножения  кватернионов.  Гораздо  проще  определить  кватернионы  как  вещественные  квадратные  матрицы  четвертого  порядка  специального  вида.  Так  как  множество  вещественных  квадратных  матриц  относительно  операций  сложения,  умножения  и  умножения  матриц  на  вещественные  числа  образуют  алгебраическую  структуру,  называемую  алгеброй  (кольцо  со  структурой  векторного  пространства)  над  полем  вещественных  чисел,  то,  определяя  кватернионы  как  матрицы,  мы  знаем,  что  они  обладают  целым  набором  свойств,  характеризующих  алгебру  квадратных  матриц.  Поэтому  остается  рассмотреть  только  специфику  кватернионов,  вытекающую  из  специфики  определяющих  их  матриц.  Мы  предполагаем,  что  читатель  знаком  с  основами  линейной  алгебры  и  знает  основные  свойства  сложения  и  умножения  матриц,  поэтому  чтение  данной  статьи  не  вызовет  больших  затруднений. 

Чтобы  показать,  что  и  при  «матричном»  введении  кватернионов,  кватернионы  остаются  обобщением  комплексных  чисел,  сделаем  замечание  о  «матричном»  введении  комплексных  чисел.

Если  рассмотреть  множество  квадратных  матриц  второго  порядка  вида  ,  где  a  и  b  произвольные  вещественные  числа,  то  несложно  показать,  что  это  множество  относительно  операций  сложения  и  умножения  образует  поле,  изоморфное  известному  полю  комплексных  чисел.  Причем,  с  учетом  свойств  умножения  матриц  на  вещественные  числа,  мы  должны  отметить,  что  в  этом  случае  имеем  дело  с  алгеброй  над  полем  вещественных  чисел.

Делается  это  следующим  образом.  Указанная  матрица  представляется  в  виде:

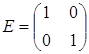,  где  ,  а  .

Поскольку  ,    и  ,  то  перемножение  двучленов  коммутативно,  т.  е.  .  Следовательно,  умножение  матриц  вида    коммутативно.  Далее,  если  a  и  b  одновременно  не  равны  нулю,  то  её  определитель  отличен  от  нуля,  и,  следовательно,  для  любой  ненулевой  матрицы  указанного  вида  существует  обратная.  Теперь  уже  несложно  видеть,  что  множество  матриц  указанного  вида  относительно  операции  сложения  образует  коммутативную  группу.  Без  нулевой  матрицы  упомянутое  множество  образует  коммутативную  группу  относительно  умножения.  Операции  сложения  и  умножения  матриц  связаны  законом  дистрибутивности  и,  следовательно,  множество  матриц  с  вещественными  элементами  вида    образует  поле.  Это  поле  изоморфно  полю  комплексных  чисел  C  вида  ,  где  .  Изоморфизм  устанавливается  естественным  взаимно  однозначным  отображением    в  ,  сохраняющим  операции.  Поскольку  множество  матриц  указанного  вида  является  алгеброй  над  полем  вещественных  чисел,  то  очевидно,  что  и  поле  комплексных  чисел  C  является  алгеброй  над  полем  вещественных  чисел.

Алгебра  кватернионов.  Рассмотрим  множество  вещественных  матриц  четвертого  порядка  вида:

,                                     (1)

где  a,  b,  c  и  d  вещественные  числа.  Введя  обозначения 

,  ,  ,

                                     (2)

мы  можем  записать  произвольную  матрицу  (1)  в  виде  линейной  комбинации  матриц:  E,  I.  J  и  K.  То  есть 

               (3)

Очевидно,  что  матрицы  E,  I.  J  и  K  линейно  независимы,  поскольку  их  ненулевые  элементы  расположены  на  разных  местах  квадратной  матрицы  четвертого  порядка.  Поскольку  линейные  комбинации  линейных  комбинаций  этих  матриц  будут  снова  линейными  комбинациями  этих  же  матриц,  то  указанное  множество  линейных  комбинаций,  которое  в  дальнейшем  будем  обозначать  через  H,  образует  четырехмерное  подпространство  в  16-мерном  пространстве  вещественных  квадратных  матриц  4-го  порядка. 

Покажем,  что  множество  H  замкнуто  относительно  операции  матричного  умножения  элементов.  Чтобы  облегчить  себе  работу  по  проверке  этого  утверждения,  рассмотрим  блочное  разбиение  матриц  E,  I.  J  и  K  на  четыре  равных  по  размеру  блока.  При  этом  мы  используем  введенные  ранее  обозначения  базисных  векторов  E  и    алгебры  C.  Выпишем  блочный  вид  матриц  E,  I.  J  и  K: 

             (4)

Сделаем  замечание  относительно  обозначений:  здесь  через  E  обозначается  как  матрица  4-го,  так  и  матрица  2-го  порядка.  Поскольку  порядок  матрицы  E  определяется  её  местом  в  матричном  выражении,  то  надеемся,  что  это  не  приведет  к  недоразумениям. 

Так  как  умножение  линейных  комбинаций  сводится  к  умножению  и  сложению  коэффициентов  (чисел)  и  умножению  образующих  этих  линейных  комбинаций  между  собой,  то  сосредоточимся  вначале  на  этих  действиях.  Поскольку  умножение  и  сложение  вещественных  чисел  —  известные  операции,  то  уделим  основное  внимание  умножению  образующих  между  собой.  В  силу  свойств  единичной  матрицы  имеем:  ,  ,  ,  .  При  вычислении  попарных  произведений  IJ,  JI,  IK,  KI,  JK,  KJ,  II,  JJ,  KK  удобно  воспользоваться  блочным  представлением  матриц  I,  J,  K.  Опуская  несложные  вычисления,  выпишем  полученные  результаты:  .  С  учетом  этих  равенств  теперь  несложно  выписать  произведение  двух  произвольных  линейных  комбинаций  из  H.  Ориентируясь  на  дальнейшее,  выпишем  произвольные  линейные  комбинации  в  виде:    и  .  Перемножая  эти  линейные  комбинации,  получим: 

         (5)

Итак,  показано,  что  результат  операция  умножения  элементов  из  H,  является  элементом  из  H.  То  есть  операция  умножения  в  H  замкнута.  Поскольку  проверка  свойств  дистрибутивности  не  представляет  труда  и  доказано,  что  эти  свойства  выполняются,  то  можно  утверждать,  что  H  является  кольцом.  Из  свойств  умножения  матриц  следует,  что  это  кольцо  ассоциативное  и  с  единицей.  Из  свойств  попарных  произведений  IJ,  JI,  IK,  KI,  JK,  KJ,  следует,  что  это  кольцо  некоммутативное.  Рассмотрим  еще  одно  свойство  умножения  элементов  из  H.  Именно,  найдем  произведение 

  (6)

Отсюда  следует,  что  для  ненулевого  элемента  из  H  (очевидно,  что  элемент  из  H  равен  0  тогда  и  только  тогда,  когда  )  существует  обратный  элемент.  Так  для  ненулевого  элемента    обратным  будет  элемент

.

То  есть,

                             (7)

Из  (6)  следует,  что  .  Откуда 

                                       (8)

Сравнивая  теперь  (7)  с  формулой  для  обратной  матрицы  к  матрице  A

,

где:    —  присоединенная  (союзная)  матрица  к  матрице  A,  получим,  что

                                     (9)

Назовем  величину  ,  равную  арифметическому  значению  корня,  модулем  элемента  (матрицы)  A  из  H.  Будем  обозначать  модуль  элемента  (матрицы)  A  как  ,  т.  е.  положим  .  Используя  обозначение  модуля,  мы  можем  переписать  формулу  (6)  в  виде:  .  Из  (5)  и  (6)  теперь  следует,  что 

.

Откуда  следует,  что  ,  т.  е.  модуль  произведения  двух  элементов  из  H  равен  произведению  модулей  этих  элементов.  Соотношение  для  квадратов  модулей,  записанное  в  развернутом  виде  и  в  обратном  порядке,  носит  название  тождества  Эйлера.  То  есть, 

                                   (10)

тождество  Эйлера.

Определение.  Ассоциативное  кольцо  с  единицей,  у  которого  для  каждого  ненулевого  элемента  существует  обратный,  называется  телом.

Из  определений  тела  и  поля  следует,  что  каждое  поле  является  телом.  Однако  пример  тела  H  показывает,  что  не  каждое  тело  является  полем. 

Выше  нами  показано,  что  H  является  алгеброй,  в  которой  кольцо  имеет  структуру  тела.  Как  и  в  случае  с  алгеброй  C  для  алгебры  H  в  практике  нашло  применение  не  матричное  выражение  элементов  этой  алгебры,  а  изоморфное  отображение  этой  алгебры  в  «числа  вида»  ,  которые  называются  кватернионами.  То  есть  каждому  элементу    алгебры  H  мы  сопоставляем  кватернион  .  Единицы  i,  j,  k  —  называются  (по  аналогии  с  комплексными  числами)  мнимыми  единицами.  Часть  кватерниона  —  число  ,  по  аналогии  с  комплексными  числами,  можно  было  бы  называть  вещественной  частью  кватерниона,  а  упорядоченную  тройку    —  мнимой  частью  кватерниона.  Однако  это  неудобно,  поскольку  приходится  отрывать  уже  три  коэффициента  от  мнимых  единиц.  При  делении  кватерниона  на  части,  за  частями  закрепились  совсем  другие  названия,  оправданные  дальнейшей  интерпретацией.  Так  число    называется  скалярной  частью  кватерниона,  а  часть  кватерниона    называется  векторной  частью  кватерниона.

На  множестве  кватернионов  определены  равенство  (два  кватерниона  равны,  когда  равны  их  скалярные  и  векторные  части),  сложение,  умножение  на  вещественные  числа  и  умножение  кватернионов.  Перемножение  кватернионов  выражается  в  перемножении  и  сложении  коэффициентов  (вещественных  чисел  )  и  перемножении  мнимых  единиц,  подчиненных  правилам:  .  Причем  перемножение  осуществляется  так,  как  учили  в  школе  перемножать  скобку  на  скобку,  но  с  учетом  свойств  перемножения  мнимых  единиц.  При  этом  подразумевается,  что  вещественные  числа  коммутируют  (перестановочны)  как  между  собой,  так  и  с  мнимыми  единицами.  Очевидно,  с  учетом  сказанного  о  сложении  и  произведении  кватернионов,  что  отображение    в    не  только  взаимнооднозначно,  но  и  сохраняет  операции.  Следовательно,  это  отображение  является  изоморфизмом. 

Очевидно,  что  для  кватернионов  имеем  полный  аналог  формулы  (5):

     (11)

Как  и  для  комплексных  чисел,  для  кватернионов  вводится  понятие  сопряженного  кватерниона.  Кватернион    будем  называть  сопряженным  кватерниону  .  Очевидно,  что  сопряженным  сумме  кватернионов    и    будет  сумма  сопряженных,  т.е.  .  Сопряженным  произведению  –  будет  произведение  сопряженных,  взятых  в  обратном  порядке,  т.е.    (напоминаем  связь  сопряжения  с  транспонированием  матриц).

Для  кватерниона,  как  и  для  комплексного  числа,  вводится  понятие  модуля.  Именно,  величина    называется  модулем  кватерниона  .  Модуль  кватерниона    будем  обозначать,  как  .  Несложно  непосредственно  посчитать  (или  сослаться  на  соответствующую  связь  с  матрицами),  что  .  Теперь,  как  и  для  соответствующих  матриц,  доказывается  тождество  Эйлера  (10),  и  утверждение,  что  модуль  произведения  кватернионов  равен  произведению  их  модулей,  т.е.  .

Обратным  для  кватерниона    будет  кватернион  .

В  дальнейшем,  через  H  мы  будем  обозначать  уже  не  четырехмерное  подпространство  вещественных  квадратных  матриц  четвертого  порядка  специального  (указанного  выше)  вида,  а  множество  кватернионов.  Это  позволит  нам  сохранить  в  памяти  связь  кватернионов  с  матрицами  и  при  необходимости  пользоваться  ею.

Трехмерное  подпространство    четырехмерного  пространства  .  Рассмотрим  множество  линейных  комбинаций  с  вещественными  коэффициентами  вида  .  Обозначим  это  множество  через  .  Очевидно,  что    образует  трехмерное  подпространство  в  ,  поэтому  элементы  этого  подпространства,  будем  называть  векторами.  Введем  в    операцию  умножения  векторов,  определяемую  правилом:  для  любых    положим

,                                           (12)

где:  —  операция  умножения  в  .  Из  (11)  следует,  что  .  Действительно,  положив  в  (11)  ,  получим:

Следовательно,

,  т.е.  .

Перейдем  к  геометрической  интерпретации  подпространства  .  Для  этого  отождествим  мнимые  единицы  i,  j,k  с  ортами  декартовой  системы  координат  i,  j,  k  (правая  тройка).  Тогда  линейной  комбинации  мнимых  единиц    будет  соответствовать  линейная  комбинация  ортов  ,  т.е.  вектор.  Таким  образом,  каждому  кватерниону    мы  сопоставляем  вектор  .  Далее,  поскольку  ,  то,  используя  введенное  в  (12)  обозначение  для  произведения  элементов  из  ,  получим  ,  ,  .

Не  впадая  в  противоречие  с  определением  произведения    для  кватернионов  из  ,  введем  векторное  произведение  векторов    в  трехмерном  пространстве  с  декартовой  системой  координат  и  ортами  i,  j,  k,  задав  векторное  произведение  формулой:

    (13)

Из  (13)  для  ортов  i,  j,  k  декартовой  системы  координат  следует:  ,  ,  .

Перечислим  теперь  свойства  векторного  произведения,  вытекающие  из  этого  определения.

Во-первых,  векторное  произведение  замкнуто  на  множестве  векторов  (очевидным  образом  следует  из  определения). 

Во-вторых,  выполняются  свойства  дистрибутивности.  Действительно, 

,

.

Таким  образом,  трехмерное  вещественное  пространство  векторов  относительно  операций  сложения  и  векторного  умножения  векторов  образует  структуру  кольца. 

Это  кольцо  не  ассоциативное.  Например,  поскольку  ,  а  ,  то  .

Это  кольцо  не  коммутативное,  ибо  ,  и  в  нём  нет  «единицы».

Мы  не  будем  заниматься  дальнейшей  геометрической  интерпретацией  векторного  произведения  векторов,  поскольку  это  предмет  аналитической  геометрии,  где  векторное  произведение  изучается  более  детально. 

Отметим  ещё  одно  умножение  элементов  из    и  соответствующее  ему  умножение  трехмерных  векторов.  Для  чего  рассмотрим  произведение  в  ,  заданное  формулой  (правилом):

,

где  ,  а    —  умножение  кватернионов  в  .  Соответствующее  произведение  векторов    и    задаётся  формулой    и  называется  скалярным  произведением  векторов. 

Перечислим  некоторые  свойства  скалярного  произведения  векторов,  вытекающие  из  его  определения:

1. 

(линейность  по  первому  аргументу),  здесь    —  вещественные  числа,  а    —  трехмерные  вектора;

2.    (симметричность);

3.  ,  причем    тогда  и  только  тогда,  когда  .

Используя  обозначения  скалярного  и  векторного  произведения  векторов,  покажем,  как  в  этих  обозначениях  выглядит  (выражается)  произведение  кватернионов.  Пусть    и    два  кватерниона,  где    и  -векторные  части  этих  кватернионов.  Тогда

.

Как  видим  эта  запись  произведения  гораздо  проще,  чем  соответствующая  запись  (11).  При  этом    -  скалярная  часть  кватерниона-произведения,  а    -  векторная  часть  кватерниона-произведения.

Вернемся  вновь  к  векторному  произведению  векторов.  Пусть  a,  b  и  c  –  трехмерные  вектора,  т.е.  ,  ,  .  Рассмотрим  векторное  произведение  :

.

Все  проделанные  выкладки  достаточно  очевидны,  кроме,  возможно,  добавления  в  соответствующем  равенстве  к  двум  соседним  слагаемым  с  противоположными  знаками  одного  и  того  же  слагаемого  с  противоположными  знаками.  Так  к  слагаемым    и    мы  добавили  слагаемое    и  слагаемое    и  т.  д.,  в  итоге  получили    и  т.  д. 

Пропуская  теперь  выкладки,  запишем  результат:

.

Используя  полученную  формулу,  теперь  легко  можно  доказать  тождество  Якоби

.

Действительно,

.

Заключение.  Отметим,  что  в  данной  статье  мы  ограничились  доказательством  алгебраических  свойств  кватернионов  и  лишь  частично  затронули  их  геометрические  свойства,  показав  как  из  кватернионов  появляется  векторное  и  скалярное  произведения  векторов.  В  следующей  статье  мы  покажем,  как  с  помощью  кватернионов  решается  такая  сложная  задача  как  «сложение  поворотов»  в  трехмерном  пространстве,  и  как  это  используется  в  механике  управляемого  движения.

Список  литературы:

1.            Бранец  В.Н.,  Шмыглевский  И.П.  Применение  кватернионов  в  задачах  ориентации  твердого  тела.  М.:  Наука,  1973.  —  320  с.

2.            Ишлинский  А.Ю.  Ориентация,  гироскопы  и  инерциальная  навигация.  М.:  Наука,  1976.  —  672  с.

3.            Кантор  И.Л.,  Солодовников  А.С.  Гиперкомплексные  числа.  М.:  Наука,  1973.  —  144  с.

4.            Кватернионы  в  геометрии,  механике,  релятивистской  физике,  теории  поля  //  fizteh.ru:  информационный  портал  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://www.fizteh.ru/02-07-90327/index/qwat/  (дата  обращения  25.01.2014).

5.            Побегайло  А.П.  Применение  кватернионов  в  компьютерной  графике.  Минск:  БГУ,  2010.  —  216  с.

6.            Хитров  Г.М.  Применение  второго  метода  Ляпунова  к  решению  задачи  ориентации  твердого  тела  //  Дифференциальные  и  интегральные  уравнения:  межвуз.  сб.,  Горький:  ГГУ,  1981.  —  С.  152—155.

7.            Цисарж  В.В.,  Марусик  Р.И.  Математические  методы  компьютерной  графики:  учебное  пособие.  К.:  Факт,  2004.  —  466  с.