ОБ  ОПТИМАЛЬНОМ  ЧИСЛЕ  РАВНОВЕРОЯТНЫХ  СТОЛБИКОВ  ГИСТОГРАММЫ

Бардасов  Сергей  Александрович

канд.  физ.-мат.  наук,  доцент  Тюменского  государственного  университета,  РФ,  г.  Тюмень

E-mail: 

ABOUT  OPTIMAL  NUMBER  OF  EQUIPROBABLE  HISTOGRAM  BARS

Sergey  Bardasov

candidate  of  Science,  assistant  professor  of  Tyumen  State  University,  Russia,  Tyumen

АННОТАЦИЯ

Рассматривается  вид  зависимости  оптимального  числа    равновероятных  столбиков  гистограммы  от  объема  выборки  .  Для  анализа  используется  информационный  критерий  Акаике.  Примеры  показывают,  что  при  большом  числе  наблюдений  число  интервалов    зависит  от    по  степенному  закону.  Однако  величина  показателя  степени  зависит  от  вида  функции  плотности  вероятностей.

ABSTRACT

The  type  of  dependence  of  optimum  number    of  equiprobable  histogram  bars  on  the  sample  size    is  considered.  For  the  analysisinformation  criterion  of  Akaike  is  used.  Examples  show  that  at  a  gross  sample  the  number  of  histogram  bins  depends  on    as  a  power  function.  However  the  size  of  an  exponent  depends  on  a  type  of  probability  density  function.

Ключевые  слова :  гистограмма;  информационный  критерий  Акаике

Keywords :  histogram;  Akaike  information  criterion

Если  длины  столбиков  гистограммы  равны,  то  упрощение  критерия  Акаике  при  большом  числе  наблюдений  приводит  к  критерию 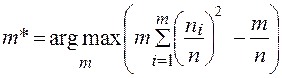 [1]: 

.  (1)

Полагая,  что    равно  вероятности  попадания  в  -ый  интервал  гистограммы  и  переходя  от  числа  интервалов    к  их  длине  ,  можно  показать,  что  оптимальное  значение    определяется  критерием

  .  (2)

Приравнивая  к  нулю  производную  по  ,  получим  известный  результат  Скотта  [2]: 

  (3)

Формула  (3)  первоначально  была  получена  методом  интегральной  среднеквадратической  ошибки.  Следовательно,  в  случае  равных  интервалов  длина  (число)  столбиков  гистограммы  обратно  пропорциональна  (пропорционально)  корню  третьей  степени  из  числа  наблюдений.  Представляет  интерес  рассмотреть  характер  подобной  зависимости,  когда  длины  интервалов  будут  различны.

Рассмотрим  случай  равновероятных  интервалов.  Такие  интервалы  часто  применяют  в  случае  сильно  неоднородных  распределений.  Информационный  критерий  Акаике  [3]  для  гистограммы  имеет  вид:

  .  (4)

где:    —  объем  выборки;

  —  число  столбиков  гистограммы;

  —  функция  правдоподобия  модели  (гистограммы). 

Множитель  2  в  формуле  (4)  имеет  историческое  происхождение,  в  дальнейшем  его  учитывать  не  будем.

Функция  правдоподобия  модели  имеет  вид:

где    —  длина  интервала  -го  столбика,  .

Логарифмируя  функцию  правдоподобия,  получим

Тогда  для  оценки  оптимального  числа  интервалов  гистограммы  получим:

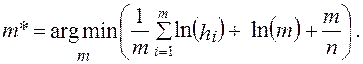  (5)

Как  показывают  нижеследующие  примеры  при  больших  объемах  выборки  вид  асимптотической  зависимости  числа  столбиков    гистограммы  с  равновероятными  интервалами  неодинаков  для  различных  распределений.

Пусть  плотность  распределения  имеет  вид:

  (6)

Разделим  отрезок    на    частей,  имеющих  длины  ,  которые  при  большом  объеме  выборки  можно  оценить  из  условия: 

  (7)

Согласно  (7)  получим 

Следовательно,  оптимальное  число  групп  ,  находится  из  условия:

Оценим  выражение

.

Заметим,  что 

  .

Оценим  сумму    по  формуле  Эйлера-Маклорена:

  .

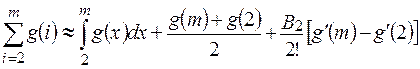Вычисляя,  получим:

.

После  упрощений  и  разложения  в  ряд  по  степеням  ,  с  точностью  до  величин  порядка  ,  имеем:

Приравняем  производную  к  нулю,  тогда  оптимальное  число  интервалов  будет  равно

,

.  (8)

Пусть  плотность  распределения  имеет  вид:

  (9)

В  этом  случае  длины  интервалов  определяются  из  условия:

Тогда 

Следовательно,  оптимальное  число  групп  ,  находится  из  условия:

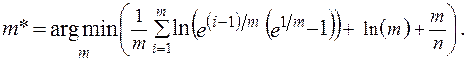
Проведем  вычисления

Разлагая  показательную  и  степенную  функции  по  степеням  ,  получим:

.

Приравняем  производную  последнего  выражения  к  нулю,  получим:

.

Тогда  число  интервалов  гистограммы  для  функции  плотности  (5)  при  большом  числе  наблюдений  равно:

.  (10)

Таким  образом,  в  рассмотренных  примерах  согласно  критерию  Акаике  в  случае  равновероятных  интервалов  зависимость  числа  интервалов  гистограммы  от  объема  выборки  при  большом  числе  наблюдений  приближенно  подчиняется  степенной  зависимости.  Однако  величина  показателя  степени  зависит  от  вида  функции  плотности  распределения  вероятностей. 

Список  литературы:

1.Бардасов  С.А.  Упрощение  критерия  Акаике  для  гистограммы.  В  сб.:  «Физико-математические  науки  и  информационные  технологии:  теория  и  практика»:  материалы  международной  заочной  научно-практической  конференции.  Новосибирск:  Изд.  «СибАК»,  2012.  —  C.  8—13.

2.Scott  D.W.  On  optimal  and  data-based  histograms  //  Biometrika.  —  1979.  —  Vol.  66.  —  P.  605—610.

3.Akaike  H.  Information  theory  as  an  extension  of  the  maximum  likelihood  principle.  In  B.  N.  Petrov  &  F.  Csaki  (Eds.).  Second  International  Symposium  on  Information  Theory.  Budapest:  Akademiai  Kiado,  1973.  —  P.  267—281.