ЛОКАЛЬНАЯ ТЕХНОЛОГИЯ ИСПОЛЬЗОВАНИЯ ГРАФИЧЕСКОГО МОДЕЛИРОВАНИЯ ПРИ РЕШЕНИИ ТЕКСТОВЫХ ЗАДАЧ, ДЛЯ РАЗВИТИЯ ЛОГИЧЕСКОГО МЫШЛЕНИЯ МЛАДШИХ ШКОЛЬНИКОВ

Ягодина Елизавета Викторовна

 учитель начальных классов МОУ «Крест – Хальджайская средней общеобразовательной школы им. Героя Советского Союза Ф.М.Охлопкова»

с. Крест-Хальджай, Томпонский район, Республика Саха (Якутия)

E-mail: eliza-yagotka@mail.ru

Умение решать текстовые задачи является одним из основных показателей уровня математического развития ребенка, глубины усвоения им учебного материала.

Как известно, работа над задачей начинается со знакомства с ее текстом. Уже при этом первичном знакомстве происходит анализ, цель которого выделение «ведущего» отношения среди множества других, установление связей между тем, что дано, и тем, что требуется найти. На первый взгляд в этом нет ничего сложного, но действительность убеждает в обратном: нередко у учащихся формируется привычка выделения, выхватывания отдельного слова из контекста задачи как опорного, без осознания конкретного содержания, что и приводит к ошибочным решениям. Для устранения этого используются различные методические приемы, способствующие осмыслению текста задачи: представление жизненной ситуации, которая описана в задаче, мысленное участие в ней, разбиение текста задачи на смысловые части, отбрасывание несущественных слов в условии задачи но, чтобы каждый ученик мог выделить все отношения при первичном анализе задачи, их нужно увидеть [2, c. 78].

Поэтому одним из основных приемов в анализе задачи является графическое моделирование, которое помогает ученику не только понять задачу, но самому найти рациональный способ ее решения.

Использование графическое моделирование позволяет построить процесс знакомства с задачей на основе частично-поискового метода: при таком подходе после решения простой задачи достаточно задать еще один вопрос, и схема приобретает новый вид, моделируя ситуации текстовой задачи [7 c. 56].

Мы попытаемся подробно изложить технологию использования графического моделирования как педагогического инструмента развития логического мышления при ознакомлении с решением задач.

Технология 1.Обучение детей преобразованию предметных действий в работающую модель.

Задачи на нахождение суммы и остатка являются первыми задачами, с которыми встречаются дети, и важно, чтобы каждый ребенок понял, каким действием решается задача и почему.

Задача 1.Уйгулаана вымыла 3 большие чашки и несколько маленьких. Всего она вымыла 5 чашек. Сколько маленьких чашек вымыла Уйгулаана?

Отв: Уйгулаана вымыла 2 маленькие чашки.

Задача 2.Когда с полки сняли 2 книги, там осталось 4. Сколько книг лежало на полке сначала?

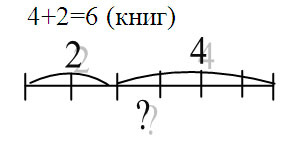
Отв: На полке было 6 книг.

Задача 3.В вазе лежало 7 помидоров, за обедом съели 3 помидора. Сколько помидоров осталось в вазе?

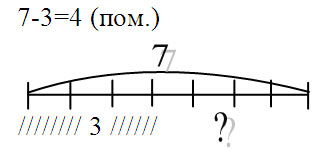
Отв: В вазе осталось 4 помидора.

Технология 2.Обучение детей составлению обратных задач к данной основе работы с графической моделью.

При обучении детей составлению обратных задач к данной основе с моделью желательно ознакомить их сразу с группой задач, которые разбиваются на 3 блока:

1.    блок. Основная задача — на конкретный смысл действия сложения; обратные — на нахождение неизвестного слагаемого.

2.    блок. Основная задача — на конкретный смысл вычитания; обратные — на нахождение неизвестного уменьшаемого или вычитаемого.

3.    блок. Основная задача — на увеличение числа на несколько единиц в прямой форме; обратные — на уменьшение числа на несколько единиц в косвенной форме и на разностное сравнение [5, c. 109]

Рассмотрим работу над основной задаче первого блока.

Задача 4.Сардаана нарисовала 5 красных яблок и 3 зеленых яблока. Сколько яблок нарисовала Сардаана?

На конкретный смысл действия сложения

а) 5+3=8 (ябл.)

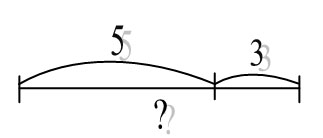
Отв: Сардаана нарисовала 8 яблок.

На нахождение неизвестного слагаемого

б) 8-3=5 (красн. ябл.)

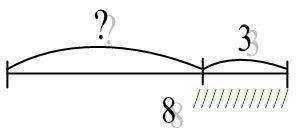
Отв: Сардаана нарисовала 5 красных яблок.

Рассмотрим пример основной задачи второго блока.

Задача 5.В кытыйе лежало 7 лепешок, за обедом съели 3 лепешки. Сколько осталось лепешек в кытыйе?

На конкретный смыл вычитания

а) 7-3=4 (леп.)

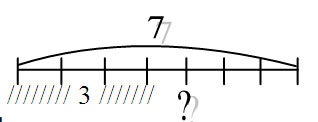
Отв: В кытыйе осталось 4 лепешки.

На нахождение неизвестного уменьшаемого или вычитаемого

б) 7-4=3 (леп.)

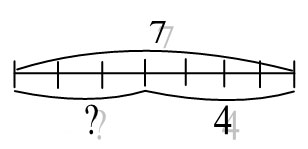
Отв: За обедом съели 3 лепешки.

Рассмотрим пример основной задачи третьего блока.

Задача 6.Дайаана посадила 3 куста смородины, а Дьулус на 2 куста больше, чем Дайаана. Сколько кустов смородины посадил Дьулус?

а) На увеличение числа на несколько единиц.

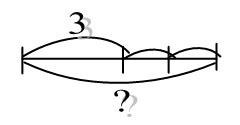
3+2=5 (куст. см.)

Отв: Дьулус посадил 5 кустов смородины.

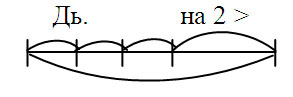
Дь                на 2 >

б) На уменьшение числа на несколько единиц в косвенной форме и на разностное сравнение.

Отв: Дьулус посадил больше Дайааны на 2 куста смородины.

Технология 3.Задачи, раскрывающие на конкретный смысл действий умножения и деления.

При ознакомлении с решением задач на нахождение произведения учащиеся усваивают то, что если мы при решении задачи получаем сумму одинаковых слагаемых, то задачу можно решить умножением. И здесь моделирование поможет им понять выбор действия. Например, предлагается задача:

Задача 7.4 ученика сделали по 2 кубика каждый. Сколько кубиков сделали ученики?

Задача иллюстрируется предметным моделированием: вызван­ный ученик берет по 2 кубика 4 раза и складывает в коробку, сопровождая свои действия словами: «Эти кубики сделал первый ученик, эти кубики сделал второй ученик…»

Учитель с классом проводит беседу, задавая следующие вопросы — обсуждения:

У. По сколько кубиков он брал за один раз?

Д. По два.

У. Сколько раз он брал по два кубика?

Д. Четыре раза.

У. Как мы изобразим кубики в тетради?

Д. Квадратами.

У. Нарисуйте два квадрата и обведите их. Эти кубики он взял первым. Он брал еще три раза по столько же. Мы не будем рисовать еще три раза все квадраты, а покажем овалом, что он брал по столько же, а сверху напишем, что он брал четыре раза. Внизу изобразим скобку и вопросительный знак, так как в задаче спрашивается, сколько кубиков сделали ребята [6, c. 217].

В результате в тетрадях получается модель задачи в виде схематического рисунка.

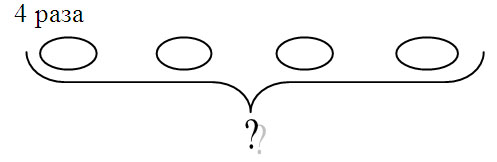
На вопрос учителя: «Как можно решить эту задачу?», дети рассуждают: «Чтобы узнать, сколько кубиков надо прибавит два, еще прибавит два и еще прибавит два, получиться восемь. Но здесь четыре одинаковых слагаемых, значит, задачу можно решить умножением: по два взять, четыре раза, или два умножит на четыре, получиться восемь».

Решение задач на первых порах записываем сложением и умножением, чтобы учащиеся лучше усвоили смысл каждого компонента. Переходим к записи решения только умножением тогда, когда сами дети предлагают ее минуя запись в идее суммы [4, c. 94].

С целью предупреждения ошибок на перестановку множителей в записи решения задачи, можно предложить задания: составить модель задачи к выражению 3х4.

Выбери схему к задаче и реши ее:

В 4 кучках по 3 морковки. Сколько всего морковок?

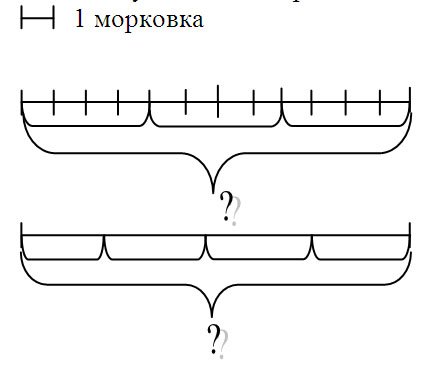
Подготовительная работа к решению задач на деление по содержанию начинается в 1 классе. На этом этапе можно применить практикой выполнение упражнений вида:

а.    Возьмите 8 кружков и разложите их по 2 сколько раз по 2 кружка получилось?

б.    12 карандашей разложили в коробки по 6 карандашей в каждую. Сколько потребовалось коробок?

Учащиеся выполняют соответствующие операции и находят результат: сосчитай, сколько раз по 2 кружка получилось или сколько потребовалось коробок. При этом следует обратить внимание детей, что карандашей в коробках получается поровну.

Последним процесс построения схематических рисунков на примерах задач:

Задача8. 12морковок связали в пучки, по 4 морковки в каждом. Сколько пучков получилось?

У. Сколько всего морковок нужно связать в пучки?

Д. Двенадцать.

У. Нарисуем их в виде квадратиков.

Дети выполняют рисунок

У. По сколько морковок брали в один пучок?

Д. По четыре.

У. Давайте отделим четыре морковки и т.д.

Дети выполняют рисунок.

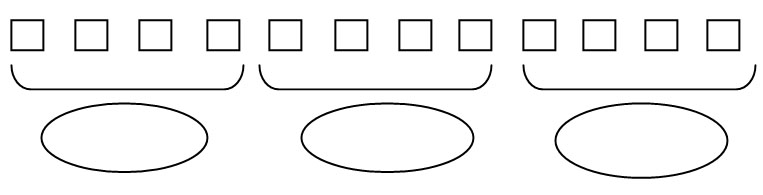
Такая модель дает возможность детям уяснить путем конкретного действия смысл деления по содержанию, когда заранее неизвестно число частей (кучек, пучков, и т.д.), которые должны получиться в результате деления.

Отделяя по 4 морковки в каждый пучок, дети убеждаются, что получаются три таких пучка, и записывают решение: 12:4=3 (п.) и ответ (3 пучка).

Приведенный выше материал показывает, что рисунки и чертежи используются не только иллюстрации условия задачи, но и как средство их графического решения.

Необходимость в таком использовании рисунков и чертежей отпадает тогда, когда дети могут решать задачи по представлению. В дальнейшем графический способ решения таких задач может выступать как средство проверки правильности решения задачи арифметическом способом [5, c. 119].

В начальном курсе математики под понятием «задача» понимается текстовая задача, которая формируется в идее текста, в котором находят количественные отношения между реальными объектами. Эти задачи являются тем конкретным материалом, с помощью которого формируются у детей новые знания и закрепляются в процессе уже имеющиеся знания.

Научить детей решать задачи — значит, научить их устанавливать связи между данными и искомыми, и в соответствии с этим выбирать, а затем и выполнять арифметические действия [7, c. 105].

Процесс графического моделирования задачи повышает мыслительную активность детей, способствует вариативность логического мышления, значит, делает решение задач более приятным и интересным.

Список литературы:

1.Александрова Э. И. Математика: учеб. пособие. М.: Дом педагогики, 2000.

2.Выготский Л. С. Педагогическая психология. М: Педагогика, 1991.

3.Гальперин П. Я. Учебная деятельность и моделирование. М.: Просвещение, 1995.

4.Давыдов В. В. Учебная деятельность и моделирование. Ереван, 1982.

5.Зайцева С. А. Моделирование текстовых задач // Начальная школа 2005. № 4.

6.Сигал Л. М. Развитие логического мышления учащихся в процессе выполнения ими учебно-логических заданий. М.: Просвещение, 1979.

7.Тихомирова А. Ф., Басов А. В. Развитие логического мышления детей. Яр., 1997.