Статья опубликована в рамках: V Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 14 ноября 2011 г.)
Наука: Технические науки
Секция: Энергетика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
МОДЕЛИРОВАНИЕ ГИДРОДИНАМИЧЕСКИХ ПРОЦЕССОВ В СУПЕРКАВИТАЦИОННОМ ИСПАРИТЕЛЕ
Кулагин Владимир Алексеевич
д. т. н., профессор СФУ, г. Красноярск
Е-mail: v.a.kulagin@mail.ru
Пьяных Татьяна Анатольевна
аспирант СФУ, г. Красноярск
Е-mail: T.Pyanykh@gmail.com
Вопросы рационального использования водных ресурсов приобретают сегодня особо важное значение в мировом масштабе. В настоящее время все больше стран начинают принимать срочные меры по предотвращению водного кризиса. Современное производство тепловой и электрической энергии сопровождается использованием значительного количества пресной воды и сбросом в окружающую среду больших объемов сточных вод разного уровня загрязненности. Проблема дефицита пресной воды наряду с такими вопросами, как очистка сточных вод и борьба с загрязнениями водоемов, может быть решена путем максимально возможного использования в промышленности минерализованных вод и их опреснения.
В настоящее время известны более двадцати методов опреснения соленых и солоноватых вод. Некоторые из методов доведены до промышленной реализации в крупных масштабах, другие находятся в стадии поисковых исследований. Заметные экологические преимущества, свойственные термическому методу водоподготовки, а также возможность переработки с его помощью промышленных минерализованных сточных вод, объясняют широкое распространение этого метода.
Однако несовершенство процессов теплообмена и испарения, накипеобразование, большие габариты, невысокая энергонапряженность теплообменной поверхности и ряд других недостатков требуют не только усовершенствования существующих термических установок для обессоливания, но и создания новых аппаратов с более высокими технико-экономическими характеристиками.
Использование режимов развитой кавитации позволяет исключить существенные недостатки термического метода опреснения. Кавитационный метод интенсификации теплообмена заключается в том, что при обтекании недогретой жидкостью кавитатора в рабочем модуле суперкавитационных испарительных камер образуются суперкаверны, из которых производится пароотбор [1]. На рисунке 1 представлена схема суперкавитационного испарения.
Рисунок 1. Физико-механическая модель суперкавитационного испарения

1 – кавитатор, 2 – труба круглого сечения, 3 – суперкаверна, 4 – отбор пара из каверны
Эффективность суперкавитационных испарителей главным образом определяется величиной поверхности испарения, которая в свою очередь зависит от многих факторов, определяющими из них являются величина отбора пара, число кавитации, число Фруда, степень стеснения потока, величина недогрева рабочей жидкости, физические свойства жидкости.
Одновременное существование граничной динамики, фазового перехода и сильного изменения плотности значительно затрудняет задачу исследования рабочих процессов суперкавитационных испарителей.
В данной работе для оценки поверхности кавитационного испарения используется модель двухфазного гомогенного потока, в которой поток рассматривается как гомогенная смесь. Эта модель основывается на предположении локального кинематического и термодинамического равновесия между фазами и не предполагает поверхность раздела между двумя несмешивающимися жидкостями. Объемная доля фазы может изменяться от нуля до единицы, в зависимости от занимаемого пространства в двухфазном потоке. Задача рассматривается в стационарной постановке и предполагает решение следующих уравнений (1)-(6):
уравнения неразрывности для каждой фазы ![]()
|
|
(1) |
где ![]() – объемная доля фазы
– объемная доля фазы ![]() ;
; ![]() – плотность фазы
– плотность фазы ![]() , кг/м3;
, кг/м3; ![]() – массовая скорость образования фазы, кг/м3с;
– массовая скорость образования фазы, кг/м3с; ![]() – скорость смеси, м/с;
– скорость смеси, м/с;
уравнение движения для смеси
|
|
(2) |
где ![]() – плотность смеси, кг/м3;
– плотность смеси, кг/м3; ![]() – коэффициент кинематической вязкости смеси, Па·с;
– коэффициент кинематической вязкости смеси, Па·с; ![]() – давление, Па.
– давление, Па.
Турбулентность учитывается использованием ![]() модели. Уравнения переноса для кинетической энергии турбулентности
модели. Уравнения переноса для кинетической энергии турбулентности ![]() , м2/с2, и ее диссипации
, м2/с2, и ее диссипации ![]() , м2/с3:
, м2/с3:
|
(3) |
|
(4) |
где ![]() – скорость генерации турбулентности,
– скорость генерации турбулентности, ![]() – турбулентная вязкость. Эмпирические константы имеют следующие значения:
– турбулентная вязкость. Эмпирические константы имеют следующие значения: ![]() =1;
=1; ![]() =1,3;
=1,3; ![]() =1,44;
=1,44; ![]() =1.92.
=1.92.
Так как фазы должны полностью заполнять весь объем, то принимается следующее условие:
|
|
(5) |
Для массовой скорости образования фазы используется кавитационная модель [2]:
|
|
(6) |
где ![]() – объемная доля зародышей («ядер») кавитаций,
– объемная доля зародышей («ядер») кавитаций, ![]() – радиус зародыша кавитации, м. При моделировании применялись следующие параметры модели:
– радиус зародыша кавитации, м. При моделировании применялись следующие параметры модели: ![]() = 10−6 м,
= 10−6 м, ![]() = 5·10−4,
= 5·10−4, ![]() =50 и
=50 и ![]() = 0,01.
= 0,01.
Для апробации модели были проведены расчеты на холодной воде (20 °С), так как такие режимы можно считать предельными по температуре ведения процесса для кавитационного испарения. В качестве кавитатора использовался конус с диаметром основания 16 мм, и углом раствора конуса 53°. Степень стеснения потока принималась равной 0,29. Численный эксперимент проводился при постоянном значении числа Фруда 37,4.
На рисунке 2, в качестве примера, представлена доля пара в смеси при различных числах кавитации.
Рисунок 2. Расчетные результаты распределения доли пара при разных числах кавитации: а – число кавитации 0,46; б – число кавитации 0,465; в – число кавитации 0,47
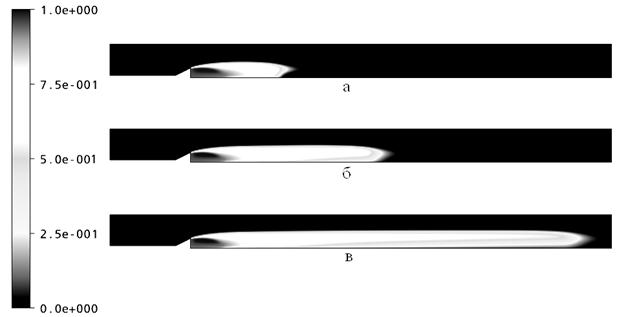
Рисунок 3. Зависимость относительной длины каверны от числа кавитации

На рисунке 3 отображена зависимость относительной длины каверны от числа кавитации.
Анализ полученных результатов показывает, что при постоянных значениях коэффициента стеснения потока и числа Фруда увеличение числа кавитации приводит к росту размеров каверны.
Суперкавитационный метод является перспективным способом опреснения и требует дальнейшего изучения. Результаты проведенных исследований показывают, что представленную модель можно использовать для анализа и совершенствования рабочих процессов в суперкавитационных испарителях.
Список литературы:
1. Ивченко В.М., Кулагин В.А., Немчин А.Ф. Кавитационная технология: монография. Красноярск: Изд-во КГУ, 1990. – 200 с.
2. Philip J.Z. A Two-Phase Flow Model for Predicting Cavitation Dynamics / Philip J. Zwart, Andrew G. Gerber, Thabet Belamri // International Conference on Multiphase Flow. 2004. №152. ‑ p. 45–56.
дипломов






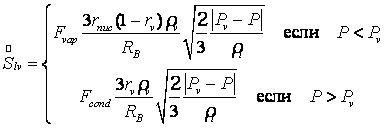
Комментарии (1)
Оставить комментарий