ПРИМЕНЕНИЕ НЕЧЕТКОЙ КЛАСТЕРИЗАЦИИ ДЛЯ АВТОМАТИЗАЦИИ ПОИСКА ПОХОЖИХ ПОКУМЕНТОВ

Аликов Алан Юрьевич

канд. техн. наук, доцент СКГМИ, г. Владикавказ

E-mail:

Калиниченко Алла Викторовна

ассистент, СКГМИ, г. Владикавказ

E-mail: kalinichenkoalla@mail.ru

1.     Введение

Поиск похожих документов нацелен на нахождение документов, тематически близких документу-образцу. В этом виде поиска документ-образец выступает в качестве запроса. В данной статье рассматривается возможность применения нечеткой кластеризации к решению задачи поиска похожих документов.

2. Нечеткая кластеризация

Целью кластеризации коллекции документов является автоматическое выявление групп семантически похожих документов. Особенность нечеткой кластеризации состоит в том, что кластеры являются нечеткими множествами и каждый элемент принадлежит различным кластерам с различной степенью принадлежности. Рассмотрим алгоритм нечеткой кластеризации fuzzy C-Means и кластеризацию по Гюстафсону-Кесселю.

Пусть множество исходных данных , . Вектор центров кластеров . Матрица разбиения . Целевая функция , где  - показатель нечеткости. Набор ограничений: , , ,  который определяет, что каждый вектор данных может принадлежать различным кластерам с разной степенью принадлежности, сумма принадлежностей элемента данных всем кластерам пространства разбиения равна единице.

Алгоритм fuzzy C-Means. Основные шаги:

Шаг 1. Выбрать количество кластеров .

Шаг 2. Выбрать скалярную метрику для отображения векторов данных на вещественную ось.

Шаг 3. Выбрать параметр остановки δ.

Шаг 4. Выбрать коэффициент нечеткости .

Шаг 5. Проинициализировать матрицу разбиения.

Шаг 6. Вычислить центры кластеров по формуле: .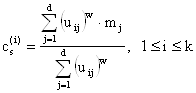

Шаг 7. Для всех элементов данных вычислить квадраты расстояний до всех центров кластеров по формуле: .

Шаг 8. Обновить матрицу  для всех , учитывая набор ограничений.

Шаг 9. Проверить условие: . Если условие выполняется, то завершить процесс, если нет – перейти к шагу 6 с номером итерации .

Алгоритм кластеризации по Гюстафсону-Кесселю.

Кластер характеризуется не только своим центром, но и ковариационной матрицей. Основные шаги алгоритма:

Шаг 1. Выбрать количество кластеров .

Шаг 2. Выбрать параметр остановки δ.

Шаг 3. Выбрать коэффициент нечеткости .

Шаг 4. Проинициализировать матрицу разбиения.

Шаг 5. Рассчитать центры кластеров по формуле: .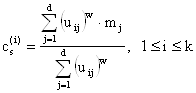

Шаг 6. Рассчитать ковариационные матрицы кластеров по формуле: .

Шаг 7. Вычислить расстояния по формуле:

.

Шаг 8. Обновить матрицу  для всех , учитывая набор ограничений.

Шаг 9. Проверить условие: . Если условие выполняется, то завершить процесс, если нет – перейти к шагу 5 с номером итерации .

Алгоритм fuzzy C-Means формирует кластеры сферической формы, что подходит далеко не для всех задач. Алгоритм кластеризации по Гюстафсону-Кесселю находит кластеры в форме эллипсоидов, что делает его более гибким при решении задач. Существует ряд алгоритмов, подобных описанным, единственное отличие которых состоит в дополнительных слагаемых целевой функции, которые учитывают некоторые другие аспекты взаимосвязи данных [1].

3. Поиск похожих документов

Модифицированной формой представления информационных интересов пользователя является поиск похожих документов (similar document search). Целью поиска является обнаружение документов, тематически близких документу-образцу. Под тематической близостью понимается близость по содержанию, смыслу [2].

 – конечное множество документов в текстовой коллекции;

 – общее количество документов;

 – множество терминов в коллекции документов;

 – общее количество терминов;

Как правило, документ в поисковой системе описывается набором ключевых слов, что, естественно, не позволяет в полной мере отразить его смысл [3]. Рассмотрим поисковый образ документа, учитывающий контекст терминов. Представим документ  в виде набора: , где

 - нечеткое множество,  - степень принадлежности термина  документу ;

 – нечеткое множество, описывающее ассоциативную связь терминов документа. , зависит от частоты совместной встречаемости терминов в одном контексте.

Пусть , ,  - поисковые образы  и  соответственно. Поскольку поисковый образ представляет собой пару нечетких множеств, то при вычислении меры близости документов следует отдельно вычислить меру близости множеств  и .

Основные этапы предлагаемого подхода к поиску похожих документов представлены на рис 1. В блоке 1 производится предварительная обработка документов, включающая в себя лексический анализ, морфологический анализ, удаление стоп-слов, приведение регистра. Формирование поискового образа документов и расширенного поискового образа документа-образца происходит в блоках 2 и 3 соответственно. В блоке 4 осуществляется кластеризация документов коллекции, в результате которой будут вычислены центры кластеров  и сформирована матрица разбиения , где  - степень принадлежности документа  кластеру . В блоке 5 определяются наиболее близкие кластеры для заданного пользователем документа-образца. Документы этих кластеров образуют множество «документов-кандидатов». Вычисление степени сходства расширенных поисковых образов «документов-кандидатов» и расширенного поискового образа документа-образца происходит в блоке 6.

Рисунок 1. Основные этапы алгоритма поиска похожих документов.

4. Заключение

В работе рассмотрена возможность применения кластеризации при поиске похожих документов. Кластеризация документов позволяет существенно снизить размерность данных, проверяемых на сходство с документом-образцом.

Список литературы:

1.            Барсегян А. А., Куприянов М. С., Степаненко И. И., Холод И. И. Технологии анализа данных: Data Mining, Visual Mining, Text Mining, OLAP. – СПб.: БХВ-Петербург, 2007. 384 с.

2.            Калиниченко А. В. О методах поиска по документу-образцу в коллекции электронных документов // X Международная научно-практическая конференция «ИТ-технологии: Развитие и приложения»: материалы. Владикавказ. 2009. С. 50–59.

3.            Dominich S. The Modern Algebra of  Information Retrieval. Springer Verlag, 2008. 327 p.