Статья опубликована в рамках: VI Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 16 января 2012 г.)
Наука: Технические науки
Секция: Энергетика
Скачать книгу(-и): Сборник статей конференции, Сборник статей конференции часть II
- Условия публикаций
- Все статьи конференции
дипломов
ВЫЧИСЛЕНИЕ УСТАНОВИВШЕГОСЯ РЕЖИМА СЕТИ ПЕРЕМЕННОГО ТОКА СО ВСТРОЕННОЙ ЛИНИЕЙ ПОСТОЯННОГО ТОКА
Крживка Владимир
Докторант, Чешский технический университет, г. Прага
В качестве способа расчета установившегося режима предлагается метод Ньютона, рассмотрен алгоритм метода, предоставлены расчеты как конфигурации с передачей энергии только с помощью переменного тока, так и конфигурации со встроенной веткой передачи энергии с помощью постоянного тока.
Установившийся режим – рабочее состояние сети, т. е. состояние при котором не происходит переход от одного режима в другой, например, не происходит измена конфигурации сети (включение, отключение электрических линий) Для того, чтобы вычислить установившийся режим сети данной конфигурации, надо знать постоянные и переменные параметры отдельных линий (мощности, подаваемые генераторами на сеть, расход мощности, напряжнения в узлах и т. п.). Поставленной задачей является расчет недостающих параметров для нахождения значения установившегося режима.
Во-первых, определим известные параметры в узлах и какие необходимо рассчитать. Для точного описания каждого узла имеются четыре параметра:
Активная (полезная) мощность P (МВт) – входная или выходная;
Реактивная мощность Q (МВАр) - входная или выходная;
Амплитуда напряжнения U (кВ);
Фазовый угол напряжнения δ (градусы).
Разделим все узлы по пинципу известных и неизвестных параметров (см. Таблицу 1).
Таблица 1- Разделение узлов сети
Вид узла |
Реализация узла |
U |
δ |
P |
Q |
Slack (Uδ) |
Балансный узел (обычно один), большой источник электроэнергии (электростанция), эквивалент подключеной системы (сети), фаза δ и фазы остальных узлов суммируются с учетом знака, по значению мощностей разделяют на избыточную и недостаточно |
знаем |
0 |
? |
? |
PU |
Генераторные узли с функцией регуляции напряжнения |
знаем |
? |
знаем |
? |
PQ |
Балластные узлы (точки расхода) |
? |
? |
знаем |
знаем |
Различают постоянные и переменные параметры.
Постоянные параметры – параметры, которые в ходе нахождения значения установившегося режима не изменяются, для узлов вида PQ и PU это величины активных мощностей, из которых состоит вектор столбцов PPQPU и для узлов вида PQ величины реактивных мощностей, из которых составим вектор столбцов QPQ. Вместе эти векторы-столбцы создают один вектор-столбец константных параметров сети, который обозначим символом Γ:
 .
.
Параметры состояниий – это все неизвестные величины, которые необходимо найти. Эти случайные параметры изменяются во время расчета так, чтобы был достигнут исходный баланс мощностей в сети. Вектор сосояний величин![]() состоит из вектора-столбца напряженией
состоит из вектора-столбца напряженией ![]() в узлах PQ и из вектора-столбца фаз напряженией
в узлах PQ и из вектора-столбца фаз напряженией ![]() в узлах PQ и PU:
в узлах PQ и PU:
 .
.
Для токов в узлах обыкновенной электрической сети (n узловых точек) справедливо:
![]() ,
,
где ![]() - матрица узловых напряженией;
- матрица узловых напряженией;
![]() - адмитантная матрица (комплексная, симметричная, квадратная, разряженная) системы с известными параметрами линией, определяется как:
- адмитантная матрица (комплексная, симметричная, квадратная, разряженная) системы с известными параметрами линией, определяется как:
 ,
,
где ![]() - продольный адмитанц, плечо между узлами i и k,
- продольный адмитанц, плечо между узлами i и k,
![]() - диагональный адмитанц, сложение всех адмитанций плеч прицепных в узел i.
- диагональный адмитанц, сложение всех адмитанций плеч прицепных в узел i.
Расходы мощностей в отдельных узлях i определим:
![]() ,
,
где ![]() - предполагаемая мощность (ВА),
- предполагаемая мощность (ВА), ![]() - комплексный ток (A), i – i-тый узел.
- комплексный ток (A), i – i-тый узел.
Вместо тока в (1.5) подставим требуемый узловой ток из (1.3) и получим:
 .
.
Если расписать напряжение в экспоненциальной форме с использованием адмитанции, получим:
![]()
Применим Эйлерову формулу (1.8) для комплексных чисел к (1.7), получим (1.9):
![]() .
.
![]() ,
,
где G – потери (Сиеменс), B – реактивная проводимость (Сиеменс).
После разложения предполагаемой мощности из (1.9) на реальную и мнимую (имагинарную) части получим формулы для активной (1.10) и реактивной мощностей (1.11) для i-того узла:
![]() ,
,
![]()
Уравнения (1.10 и 1.11) описывают i-тый узел вида Slack. Пользуясь Таблицей 1 из этих уравнений выразим требуемые величины а для i-тых узлов вида PQ и PU,таким образом получим нелинерную систему уравнений (потери мощностей зависят от квадрата тока).
Определим выражение электропередачи постоянного тока в сети. Передачу постоянного тока HVDC представим в виде двух узлов:PU в начале передачи и PQ в конце. Для схемы HVDC обратной связью учитываем потери передачи, тогда расходная мощность в узле PU будет равна поставляемой мощности в узле PQ. В случае биполярной или монополярной схемы HVDC передачи должны учитываться потери в линиях сети. Из выражения известной величины мощности PU в начале линии найдем ток и потери для PQ узла. Под входной мощностью будем понимать такую мощность, которая равна мощности в узле PU с учетом потерь (см. Рис. 1).
Рисунок 1. HVDC в сети

Разницу между мощностями в начале и конце линии вычислим по формуле:
 . (1.12)
. (1.12)
Для нахождения установившегося режима сети необходимо найти определенные выше параметры, так как при решении системы уравнений традиционные алгебраические методы дают ответ с погрешностью из-за нелинейности уравнений, для решения был выбран один из наиболее часто используемых итерационных методов: метод Ньютона (Ньютн-Рапшонов метод) или метод касательных в зависимости от искомых величин и точности.
Для поиска решения векторной функции ![]() векторного аргумента
векторного аргумента ![]() используется Ньютн-Рапшнов метод, процесс аналогичен как поиску решения для скалярной функции с одним переменным значенем. Общая формула для нахождения значений:
используется Ньютн-Рапшнов метод, процесс аналогичен как поиску решения для скалярной функции с одним переменным значенем. Общая формула для нахождения значений:
![]() , (1.13)
, (1.13)
где ![]() - матрица Якоби, которая определяется следующим образом:
- матрица Якоби, которая определяется следующим образом:
 . (1.14)
. (1.14)
Матрица ![]() для функции
для функции ![]() имеет смысл производной в одномерных моделях (касательной в точке, относительно которой проводим линеаризацию). Зависимость между приростом вектора независимых значений и дефектом выражается следующей формулой:
имеет смысл производной в одномерных моделях (касательной в точке, относительно которой проводим линеаризацию). Зависимость между приростом вектора независимых значений и дефектом выражается следующей формулой:
![]() . (1.15)
. (1.15)
Искомое значение ![]() является вектором (постоянных) величин
является вектором (постоянных) величин![]() и зависимого значения
и зависимого значения ![]() . Соотношения между узловыми параметрами при сохранении фиксированных параметров
. Соотношения между узловыми параметрами при сохранении фиксированных параметров ![]() в конце расчета задает система уравнений (1.10 и 1.11).
в конце расчета задает система уравнений (1.10 и 1.11).
Рисунок 2. Алгоритм решения установившегоя режима сети

Опишем алгоритм нахождения установившегося режима в сети (Рис. 2).
Во-первых, введем начальные данные (известные) величины ![]() , которые задают ограничения. Дальше выбираем инициализации начальных значенией s постоянных величин
, которые задают ограничения. Дальше выбираем инициализации начальных значенией s постоянных величин ![]() ,т. е.
,т. е. ![]() . Затем подставим в систему уравненей и определим зависимые переменные величины, т. е.
. Затем подставим в систему уравненей и определим зависимые переменные величины, т. е. ![]() , и установим (дефект)
, и установим (дефект) ![]() зависимых переменных величин от неизвестных значенией, которые необходимо расчетать. Если дефект больше чем вабранная граница
зависимых переменных величин от неизвестных значенией, которые необходимо расчетать. Если дефект больше чем вабранная граница  , составим матрицу Якоби линеаризующую функциональные формулы в окружности нужной точки. Матрица Якоби состоит из частных производных зависимых переменных величин, соответственно со всеми независимыми переменными, которые определены в каждом узле. Количество рядов и столбцов матрицы равно числу количества узлов PQ умноженного на два с добавлением количества узлов PU. Матрицу Якоби представляет соотношение (1.16).
, составим матрицу Якоби линеаризующую функциональные формулы в окружности нужной точки. Матрица Якоби состоит из частных производных зависимых переменных величин, соответственно со всеми независимыми переменными, которые определены в каждом узле. Количество рядов и столбцов матрицы равно числу количества узлов PQ умноженного на два с добавлением количества узлов PU. Матрицу Якоби представляет соотношение (1.16).
 . (1.16)
. (1.16)
Отдельные элементы матрицы (i,k) можно определить обычными дифференциальными уравнениями (1.10 и 1.11):
![]() , (1.17)
, (1.17)
![]() , (1.18)
, (1.18)
![]() , (1.19)
, (1.19)
![]() (1.20)
(1.20)
![]() , (1.21)
, (1.21)
![]() , (1.22)
, (1.22)
![]() , (1.23)
, (1.23)
![]() (1.24)
(1.24)
Получим сложную матрицу Якоби, которая отражает соотношение между приростом независимо переменных величин и дефектом. Необходимо провести инверсию матрицы Якоби, после этого вычислим коррекцию  (аналогично с (1.20)):
(аналогично с (1.20)):
![]() . (1.25)
. (1.25)
Установим новые данные независимо переменных величин  :
:
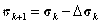 . (1.26)
. (1.26)
Этим приблизимся к искоемуму решению. После приведения в порядок конкретные ограничивающие условия, повторяем расчет функционных значениий по алгоритму с расчетом дефекта до тех пор, пока дефект не станет меньше чем заданное ограничение.
Продемонстрируем данный способ на примере (см. Рис. 3).
Рисунок 3. Экспериментальные конфигурации сети: а) с передачей только с помощью переменного тока, б) с передачей с помощью переменного тока с линией (между 5 и 8 узлами) передачи постоянным током .

Параметры узлов заданы в таблице 2 (см. Таблица 2).
Таблица 2. Начальные значения узловых данных в сети с передачей по переменному току
Номер узла |
Напряжение в узле (кВ) |
Тип узла: 1 – PQ 2 – PU 3 – Uδ |
Выходная активная мощность (МВт) |
Выходная реактивная мощность (МВАр) |
Входная активная мощность (МВт) |
Входная реактивная мощность (МВАр) |
1 |
400 |
2 |
0 |
0 |
1 200 |
0 |
2 |
400 |
1 |
500 |
160 |
0 |
0 |
3 |
400 |
3 |
0 |
0 |
0 |
0 |
4 |
400 |
1 |
300 |
70 |
0 |
0 |
5 |
400 |
1 |
900 |
200 |
0 |
0 |
6 |
400 |
1 |
250 |
40 |
0 |
0 |
7 |
400 |
1 |
200 |
40 |
0 |
0 |
8 |
400 |
2 |
0 |
0 |
1 800 |
0 |
9 |
400 |
1 |
320 |
80 |
0 |
0 |
Для расчета неоходимо знать параметры линии сети. В таблице 3 приведены требуемые параметры в расчете на километр длины линии сети (см. Таблицу 3)
Таблица3. Параметры линии сети на километр
Электрическое сопротивление R (Ом/км) |
Индуктивная реактивность X (Ом/км) |
Емкостная реактивность B (мкС /км) |
0,03 |
0,3 |
3,9 |
Для дальнейших расчетов разделим всю сеть на составляющие ветви (см. Таблица 4).
Таблица 4 – Составляющие ветви сети
Ветвь |
Начальный узел (i) |
Конечный узел (k) |
R (Ом) |
X (Ом) |
B (мкС) |
Длина (км) |
V1 |
1 |
2 |
2,7 |
27 |
351 |
90 |
V2 |
2 |
3 |
2,4 |
24 |
312 |
80 |
V3 |
3 |
4 |
1,5 |
15 |
195 |
50 |
V4 |
4 |
5 |
1,5 |
15 |
195 |
50 |
V5 |
6 |
5 |
4,5 |
45 |
585 |
150 |
V6 |
7 |
6 |
4,5 |
45 |
585 |
150 |
V7 |
9 |
7 |
2,4 |
24 |
312 |
80 |
V8 |
1 |
9 |
2,7 |
27 |
351 |
90 |
V9 |
7 |
8 |
3 |
30 |
390 |
100 |
V10 |
8 |
3 |
8,7 |
87 |
1131 |
290 |
V11 |
1 |
8 |
3 |
30 |
390 |
100 |
V12 |
8 |
5 |
12 |
120 |
1560 |
400 |
Определим соответствующе активные и реактивные мощности в узлах (см. Таблица 5), после чего рассчитаем установившейся режим в узлах сети с передачей по переменному току, см. Таблицу 6.
Рассмотрим биполярную схему с высоковольтной передачей по постоянному току с напряжением ± 500 кВ и с мощностью передачи 2x500 МВт. Указанное значение мощности будем подавать на узел 5 из узла 8, потери мощности на ветке посчитаем на основании (1.12). Сопротивление ветки примем равное 0,03 Ом/км, длина - 400 км. Рассчитаем потери на один полюс, получим:
![]()
Таблица 5. Активные и реактивные мощности в узлах сети с передачей по переменному току
Номер ветви |
Начальный узел (i) |
Конечный узел (k) |
Активная мощность в начале ветки Pi (МВт) |
Реактивная мощность в начале ветки Qi (МВАр) |
Активная мощность в конце ветви Pk (МВт) |
Реактивная мощноть в конце ветви
Qk (МВАр) |
V1 |
1 |
2 |
989,2 |
81,4 |
-972,5 |
30,8 |
V2 |
2 |
3 |
472,5 |
-190,8 |
-468,6 |
181,2 |
V3 |
3 |
4 |
513,8 |
174,3 |
-511,0 |
-176,7 |
V4 |
4 |
5 |
211,0 |
106,7 |
-210,4 |
-130,4 |
V5 |
6 |
5 |
258,7 |
-38,3 |
-256,7 |
-29,5 |
V6 |
7 |
6 |
516,5 |
-10,2 |
-508,7 |
-1,7 |
V7 |
9 |
7 |
87,1 |
-25,6 |
-87,0 |
-21,7 |
V8 |
1 |
9 |
410,0 |
27,9 |
-407,1 |
-54,4 |
V9 |
7 |
8 |
-629,5 |
-8,1 |
637,2 |
23,3 |
V10 |
8 |
3 |
514,4 |
-69,1 |
-500,0 |
32,3 |
V11 |
1 |
8 |
-199,2 |
-7,5 |
199,9 |
-47,4 |
V12 |
8 |
5 |
448,5 |
-45,2 |
-432,9 |
-40,2 |
Таблица 6. Расчетные значения установившегося режима в узлах сети с передачей по переменному току
Номер узла |
Напряжение в узле (1=400 kB) |
Фазовый угол δ |
Баланс активной мощности (МВт) |
Баланс реактивной мощности (МВАр) |
1 |
1,00 |
14,0 |
1 200,0 |
101,8 |
2 |
0,98 |
4,2 |
-500,0 |
-160,0 |
3 |
1,00 |
0,0 |
- 454,8 |
387,8 |
4 |
0,98 |
-2,7 |
-300,0 |
-70,0 |
5 |
0,97 |
-3,8 |
-900,0 |
-200,0 |
6 |
0,97 |
0,6 |
-250,0 |
-40,0 |
7 |
0,99 |
9,3 |
-200 |
-40,0 |
8 |
1,00 |
16,2 |
1 8000 |
138,4 |
9 |
0,99 |
10,0 |
-320,0 |
-80,0 |
Соответственно, в биполярной схеме, с двумя полюсами потери составят 24 МВт. Согласно расчетам потерь в узел 5 мощность будет подана величиной 1000–24=976 МВт.
Остальные параметры данной сети помещены в таблицу 7, как из нее следует, все параметры двух систем одинаковые за исключением трех величин: входной активной и реактивной мощностей в узле 5, выходной активной мощности в узле 8. Следовательно, преобразователь прибавляет в направлении узла 50 МВАр (см. Таблицу 7).
Таблица 7. Значения узловых данных в сети с передачей по постоянному току
Номер узла |
Напряжение в узле (кВ) |
Тип узла: 1 – PQ 2 – PU 3 – Uδ |
Выходная активная мощность (МВт) |
Выходная реактивная мощность (МВАр) |
Входная активная мощность (МВт) |
Входная реактивная мощность (МВАр) |
1 |
400 |
2 |
0 |
0 |
1 200 |
0 |
2 |
400 |
1 |
500 |
160 |
0 |
0 |
3 |
400 |
3 |
0 |
0 |
0 |
0 |
4 |
400 |
1 |
300 |
70 |
0 |
0 |
5 |
400 |
1 |
900 |
200 |
976 |
50 |
6 |
400 |
1 |
250 |
40 |
0 |
0 |
7 |
400 |
1 |
200 |
40 |
0 |
0 |
8 |
400 |
2 |
1 000 |
0 |
1 800 |
0 |
9 |
400 |
1 |
320 |
80 |
0 |
0 |
Таблица 8. Активные и реактивные мощности в узлах сети с передачей по постоянному току
Номер ветви |
Начальный узел (i) |
Конечный узел (k) |
Активная мощность в начале ветки Pi (МВт) |
Реактивная мощность в начале ветки Qi (МВАр) |
Активная мощность в конце ветви Pk (МВт) |
Реактивная мощноть в конце ветви
Qk (МВАр) |
V1 |
1 |
2 |
812,8 |
53,1 |
-801,5 |
4,3 |
V2 |
2 |
3 |
301,5 |
-164,3 |
-299,8 |
132,5 |
V3 |
3 |
4 |
163,2 |
99,2 |
-162,8 |
-126,3 |
V4 |
4 |
5 |
-137,2 |
56,3 |
137,4 |
-84,3 |
V5 |
6 |
5 |
61,6 |
-24,1 |
-61,4 |
-65,7 |
V6 |
7 |
6 |
314,3 |
-48,1 |
-311,5 |
-15,9 |
V7 |
9 |
7 |
78,4 |
-54,1 |
-78,3 |
5,9 |
V8 |
1 |
9 |
401,1 |
-2,5 |
-398,4 |
-25,9 |
V9 |
7 |
8 |
-436,1 |
2,2 |
439,7 |
-28,0 |
V10 |
8 |
3 |
346,4 |
-92,2 |
-339,9 |
-23,5 |
V11 |
1 |
8 |
-13,9 |
-29,8 |
13,9 |
-32,6 |
V12 |
8 |
5 |
1000,0 |
0,0 |
-976,0 |
-50,0 |
Таблица 9. Расчетные значения установившегося режима в узлах сети с передачей по постоянному току
Номер узла |
Напряжение в узле (1=400 kB) |
Фазовый угол δ |
Баланс активной мощности (МВт) |
Баланс реактивной мощности (МВАр) |
1 |
1,00 |
10,7 |
1 200,0 |
20,8 |
2 |
0,98 |
2,7 |
-500,0 |
-160,0 |
3 |
1,00 |
0,0 |
- 476,5 |
208,1 |
4 |
0,99 |
-0,8 |
-300,0 |
-70,0 |
5 |
0,98 |
0,0 |
76,0 |
-150,0 |
6 |
0,99 |
0,9 |
-250,0 |
-40,0 |
7 |
0,99 |
6,1 |
-200 |
-40,0 |
8 |
1,00 |
10,9 |
800 |
-152,7 |
9 |
0,99 |
6,8 |
-320,0 |
-80,0 |
Как видно из вышеприведенных таблиц данного примера (Таблица 5 - Таблица 8; Таблица 6 - Таблица 9), напряжения и значения фазовых углов в узлах сети, после замены ветви с передачей по переменному току – на ветвь с передачей по постоянному току, стали меньше различаться между собой, а, следовательно система приближается к идеальному варианту, когда во всех узлах одинаковое напряжение, 400 кВ, т. е. отсутствуют потери. Кроме того такая замена ветви привела к разгрузке сети по мощности, а именно, до узлов мощность доходит такая же как и в случае с передачей по переменному току, а нагрузка на провода ниже. Таким образом, сетями с передачей электроэнергии по постоянному току можно переносить больше мощности при меньшей нагрузке на сеть.
Список литературы:
1. Acha E., et al.: „FACTS Modeling and Simulation in Power Networks“, John Willey, England , 2004, ISBN 0-470-85271-2.
2. Acha E., et al.: „Power Electronic Control in Electrical Systems“, Newnes Press,
Oxford , 2002, ISBN 0-7506-5126-1.
3. Křivka V.: „Stejnosměrné přenosy v elektroenergetice“, Praha, 2010
дипломов


Оставить комментарий