Статья опубликована в рамках: VII Международной научно-практической конференции ««Проба пера» ЕСТЕСТВЕННЫЕ И МАТЕМАТИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 07 мая 2013 г.)
Наука: Математика
Секция: Геометрия
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
МАТЕМАТИЧЕСКИЕ МЕТОДЫ РЕШЕНИЯ ПРИКЛАДНЫХ ЗАДАЧ В КРИМИНАЛИСТИКЕ И СУДЕБНОЙ ЭКСПЕРТИЗЕ
Коврига Валерий
8 «б» класс, МОУ «Сосновская СОШ» Таврического муниципального района Омской области
Мартынова Надежда Николаевна
научный руководитель,? учитель математики высшей категории МОУ «Сосновская СОШ» Таврического муниципального района Омской области
Барабаш Пётр Григорьевич
Научный консультант майор полиции, эксперт-криминалист ОМВД России по Таврическому району
Введение. Актуальность темы
В современных условиях России экономическая, правовая и социально-психологическая адаптация выпускников к условиям взрослой жизни становится объективной необходимостью. Проблема выбора професcии всегда стоит перед выпускником, а значит интересно знать какие школьные предметы и где могут тебе пригодиться. Например: какое значение информатика и математика имеют для юриста? Во-первых, на современном этапе развития юридической науки увеличивается объем нормативно-правовой, криминологической, уголовно-статистической и другой информации. Особую актуальность приобретает математический анализ разнообразных правовых явлений и процессов, так как развитие экономических, социальных, правовых и иных систем общества должно изучаться с математической точностью. Во-вторых, все эти системы, явления и процессы обладают и количественной мерой. В-третьих, в юридических действиях возникают проблемы оптимизации труда, которые могут быть решены с привлечением разнообразных математических методов. В-четвертых, в математике как раз есть такие понятия как множество, подмножество, функция, распознавание образов, «дерево целей», операция, критерий оптимальности, модель которые используются для обработки информации. Поэтому я сформулировал цель своей работы: показать практическое применение математического аппарата в криминалистике и судебной экспертизе. И для её достижения сформулировал задачи:
1. изучить историю применения математических методов в судебном деле;
2. рассмотреть конкретные физико-математические методы решения прикладных задач в криминалистике и судебной экспертизе;
3. исследовать реальные ситуации, возникающие в судебной практике;
4. выполнить практические работы по измерительной фотографии и плановой съёмке,
5. исследовать реальные ситуации, возникающие в судебной практике;
6. выполнить практические работы по измерительной фотографии и плановой съёмке.
Объектами исследования стали материалы судебной экспертизы и криминалистики, а предметом исследования — задачи, возникающие в ходе судебной экспертизы. Изучив имеющуюся литературу и проанализировав её, собрав материал по теме, выполнив практические работы, я и достиг поставленной цели.
Основная часть
I. Из истории применения математических методов в криминалистике
Криминалистика как наука, разрабатывающая систему специальных приемов, методов и средств собирания, исследования, использования и оценки судебных доказательств, возникла в конце XIX — начале ХХ вв. Судебной экспертизой называются исследования, проводимые согласно процессуальному законодательству, для установления по материалам уголовного или гражданского дела фактических данных и обстоятельств. В начале XIX века в различных странах начинается систематический сбор уголовной статистики: в России в 1802 году организовано Министерство и сбор данных по его работе, в Америке в 1829 г. вышел первый сборник судебной статистики, российский философ Радищев А.Н. писатель, юрист и статистик в своей работе «О законоположении» приходит к важным выводам о роли уголовной статистики. Он предлагает и разрабатывает конструктивную методику статического наблюдения. В 30 годы XIX века во Франции впервые появилось понятие «Моральной статистики». Утверждалось, что задача статистики заключается в том, чтобы выявить и изучить законы общественного развития, которые не менее точны, чем законы природы, а такие общественные явления как рождаемость, смертность, преступность подчиняются определённым статистическим закономерностям. Георг фон Майер (1841—1925) предлагает подсчитывать экономический ущерб, нанесённый преступными действиями, особенно имущественными преступлениями. В 1954 году состоянием уголовной статистики начинает заниматься Интерпол (Международная организация уголовной полиции) и в 1977 году ООН осуществляет первый учёт преступности.
Во второй половине XX века обосновывается применимость математических методов (в том числе и вероятностно-статистических) в различных видах судебной экспертизы: почерковедческой, дактилоскопической, судебно-медицинской. В 70-е годы совершенствуется криминалистическая тактика, разрабатывается система «трафаретов», т. е. разрабатываются определённые алгоритмы действий. Развивается фоноскопия при анализе и синтезе речевых сигналов. При расследовании пожаров применяются графические и геометрические методы [5].
II. Применение математических методов.
Арифметические и геометрические прогрессии применяются при расчетах в задачах, содержащих последовательности взаимосвязанных показателей и объектов (например «финансовые пирамиды»), арифметические (доли, проценты, пропорции) в простых вычислениях в различных сферах правовой деятельности. При оценке правовых ситуаций, связанных с определением истинности или ложности информации, используют логические законы, с расчетами, связанными с величинами и процессами случайного характера (например, при выдвижении версий, при проведении экспертиз), используются вероятностные методы, а метод статистических испытаний (метод Монте-Карло) применяют при расчетах, связанных с величинами и процессами случайного характера, на основе искусственно произведенных статистических материалов (например, при моделировании сложных систем, таких, как управление уличным движением) [3].
III. Геометрические методы в решении прикладных задач
Наибольшее применение в криминалистике, особенно в криминалистской технике, изучающей технические средства и методы работы с вещественными доказательствами, нашли геометрические методы. Эти методы позволяют точно зафиксировать материальные следы преступлений и получить о них количественную информацию. Наличие в уголовном деле точных данных о размерах определённых объектов и их частей, а также о расстояниях между предметами обстановки места происшествия даёт возможность успешно анализировать вещественные доказательства с целью выяснения их роли в процессе подготовки к преступлению, при его совершении и сокрытии следов. Часто в решении практических задач используется положения из тригонометрии, Многие важные для расследования вопросы выясняются с помощью тригонометрических функций острого угла.
В криминалистике применяются измерительные геометрические методы и методы аналитической геометрии, представляющие собой комбинацию из элементарной алгебры и геометрии, методы проективной геометрии.
Обращаться к геометрическим методам при решении прикладных задач приходится при проведении различных построений и расчётов, особенно в судебной измерительной фотографии. При решении геометрических задач применяются такие понятия как подобие треугольников, равенство треугольников, теорема Пифагора, тригонометрические функции острого угла треугольника, объёмы геометрических тел. Из аналитических методов применяются формулы скорости, пути. Из статистических методов формулы нахождения вероятности определённых событий.
Рассмотрим решение некоторых задач [1].
Задача 1. При выстреле из огнестрельного оружия под углом α к преграде 1 пулевая пробоина имеет форму эллипса. Определить угол выстрела α по отношению к преграде по форме пулевого отверстия и известным величинам большой оси эллипса D и малой оси d. Выстрел был произведён орудием, оставив рану d = 9 мм, а пробоина имела размер по горизонтали D = 14 мм. Определить калибр орудия.

Рисунок 1.
Решение.
Вероятно, величина малой оси эллипса равна калибру ствола огнестрельного оружия. Если рассмотрим треугольник ABC, то длина катета AB равна величине малой оси эллипса.
Из таблиц — это крупнокалиберное оружие, ![]() =
=![]() =
=![]() = 0,6428,
= 0,6428, ![]() = 40°.
= 40°.
Задача 2. Гражданину Петрову был нанесён смертельный удар в область сердца. Специалисту необходимо предварительно установить вид холодного оружия, которым было совершено преступление.
Надо определить ширину клинка холодного оружия по повреждению. Длина пореза AB= 32,5 мм, угол под которым клинок вошёл в преграду 45![]() .
.

Рисунок 2.
Решение.
Для этого надо измерить глубину раневого канала на теле, а также угол, под которым был нанесён удар. Надо определить ширину клинка холодного оружия по повреждению. Длина пореза AB= 32,5 мм, угол под которым клинок 45۫![]() . Углы
. Углы ![]() и ß равны как вертикальные. В ∆ABO AB=32,5 мм,
и ß равны как вертикальные. В ∆ABO AB=32,5 мм, ![]() ß =45
ß =45![]() .
. ![]() =
=![]() , АО=АВ∙
, АО=АВ∙![]() =32,5∙
=32,5∙![]() = 22,75
= 22,75![]() 23 мм. Ширина клинка 23 мм.
23 мм. Ширина клинка 23 мм.
Задача 3. При решении некоторых криминалистических задач приходится определять параметры геометрических объектов. Например: Определить объём украденного перевезённого песка, если он находится на территории склада предпринимателя N.

Рсунок 3.
Решение.
Куча песка с точки зрения математика имеет форму конуса. Воспользуемся формулой объёма конуса V=![]() Sh, где S — площадь основания конуса, а h — высота его. Так как основание конуса является окружностью, то её площадь вычислим по формуле S=
Sh, где S — площадь основания конуса, а h — высота его. Так как основание конуса является окружностью, то её площадь вычислим по формуле S=![]() .
.
Воспользуемся формулой объёма конуса V=![]() Sh, где S — площадь основания конуса, а h — высота его. Так как основание конуса является окружнос-тью, то её площадь вычислим по формуле S=
Sh, где S — площадь основания конуса, а h — высота его. Так как основание конуса является окружнос-тью, то её площадь вычислим по формуле S=![]() . Радиус конуса вычислим по формуле r=
. Радиус конуса вычислим по формуле r=![]() , где C — длина окружности, которую можно непосредственно измерить. Измерим дважды образующую конуса, для более точного результата. Итак, С — 16,5 м AC= АВ= 3 м , BD=r 6,5:6,28=2,6 м.
, где C — длина окружности, которую можно непосредственно измерить. Измерим дважды образующую конуса, для более точного результата. Итак, С — 16,5 м AC= АВ= 3 м , BD=r 6,5:6,28=2,6 м.
Высоту h конуса вычислим по теореме Пифагора.
h=![]() =
= ![]()
![]() 1,5 м. Подставим найденные значения и получим объём украденного песка.
1,5 м. Подставим найденные значения и получим объём украденного песка.
V=![]() Sh, V=
Sh, V=![]() 21,23·1,5=10,61 м. Плотность песка равна 1,3 т/куб. м.
21,23·1,5=10,61 м. Плотность песка равна 1,3 т/куб. м.
Зная плотность песка, вычислим его вес. M=V![]() М=10,61·1,3
М=10,61·1,3![]() .
.
Задача 4. Групповым признаком канала ствола гладкоствольного оружия является его диаметр. При выстреле на дроби формируется след в виде сегмента дуги окружности высотой h=1,2 мм и шириной l=9 мм., который соответствует радиусу внутренней части канала ствола R. Рассчитать величину радиуса R по известным значениям h и l.
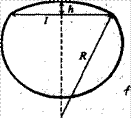
Рисунок 4.
Решение.
Рассмотрим прямоугольный треугольник на чертеже для окружности радиуса R и применим теорему Пифагора, получим выражение
![]() .Раскроем скобки и выразим из выражения R, получим R=
.Раскроем скобки и выразим из выражения R, получим R=![]() мм. Подставим данные задачи в эту формулу. Получим
мм. Подставим данные задачи в эту формулу. Получим
R=![]() =10 мм. Тогда диаметр ствола будет 20 мм.
=10 мм. Тогда диаметр ствола будет 20 мм.
Такая задача решается с целью определения калибра снаряда по осколкам при проведении взрывотехнических экспертиз.
Практическая работа «Методы проективной геометрии при определении действительных размеров объекта по фотоснимку.
Цель нашей работы была освоить методику определения действительных размеров объектов по фотоснимкам, выполненным по правилам измерительной фотографии перспективно-наклонным и перспективно-горизонтальным методом. Фотоснимки, выполненные измерительным способом, отличаются тем, что в них заключена возможность их использования в процессе расследования в качестве источника информации. Способы получения информации базируются на законах геометрической оптики, знаниях из начертательной геометрии и теории перспективы.
1. Практическая работа «Методы проективной геометрии при определении действительных размеров объекта по фотоснимку».
Цель нашей работы была освоить методику определения действительных размеров объектов по фотоснимкам, выполненным по правилам измерительной фотографии перспективно-наклонным и перспективно-горизонтальным методом. Фотоснимки, выполненные измерительным способом, отличаются тем, что в них заключена возможность их использования в процессе расследования в качестве источника информации.
Способы получения информации базируются на законах геометрической оптики, знаниях из начертательной геометрии и теории перспективы.
Плановая съёмка. На снимке используется предмет, который имеет фиксированные размеры, например коробок спичек.
По отношению размеров предметов на снимке, составляем пропорцию.


Рисунок 5.
Выполнив измерения на снимке, получили: длина коробки спичек — 7 мм
Длина ножа 32 мм. Настоящая длина коробки спичек — 50 мм. ![]() =
=![]() , Х
, Х![]() 230 мм=23 см. Найденная длина ножа 23 см, что соответствует действительности. Согласно консультации эксперт-криминалиста в этом случае необходимо делать запрос на спичечную фабрику о размерах коробка, поэтому большей частью применяют простую линейку, которую кладут параллельно предмету.
230 мм=23 см. Найденная длина ножа 23 см, что соответствует действительности. Согласно консультации эксперт-криминалиста в этом случае необходимо делать запрос на спичечную фабрику о размерах коробка, поэтому большей частью применяют простую линейку, которую кладут параллельно предмету.
2. Проведение фотосъёмки и определение действительных размеров объектов по фотоснимку.
2.1.Перспективно-горизонтальный фотоснимок. Этот снимок применяется при измерительной фотосъёмке с глубинным и квадратным масштабом. Для этого на снимке используется метрический квадрат со стороной 1 метр, разделённый на квадраты шахматной доски. Метрический квадрат располагают строго по центру кадра, так, чтобы его ближняя сторона совпала с нижним краем снимка. При наличии такого квадрата, проведя несложные геометрические построения, можно по снимку определить размеры предметов и их взаимное расположение.
Изображение системы перспективных координат на перспективно-горизонтальном снимке: hh1 — линия горизонта, D и D1 точки пересечения продолжения диагоналей метрического квадрата. Главная точка P совпадает с геометрическим центром фотоснимка, полученного с полного негатива.
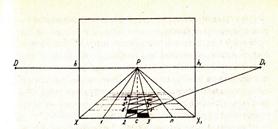
Рисунок 6.
На перспективно-наклонном снимке точка Р будет находиться за пределами снимка, а в остальном построение системы перспективных координат аналогично [1].
2.2.Схема построения размеров предметов по фотоснимку, выполненному с метрическим квадратом.
Так нами были вычислены размеры ёлки и ножа, видимых на снимке.

Рисунок 7.
Нанесём на фотографию систему перспективных координат. Наша фотография получилась в перспективно-наклонном виде. Точка Р1 находится за снимком и она является для данного случая главной точкой. Линия горизонта DD1. В данной координатной системе найдём высоту модели ёлки, её диаметр.
1. KN=7 см,
Составим для решения задачи пропорцию
KN: сторону квадрата на снимке (ближайшую горизонтальную) = высота ёлки: метрический размер стороны квадрата 6,8:8,2=Х:100;
Х=6,8·100:8,2=83 см. это фактическая высота ёлки.
2. диаметр ёлки d. На чертеже это 2 см. Составим пропорцию
2:8,2=d:100 d=2·100:8,2=24 см. отсюда радиус основания ёлки 12 см.
3. На фоторгафии нож. Найдём АВ из ![]() ABС,
ABС, ![]() ABС — прямоугольный, АВ — гипотенуза, АС=2,5 см ВС=0,6 см.
ABС — прямоугольный, АВ — гипотенуза, АС=2,5 см ВС=0,6 см.
АСфакт=2,5·100:12=21 см
ВСфакт.=0,6·100:5=12 см
![]() =
=![]() =
=![]() =
=![]()
![]() 24 см
24 см
Высота ёлки и длина ножа совпадают с настоящими размерами.
Выводы.
Задачи, поставленные в работе, выполнены. В работе сделан обзорный перечень различных математических методов. Из всего разнообразия математических методов, применяемых в криминалистике и судебной экспертизе, более полно рассмотрены геометрические. Проведены практические работы, которые помогли лучше усвоить методы измеряемой фотографии. При разборе задач использовалась конкретная ситуация. Работа может быть интересна тем, кто собирается стать юристом, судебным экспертом, следователем или просто участковым полицейским, а также она знакомит учащихся с применением математики в жизни.
Список литературы:
1.Курин А.А. Элективный курс «Физика и математика. Решение прикладных задач в криминалистике и судебной экспертизе» Волгоград. 2008 г. — 128 с.
2.Перельман Я.И. Занимательная геометрия. Екатеринбург. 1994 г. Тезис, 1994. — 288 с.
3.Рассолов М.М., Чубукова С.Г., Элькин В.Д. Элементы высшей математики для юристов: учеб. Пособие. Издательство: ЮРИСТЪ, 1999. — 184 c. (дата обращения 18.01.2013) [Электронный ресурс] — Режим доступа. — URL: http://www.bars-insk.narod.ru›stud/VM/lecture0.htm- . (дата обращения 16.01.2013).
4.Селиванов Н.А. Математические методы в собирании и исследовании доказательств. М. Юридическая литература. 1974 г.,1974. — С. 9—21, 51—53, 59—63.
дипломов

Комментарии (3)
Оставить комментарий